Using BBQ Skewers to Calculate Pi (Order out of Chaos)

This is a little experiment anyone can do to illustrate the underlying order that can arise out of random events. Strictly speaking it's a study in probability theory. But more generally it can be used to show how complex events in nature can be describe with mathematics. This aspect of our Universe has both puzzled and amazed people at least as far back as ancient Greece. I personally find it astonishing that the underlying laws of nature lend themselves to a mathematical description.
With this easy to do experiment, you can throw a bunch of BBQ skewers on the floor repeatedly and, by looking at their random behavior, calculate pi.
Buffon's Needle
The math behind this experiment was introduced back in the 18th century by Georges-Louis Leclerc, Comte de Buffon. The question he posed and then studied was this;
If we throw a needle onto a floor made of parallel strips, each the same width, what is the probability that the needle will lie across a line between two strips?
If you are really interested in the full mathematical treatment of this problem, there are many places online where it exists. The part of the derivation that interests us is that the probability that the needle lies across a line is given by this equation;

The important part is that pi appears in the result, so that by measuring all the other variables, pi can be calculated. Rearranging the above equation gives;
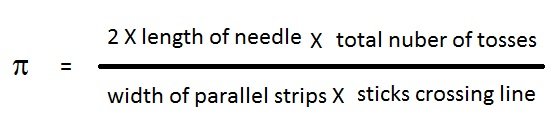
The Set Up
In practice, you can pick any needle length and any width for the parallel lines, but to simplify the calculation, you can make these two lengths equal, so that they cancel in the equation. There is also nothing magical about using a needle and a floor, any stiff object and flat surface with parallel lines will do. I chose BBQ skewers and my floor. Since my floor is made up of squares, I simply ignored the short vertical lines and used only the longer parallel lines to define the width of the strips. This picture highlights the setup;

You can either toss one stick at a time and keep track of the total number of sticks tossed and the number that cross a line. Or, to speed things up you can toss many sticks at a time and keep track that way. I chose to toss 10 at a time. One such toss, where 6 out of 10 sticks cross the parallel lines, is shown here.

The Results
The following graph summarizes my results for estimating pi using this exercise.
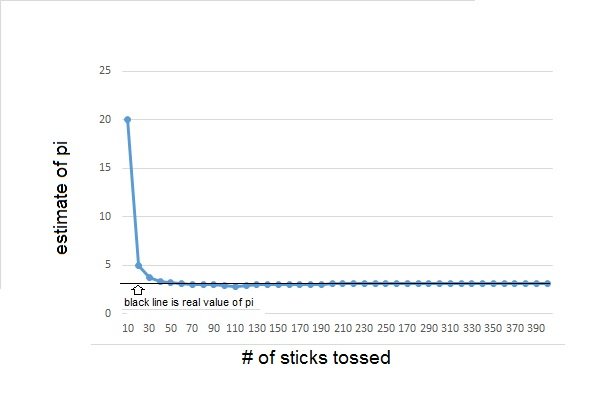
Notice that the estimate gets better as the number of tosses increases. This is the nature of probabilistic events. Namely that the estimate to the true probability becomes more accurate the more trials are done. You can see from the graph that, as the number of tosses increases, the estimate of pi gets more accurate. I threw 10 skewers at a time a total of 40 times, representing 400 sticks being tossed. This didn't take as long as it sounds, and you can see that the result is already converging on the value of pi. In fact, to make the graph, I calculated an estimate for pi each time I tossed the 10 skewers and I hit the value of pi to two decimal places 4 times, the first one being at 270 sticks tossed.
The more you toss the more accurate your estimate of pi will be. You don't have to do the tosses all at once either. You can do this for a bit every now and then and keep a running tally. Try it and see to how many decimals you can get your value of pi to agree with the real value. How many tosses does it take you to get the value accurate to that that many decimal places? Try different length of sticks. You can play around with this in many ways.
Hey @spalser, great post! I am a relatively new Steemer and recently joined. It would be great if you would check out my latest post and click follow if my content interests you. Much appreciated!
Great one. Critical thinking require critical mind