Elements of Set Theory: Ordered Pairs
Elements of Set Theory: Ordered Pairs
Consider the following pair set:
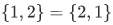 this can be thought as an unordered pair.
this can be thought as an unordered pair.
Consider another pair set with additional information:
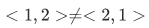 , where 1 is the first component, 2 is the second component.
, where 1 is the first component, 2 is the second component.
What do we want from this?
What we want is to define a set that uniquely encodes both what x and y are, and also what order they are in. In such a way that if I have this equation,
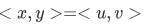
This would imply that 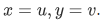 .
.
How would we state this definition?
Let's consider first some definition that lacks our desired property.
- If we define our ordered pair as
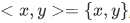 , then
, then 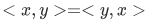 since
since 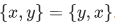 . So this is not the definition we're looking.
. So this is not the definition we're looking. - Consider this definition
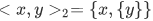 . Again the desired property fails, since
. Again the desired property fails, since 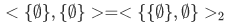 , both sides being equal to
, both sides being equal to 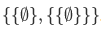 .
.
The first successful definition of an ordered pair set was given by Norbert Wiener in 1914, who proposed to let,
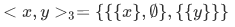
A simpler definition was given by Kazimierz Kuratowski in 1921, and is the definition in general use today:
Definition <x,y> is defined to be 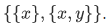 .
.
We must prove that this definition captures the property that the ordered 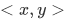 uniquely determines both what x and y are, and the order upon them.
uniquely determines both what x and y are, and the order upon them.
Theorem 3A 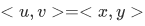 iff
iff  .
.
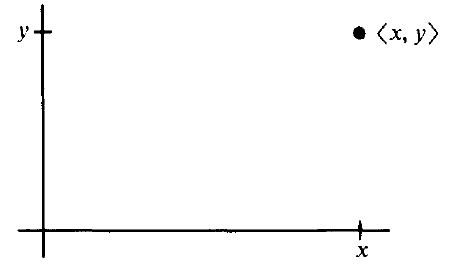
Now suppose that we have two sets A and B, and we form ordered pairs 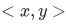 with
with 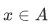 and
and  . The collection of all such pairs is called the Cartesian product
. The collection of all such pairs is called the Cartesian product 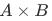 of A and B.
of A and B.
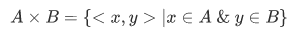
The strategy to show that
 is a set runs as follows.
is a set runs as follows.
- If we can find a set that already contains all of the pairs
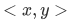 we want, then we can use a subset axiom to cut things down to . A suitable large set to start with is provided by the next lemma.
we want, then we can use a subset axiom to cut things down to . A suitable large set to start with is provided by the next lemma.
Lemma 3B If 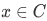 and
and 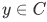 , then
, then 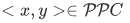
Proof: The fact that the braces 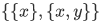 are nested to a depth of 2 is responsible for the two applications of the power set operation;
are nested to a depth of 2 is responsible for the two applications of the power set operation;
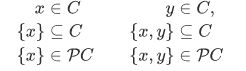
Then we have,
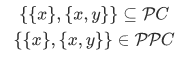
Corollary 3C For any sets A and B, there is a set whose members are exactly the pairs 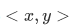 with
with  .
.
Proof: From a subset axiom we can construct
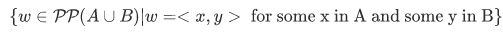
This corollary justifies our earlier definition of the Cartesian product 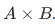 .
.
Disclaimer: this is a summary of section 3.1 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora
Thank you for reading ...


You got a 11.63% upvote from @nado.bot courtesy of @sinbad989!
Send at least 0.1 SBD to participate in bid and get upvote of 0%-100% with full voting power.