OK, so the answers which suggest 98 all find a plausible pattern. But it has a couple problems: the sequence cannot be continued backwards, and there is no obvious reason for 64 to be the starting point either of the sequence or of the diagram.

The closest we can come to a predecessor for 64 using the "add the sum of digits" rules is:

64 - 9 = 55 (digit sum 10)
64 - 10 = 54 (9)
64 - 11 = 53 (8)
64 - 15 = 49 (13)
64 - 16 = 48 (12)

But what if the numbers actually form a cycle? What happens if we plot them as radial coordinates, evenly spaced?

ListPolarPlot[{{Pi/3,74},{0,85}, {-2*Pi/3,115},{- Pi,122},{2*Pi/3,64}},PlotRange->All, Joined->True]

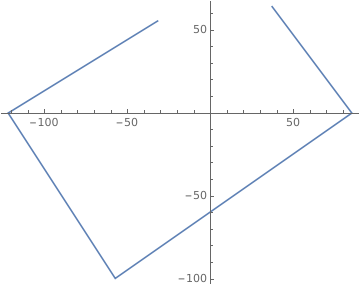
Obviously, they form points on a rectangle and we should fill in the missing point so that this pattern is maintained.

50 looks about right, but the line going from (0,85) to (-2*pi/3,115) in polar coordinates has equation

r cos t - (19 * sqrt*3 / 23) * r sin t - 85 = 0

At t = -pi/3 we have r = 398/8 = 48.875, which I submit as my answer.

(All of the above is, I should add, quite tongue-in-cheek.)