Welcome to the World of the Fourier Transform - Fourier Analysis
Hello friends, in this publication I will explain a very important metamatical science content, I refer to how to proceed with an analysis of fourier, without good as some know the Fourier transform is one of the most important mathematical expressions that already exist that this allows us to pass a signal to the frequency domain to obtain information that is not evident in the temporal domain, for example, it is easier to know what bandwidth the energy of a signal is concentrated by analyzing in the frequency domain. Today in this publication will clarify many doubts about the Fourier series, I invite you to observe this quality content. For greater understanding as the explanation is made, a series of exercises are developed, in such a way that the explanation is much more complete.
Welcome to the world of the Fourier Transform!
FOURIER ANALYSIS
Any function of a variable x defined between the limits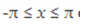 
that is repeated periodically and that has a finite number of discontinuities can be represented by a FOURIER SERIES..
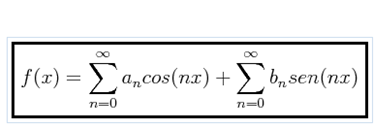
Taking the term corresponding to = 0 out of the summation we have the following alternate representation :
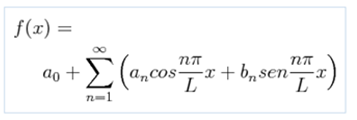
The coefficients an and bn can be obtained from the following relationships:
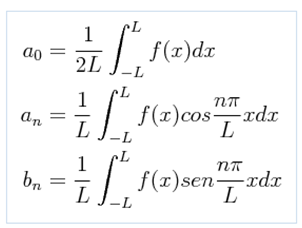
If f (x) is a function in the time domain, that is f (x) = f (t), the expansion by means of Fourier series allows us to convert any function of the time domain to the frequency domain in which the periodic function does not is represented according to the way in which it varies with time but according to the infinite sum of a fundamental frequency and its harmonic frequencies (multiples integers of the fundamental frequency) of which are shown below some that correspond to a frequency of 60 Hertz (60 cycles per second):
){kind=link}
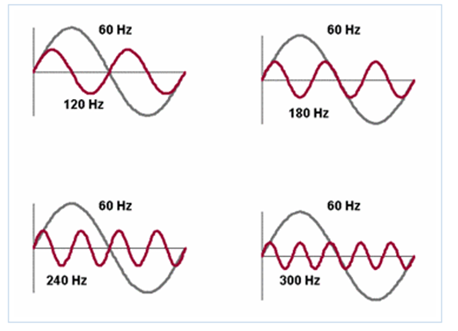
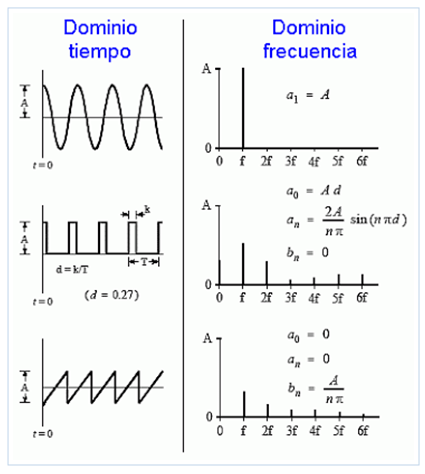
The amplitudes of the harmonics depend on the wave that will be reconstructed from this infinite sum of frequencies. As we usually do a giagram to visualize the way in which a periodic traveling wave varies with time, we can also make a diagram in the frequency domain to visualize the spectrum of frequencies that the traveling wave reproduces in the time domain:
){kind=link}
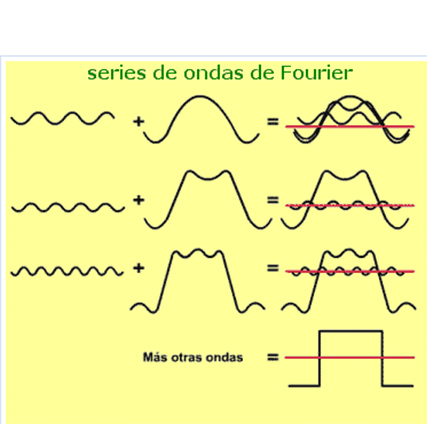
In the following diagram we have as the sum of the fundamental frequency and some harmonics approximate the reconstruction of a square wave:
){kind=link}
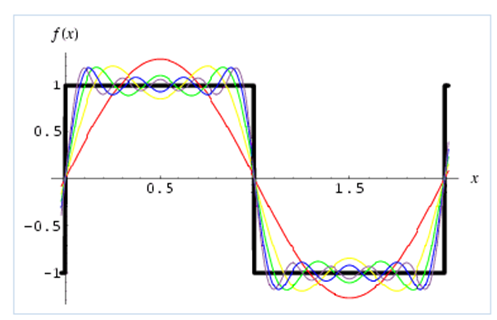
Naturally, between more and more harmonics we add to the fundamental frequency, the greater the approximation of the reconstructed wave in the time domain:
){kind=link}
There is a good reason why the expansion of a periodic Fourier series function is possible. Before going into detail, we will define what orthogonal functions are. It says that two functions f (x) and g (x) defined within a range a < x < b are orthogonal if they meet the following condition:
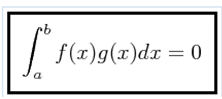
PROBLEM: Determine if the following functions are orthogonal:
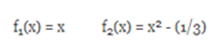
Using the orthogonality condition of two functions, we have the following for these two functions:
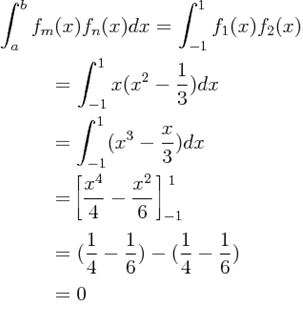
It is concluded that the two functions are orthogonal.
Returning to the Fourier series, if we look at the following set of basic functions:
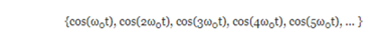
we will discover that:
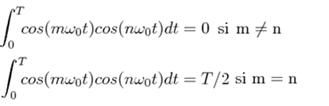
Based on this, we can see that the functions 1, cos (wot), cos (2wot), cos (3wot), etc., which correspond to the expansion in Fourier series form a set of orthogonal functions. Similarly, for the set:
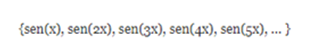
we have :
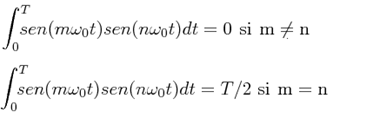
Without much thought, we can see that any of the components of a set of basic functions is independent of the others in the vector sense, as are the basic unit vectors:
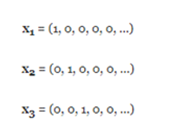
The orthogonality of the basic functions is precisely what allows us to carry out the expansion. If it were not for this orthogonality, the Fourier series would not be possible.
Time after Jean-Baptiste Fourier discovered his famous infinite trigonometric series that allow to represent almost any type of periodic function, other series were discovered with which one could also achieve the same but without the harmonic trigonometric terms. One such series uses the polynomials known as the Legendre polynomials, of which the first polynomials are:
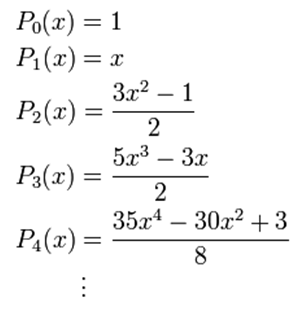
Like the Fourier series, representations based on Legendre series are infinite series.
The mathematical property that allows to use the Legendre polynomials for the representation of a periodic function is the same property that allows the Fourier series to achieve the same effect, the orthogonality of the terms. We can verify in the terms given above that all the terms are orthogonal under the following operation:
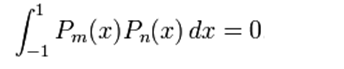
Another type of series is what we can achieve through the Laguerre polynomials, of which the first polynomials are:
In addition to the Fourier series, the Legendre series and the Leguerre series, there are many other possible series with which we can represent any function that is repeated periodically. In fact, the possibilities of representation are endless. All that is required of a series is that the functions used as terms of said series are orthogonal, which, incidentally, allows them to be grouped and accommodated in a vectorial representation.
We will now define what a normalized function is. Unlike the orthogonal functions whose definition rests on the product of two different basic functions, the normalized function is differed over the product of the function with itself in the following way:
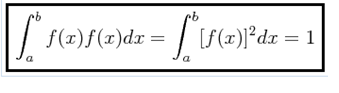
When a function is not normalized, the previous definition can be used to normalize it.
When we have a serial expansion for which we use base functions that in addition to being orthogonal have been normalized, we call these orthogonal functions.
The expansion in series to be used will depend on the specific nature of the problem that is being analyzed, although in some cases certain problems take us directly to the series that solves them. However, the Fourier series has an advantage over other series: it allows us to convert a function from the time domain to the frequency domain as we saw above, so that the expansion lends itself to an intuitive analysis, which is not feasible when we carry out an expansion by means of polynomials.
In general, if we have a complete set of orthonormal functions:
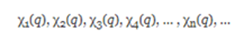
we can carry out an expansion of a function f (q) in terms of these orthonormal functions:
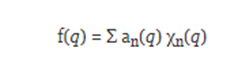
We have seen how to represent a periodic function by expanding it into an infinite series of terms. But is it possible to represent something that is not a newspaper in this way? . The answer is a resounding no. However, we can represent something that is not periodic if we resort to a limiting process by which the infinite series can be replaced with an integral one.
Consider the following train of pulses in which each pulse is repeated every T seconds:
){kind=link}
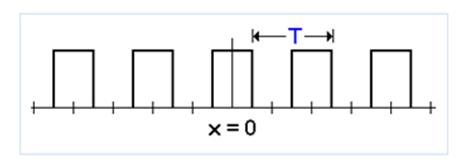
Suppose now that without varying the width of each pulse we stretch the distance between them increasing the period of the wave until T acquires an infinite value:
){kind=link}
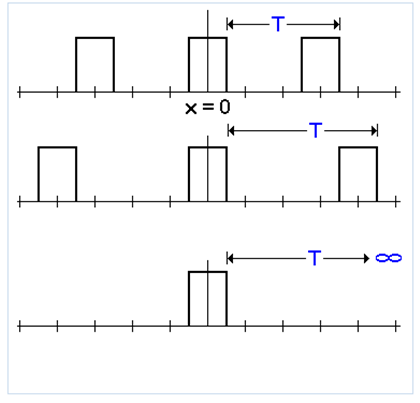
When carrying out this process, we will discover through the evaluation of each series that as we carry out this process increasing the period of the signal the Fourier spectral components (in the graph that corresponds to the frequency domain) are getting closer and closer, until that in a moment what seemed a series of clearly distinguishable vertical lines seems to be taking on the appearance of something dense in which we can no longer see the individual lines, then we have a graph, in the frequency domain, that shows us precisely for a train of pulses two steps in this decompaction process going from a period T = 1 to a period T = 5:
){kind=link}
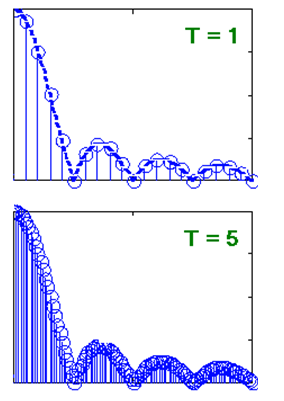
In the final step we have a single isolated pulse, what we already have is a curve (formed by the heights of an infinite number of spectral lines sharpened at an infinitely small distance from each other), in which case we do not already speak of a a Fourier series but a Fourier transform.
In the following diagram we have the effect on the spectrum of frequencies to be extended over a period of pulse elperido of time T between each pulse keeping the duration of each pulse constant (from top to bottom), extend the width of the pulse maintaining the T period of time constant (from left to right), and expand both parameters (as is customary in the technical literature, each frequency spectrum has been drawn both for positive values of the frequency and for negative values of the same, which it can be done from the mathematical point of view without any problem):
){kind=link}
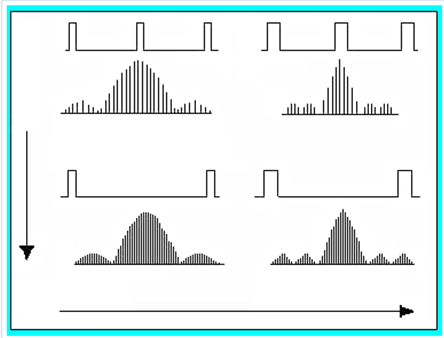
The effect that interests us is that by which we increase the period of the wave in such a way that we are able to obtain an isolated pulse.
In the following problem we obtain the frequency spectrum, as a function of the wave number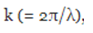 
, for the periodic pulse that we have just described.
PROBLEM: Obtain the Fourier transform of a specified wave function in the following way:
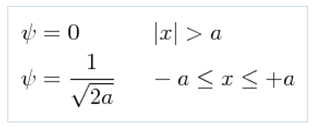
Using the definition of the Fourier transform we have the following:
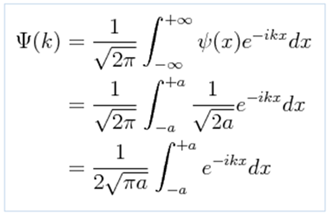
In order to carry out the integration, we make a change of variables:
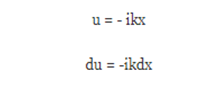
With this we have then:
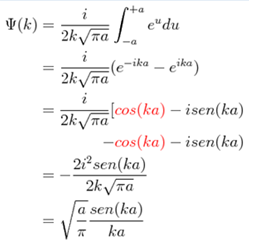
References Bibliography :
-http://hyperphysics.phy-astr.gsu.edu/hbase/Audio/fourier.html
http://reference.wolfram.com/language/guide/FourierAnalysis.html
Elias Stein and Guido Weiss, Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, 1971.
Elias Stein with Timothy S. Murphy, Real Harmonic Analysis - Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton University Press, 1993.
Elias Stein, Topics in Harmonic Analysis Related to the Littlewood-Paley, Princeton University Press, 1970.
Yitzhak Katznelson, An introduction to harmonic analysis, Third edition, Cambridge University Press, 2004.
Yurii. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhauser 1988.