Introduction to Machine Learning: Training Neural Networks!
Introduction to Machine Learning:
Training Neural Networks
Linear models and What is Machine Learning:
https://steemit.com/mathematics/@jackeown/introduction-to-machine-learning-introduction-and-linear-models
What is a Neural Network:
https://steemit.com/mathematics/@jackeown/introduction-to-machine-learning-the-neural-network
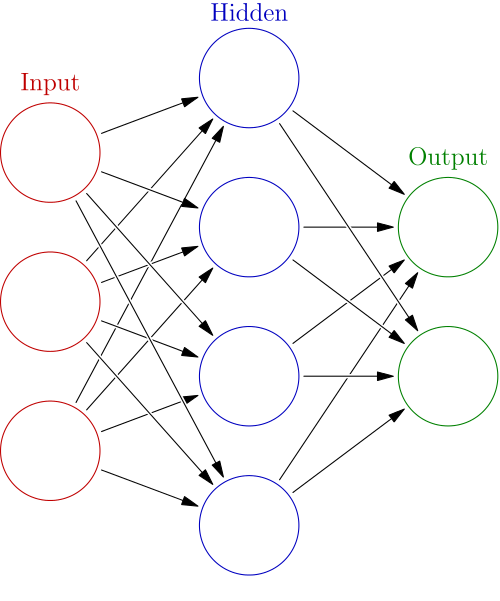
As I (tried to) explain in my previous post, a neural network is a model whose output is determined by variables on the edges and neurons. Each neuron has a "bias" variable and each edge has a "weight" variable. The output of a neuron is determined as some activation function (we'll use the sigmoid) applied to the weighted sum of its inputs plus the bias term for that neuron. This can be seen as the following equation where wx is the dot product of the vector of weights and the vector of input. (In other words wx is just the weighted sum of the inputs)
f(x) = sigmoid(wx+b)
Now that we see what each neuron outputs in terms of its weights and biases, we can consider how to make the network compute what we want. The weights and biases are called "parameters" of our model. A specific set of weights and biases corresponds to a particular hypothesis. We can start with a "random" hypothesis by having small random weights and biases and then we slowly change them in order to get a better accuracy. One way to do this is through a process called gradient descent...
Gradient Descent
In the first post in this series I talked about how you can use the parameters of a model to turn the task of learning into an optimization problem. This means that we can look at error as a function of parameter values (in our case weights and biases). Given a set of training data pairs (Xi,Yi) we can compute the "error" or "cost" in a few ways but the most common (and simplest) is referred to as "mean squared error" which is exactly what it sounds like. Let us define the output of our neural network when fed Xj to be "Pj" Our error is the average of the difference between Pi and Yi squared for all i. (mean squared error)
If we substitute all of our weights and biases in to replace Pi, then we get a (very long and complicated) equation for cost in terms of our inputs, weights, biases, and outputs.
By holding the inputs and outputs constant, we can take the partial derivative of our error with respect to the weights and biases!
(This is a calculus concept and it's very important, but if you don't know about derivatives, it's just the "rate of change"...so this tells us "how error changes when we change weights and biases".)
The vector of all of these derivatives is called the gradient and it is very special. In our "parameter space", it describes the direction of steepest ascent. (The direction to move all parameters to maximize error locally). The direction of steepest DESCENT is then just the opposite direction and we can take a little step in that direction! The following picture describes this idea:
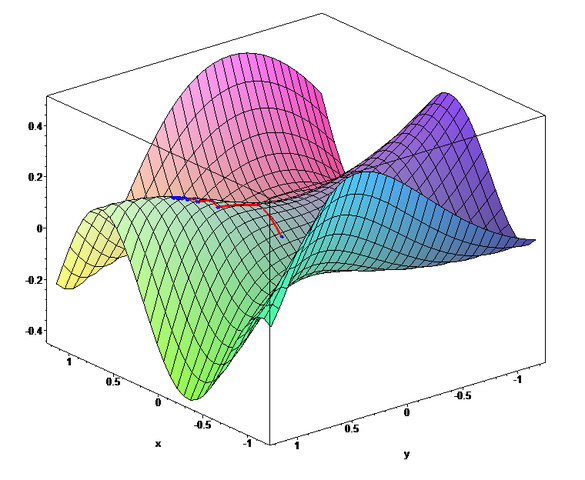
(The red line traces from left to right the path of gradient descent in a two parameter optimization problem.)
Now we can also do "stochastic" gradient descent, where for each step we compute the error based on a small random sample or "batch" from our data instead of computing it using ALL our data. This is much more efficient, but can result in going "back and forth" in parameter space if your samples happen to be chosen poorly or if the "batch size" is too small.
Extra credit: Daniel Shiffman's gradient descent video!
This guy has great videos mostly on quick programming projects which he does mostly using Processing.js
Next I hope to talk about evolutionary approaches to optimization!
I'd love suggestions on future directions for posts on Machine Learning and let me know what I can do to improve!
Thanks,
JacKeown ;)
I found out about Daniel Shiffman's video by serendipity following up on your first post, helped demystify what you were talking about by a great deal.
I think you should consider some adding some exercises to these to help with user engagement and really learning what you're talking about.
I find machine learning a very interesting area. I just found your machine learning posts, do you plan on making some implementation? As in coding a neural network
Yeah I might go through an example using python and numpy showing how processing neural networks can be represented as matrix multiplication.
Nice, I'm waiting for it. :)
I tried to go through a neural network example, but got confused trying to understand parts of it...but you should check out my post with good resources for learning:
https://steemit.com/programming/@jackeown/introduction-to-machine-learning-sample-code-and-other-resources
The first link is an 11-line neural network in python with numpy (basically what I planned on writing anyway ;))