Last tutorial, I explained how the binomial expansion formula was derived, and I stated at the end of the tutorial that worked examples will be posted so as to know the advantage of the formulae.
Have you read the previous tutorial? If no, click this below link.
Deriving of binomial expansion formula for two variables (a+b)^n

Now, let's get started.

By considering this below examples,

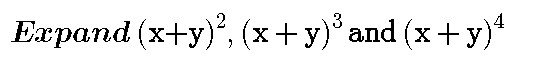
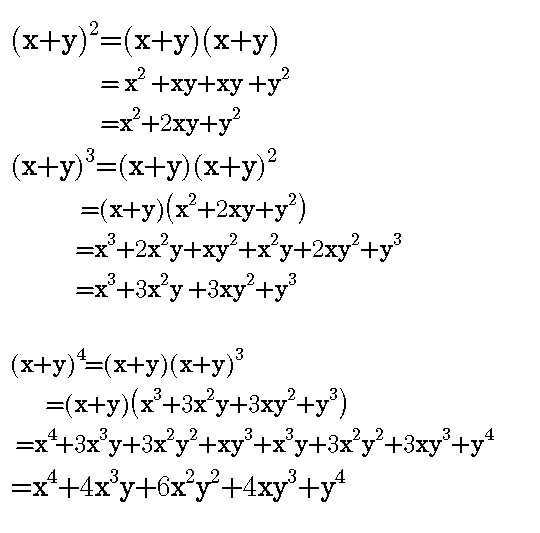
You can see that it is more complicated when we are expanding for the power of 4, let's assumes you see a contest on Steemit which the price is 2000SBD and you are given a question to expand for a power of 10 and you are given just 3minutes.

How will you do it?

Will you do it like we did in above examples?

This is where we will apply binomial expansion formula

Let's use binomial expansion formula to expand (x+y)^4 and you will know which is faster between the two methods.

Recall the formula of binomial expansion

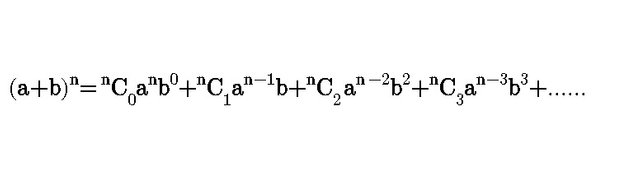
By comparing (x+y)^4 with the formula,

a=x , b=y and n=4

Substituting all the values to the formula, then we have,

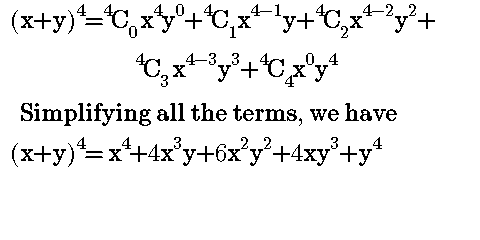
Now, which method will you apply for the contest question now?

There are some tricky questions also like expand (x - 2y)^3, the reason I bring up this kind of example is just to avoid doing mistake since we are dealing with questions with positive in all the questions that we have solved.

What we need to do is to compare it with binomial expansion formula,

a=x , b= -2y and n=3

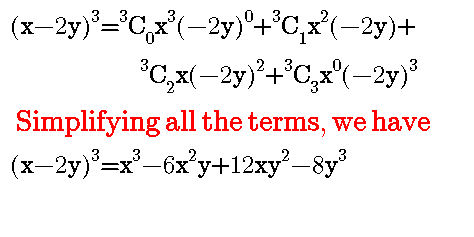
I couldn't be able to solve more examples because I'm using phone to type.

Always visit my blog for more tutorials on mathematics.

Reference

John Bird Engineering mathematics

You can also read my previous tutorials:
Deriving of binomial expansion formula for two variables (a+b)^n
Easy method to derive binomial expansion formula
Tutorial on Combination
Explanation on why 0!=1

Pictures: All equations were written with maths editor.

Follow @hayzeed and resteem this post.