You are viewing a single comment's thread from:
RE: Are there more points on a line or in a square? - Intresting bits of mathematics - week -2
I always thought a point had a position but an infinitesimal size and a line segment had a way to specify the segment (start/end positions or other) but an infinitesimal width. Either way, that means there's an infinite number of points on a line segment and an infinite number of points (and line segments) in a square.
Yeah, but there are different sizes of infinities - for example there isn't a 1 to 1 mapping from the integers to the real numbers, so there are more real numbers than integers - however there is a 1 to 1 mapping from the integers to the rational numbers, so there are the same number of integers as there are fractions. The question is really is the infinity of points that makes up the square larger than the infinity of points that makes up the line. Thanks for reading!
Yes. I realise that and it is helpful to think about different sizes of infinities. My favourite example that is easier to grok is the comparison between the set of natural numbers and the set of even numbers. That's like thinking from the inside - it works by looking at the members of the set. From the outside of the set infinite is infinite and since infinite is not a quantity then the set sizes are not comparable. Right now though I think we're talking about some finer points of theory that don't particularly matter outside of any particular application.
So, yes, we can use the intuition that although the number of points on a line segment are infinite, and the number of line segments in a square are also infinite, there are more points in a square. By extension the number of squares in a cube is infinite.... that leads to the number of points in shapes of various dimensions:
1D: inf (e.g. points on a line segment)
2D: inf^inf (points on a square)
3D: inf^inf^inf (points in a cube)
4D: inf^inf^inf^inf (points in a 4D hypercube)
etc....
If your definition is more restrictive for how the shapes go into the higher dimensions, such as it must be an exact slice of the higher dimensional shape and they must be packed without overlaps, then the density chnges somewhat. First what do I mean by an exact, non-overlapping slice, a row of points on a line segement. Then a row (or column) of equal length line segments that extend from edge to edge of the square... (extend into higher dimensions). Then the density of points increases proportional to the number of dimensions:
1D: inf
2D: inf^2
3D: inf^3
4D: inf^4
This is fun stuff btw :)
One of the main points about what I was writing was sort of to get across how unintuitive it is. The set I wrote at the end sort of generalises to higher dimensions so if you let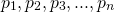 be the first n prime numers just to avoid factors and perfect squares and consider the set
be the first n prime numers just to avoid factors and perfect squares and consider the set
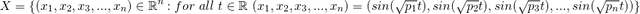
then you have lots of functions going between -1 and 1 that are always out of phase as proved above with the irrational number bit, so they will produce every combination of n numbers between -1 and 1 and hence cover any n dimensional square/cube/ whatever you call it in higher dimensions. This is a mapping from the real numbers to that square. If you can't read the maths then try downloading the image