Reciprocal Trigonometric Functions On Right Angled Triangles
Hi everyone. This math post features reciprocal trigonometric functions on right angled triangles. This is a follow up post on my post on right angled triangles and SOH CAH TOA.
Math text in the form of images done in LaTeX and QuickLaTeX.com.

Topics
- Review Of Sine, Cosine, Tangent Functions & SOH CHA TOA
- The Reciprocal Trigonometric Functions
- Trying To Memorize The Reciprocal Trigonometric Functions
- An Example
Review Of Sine, Cosine, Tangent Functions & SOH CAH TOA
With the sine, cosine and tangent trigonometric functions, you can find side lengths and/or angles inside right angle triangles. The SOH CAH TOA memory aid is helpful for memorization.
Sine Of An Angle (SOH)
The sine of an angle is given by the side length opposite to x divided by the side length of the hypotenuse. Remember that the hypotenuse is the longest side of the right angle triangle and it is opposite to the right angle.

Cosine Of An Angle (CAH)
The cosine of an angle x is given by the side length adjacent (next to) to x divided by the side length of the hypotenuse.
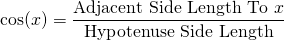
Tangent Of An Angle (TOA)
The tangent of an angle x is the ratio of the opposite side length divided by the side length of the adjacent side to x. The hyptenuse is not involved in the tangent of an angle.
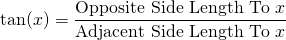
The Reciprocal Trigonometric Functions
Reciprocal trigonometric functions are an extension to SOH CAH TOA. If we have the ratios/fractions in SOH CAH TOA flipped, we have the recipocal trigonometric functions.
Reciprocal Of Sine: Cosecant
The cosecant of an angle x is the length of the hypotenuse divided by the opposite side length to the angle x.
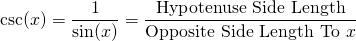
Reciprocal Of Cosine: Secant
The secant of an angle x is the reciprocal of the cosine function. It is the ratio of the
hypotenuse length divided by the adjacent side length to the angle x.
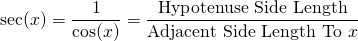
Reciprocal Of Tangent: Cotangent
The secant of an angle x is the reciprocal of the cosine function. It is the ratio of the
hypotenuse length divided by the adjacent side length to the angle x.
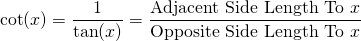
Trying To Memorize The Reciprocal Trigonometric Functions
Trying to memorize the cosecant, secant and cotangent functions can be tricky. You could use SOH CAH TOA and take its reciprocals to obtain SHO CHA TAO.
How I remember these is first associating cotangent with tangent. The sine function goes with cosecant which starts with a different first letter other than s. The secant function goes with the cosine function where the first letters are different.
An Example
This example will be based on this image. The reference angle is 37 degrees.

With SOH CAH TOA, the sine, cosine and tangent of 37 degrees can be found.

Once the sine, cosine and tangent ratios are determined, you can find the respective recirpocal trigonometric ratios.

One could try this example again but with 53 degrees instead as an exercise. The ratios should evaluate to the same value.

excellent explanation friend greetings already voted