Multiplying Binomials, The FOIL Method & Another Way Of Multiplying Two Numbers
The previous post was about multiplying two numbers/quantities together with the distributive law. This post will be based on multiplying two binomials together and the FOIL method.
Suppose you have an expression such as:
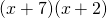
This could be expanded with the FOIL method. The two x's are multiplied together which is added by x times the 2 plus the 7 times the second x plus 7 times 2. In math notation, it will look like this. FOIL stands for first, outer, inner and last.
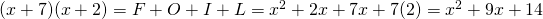
In general, if we have four different numbers a, b, c and d, (a + b)(c + d) would be equal to:
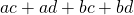
A Memory Aid
Another way to look at the FOIL method is through a memory aid image.
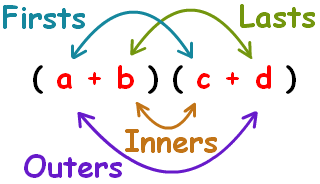
An Alternate Way Of The FOIL Method
This alternate way involves splitting each of the two numbers into two smaller numbers. Instead of multiplying something scary such as 27 times 11, you can use the FOIL method on (15 + 12)(5 + 6).
Example One
Multiplying 27 and 11 with the FOIL method gives
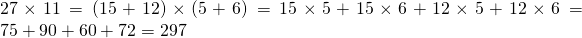
An alternate way with this example would be to split the 11 only to obtain 27(10 + 1) = 270 + 27.
Example Two
What is 14 x 18?
With the FOIL method in mind, we have:
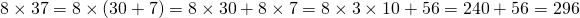
You could skip the one step if you know that 8 x 30 = 240 right away.
Example Three
Here is one more example. What is 13 x 38?
The first two examples involved all addition. Subtraction can be used as well. You could use 38 as 30 + 8 but another option would be 38 = 40 - 2
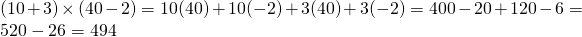
Extension
A natural extension would be an increased number of terms. Instead of something like (a + b)(c + d), you could have (a + b)(c + d + e) or more.
For the (a + b)(c + d + e) case, the expansion of it would be:
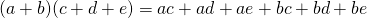
The math text was from the QuickLaTeX (lay-tech) website. LaTeX is not possible in Markdown but I work around it with images.