The Fundamental Theorem of Arithmetic, Its Implications, and Some cryptography
The Fundamental Theorem of Arithmetic
In my previous post, I wrote a proof of the infinity of prime numbers, but I nonchalantly hand-waved a very important detail, that every integer greater than 1 has a prime divisor. This is actually part of a more important theorem in mathematics, called the fundamental theorem of arithmetic-- which we will abbreviate henceforth as FToA. So just for completion, I'll talk about it here in this post, although I will not be proving it here since we'll need a lot of background lemmas than I'm comfortable of working with in a single post . I will instead talk about its depth, and also discuss the importance and the usefulness of the FToA. We state it formally here:
Fundamental Theorem of Arithmetic. Every integer greater than 1 has a unique list of prime factors (divisors), along with their multiplicities.
What does it mean?
So what does this actually mean? To understand it better, let's take a relatively small integer greater than 1 that we can work with, let's say 48, it's prime factors (or divisors, they are the same) are 2 and _3 _ since 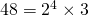 , the theorem says then if we list the prime factors of 48, it will appear as
, the theorem says then if we list the prime factors of 48, it will appear as 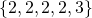 , noting that the prime 2 has multiplicity four, that is, it appears four times in the prime factorization
, noting that the prime 2 has multiplicity four, that is, it appears four times in the prime factorization 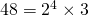 of 48 (see that exponent 4 up there?). The theorem says that the list
of 48 (see that exponent 4 up there?). The theorem says that the list 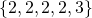 of the prime factors of 48 is unique, this means that we will never ever find any other list of primes, such that if we multiply them together we will get 48. Also, just to emphasize, the multiplicity (again, it's just the number of times a prime appears in the factorization of an integer) of the prime factor is important, to see this, consider the prime factorization of 6, which is
of the prime factors of 48 is unique, this means that we will never ever find any other list of primes, such that if we multiply them together we will get 48. Also, just to emphasize, the multiplicity (again, it's just the number of times a prime appears in the factorization of an integer) of the prime factor is important, to see this, consider the prime factorization of 6, which is 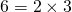 , hence its list of prime factors is
, hence its list of prime factors is 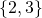 , so we see that while 48 and 6 have the same prime factors, namely, 2 and 3 , they still have different list of prime factors if we take in to account multiplicities.
, so we see that while 48 and 6 have the same prime factors, namely, 2 and 3 , they still have different list of prime factors if we take in to account multiplicities.
Why is it important?
The FToA is important because it made us understand that, in a way, the primes are the building blocks of numbers, it tells us that we can always break down any whole number into prime factors, and conversely, the prime numbers can create any whole number by multiplication. Also, as a by product, the FToA allows us to make statements like: "if n is an integer, let p be a prime divisor of n..." since we know prime divisors always exist, and being able to conjure these kinds of statements can be really handy when we want to prove some property of a number.
What about the number 1?
1 is not prime. Well, to elaborate why, let us look at the defining characteristic of number 1-- for any number n, 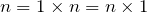 , that is, multiplying any number by 1 gives you back the same number. This is not a good thing, if we consider 1 prime, then FToA will fail, in particular, the uniqueness of the prime factorization will fail. Let's take 48 again, since
, that is, multiplying any number by 1 gives you back the same number. This is not a good thing, if we consider 1 prime, then FToA will fail, in particular, the uniqueness of the prime factorization will fail. Let's take 48 again, since
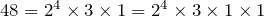 , then we have two different lists of prime factorization of 48. In fact, we can just keep multiplying by 1 to end up with an infinite lists of prime factorization. This is pretty much the same reason why, in the statement of the FToA, we have " ...for every integer greater than 1", because 1 is not prime, and it cannot be divided by any other positive number besides itself.
, then we have two different lists of prime factorization of 48. In fact, we can just keep multiplying by 1 to end up with an infinite lists of prime factorization. This is pretty much the same reason why, in the statement of the FToA, we have " ...for every integer greater than 1", because 1 is not prime, and it cannot be divided by any other positive number besides itself.

Some Cryptography
The study of integers, or whole numbers is called number theory, and a few years ago, it was considered as the "purest" field of mathematics, in that, it has no immediate application to the real world. Some mathematicians of the past were pretty smug about this fact-- until cryptography came. Number theory, in particular, integer factorization into primes is one of the main tools used in cryptography to secure information. Now, my knowledge about cryptography and computer science is pretty sparse in general, but I hope I get this right. Let's try to mention some useful terms first, encryption and decryption. Encryption is the process of encoding information or data (also called plaintext) into nonsense (also called ciphertext), at least for the unintended party, and decryption is the exact opposite of this. We're going to discuss about asymmetric systems here, and we need one more important term, a key. In asymmetric cryptographic systems, one can think of the public key as an information you feed to the encryption machine along with the plaintext to make the ciphertext, similarly, the private key is the information you feed to the decryption machine to convert ciphertext back to plaintext. In symmetrical systems, the public and private keys are the same, but this is not the case for asymmetric systems. In this system, the keys are numbers, and the private key, that only you know, are, ideally, two large prime numbers p and q. The public key then, is their product 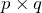 .
.
We segue a little bit to some computer science; when you have a relatively large number, you can design an algorithm to find its prime factors, for a simple example of this algorithm you can make a program or function that takes any whole number, say, again, 48. When your program runs, it will start dividing 48 by 2, check if the quotient is an integer, if it is, you put it into some list, so you have 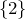 , you take the quotient again, 24, and keep dividing it by 2 and putting the 2 on the list until eventually you have a quotient that is no longer divisible by 2. You repeat this process with the next prime 3, and then again to the next prime 5, and so on until you have the full list of its prime factors. Turns out these kinds of factoring algorithm make really large number factorization intractable because your computer would have to run for years before it'll spit an answer. That, along with the fact that we still do not have a full information of the distribution of primes make factorization algorithms seemingly complex. To summarize, it's very easy to multiply prime numbers, but it's a lot harder to find the prime factors that make up a number.
, you take the quotient again, 24, and keep dividing it by 2 and putting the 2 on the list until eventually you have a quotient that is no longer divisible by 2. You repeat this process with the next prime 3, and then again to the next prime 5, and so on until you have the full list of its prime factors. Turns out these kinds of factoring algorithm make really large number factorization intractable because your computer would have to run for years before it'll spit an answer. That, along with the fact that we still do not have a full information of the distribution of primes make factorization algorithms seemingly complex. To summarize, it's very easy to multiply prime numbers, but it's a lot harder to find the prime factors that make up a number.
So, to end this, we'll do a simple demonstration of using prime numbers to public and private keys to secure an information. Let's say Bob, who has a private key using the two primes (283,293) that he chose before hand, asks Alice: "Alice, tell me your Birthdate, use the public key: 82919." Now, Alice will encrypt her birthdate in an encryption machine using the public key 82919. Alice's encrypted information might be available for all to see, along with the public key, but anybody else who wants to peer in to the decrypted information would have to factor out 82919, and we know that's not a very easy feat. But Bob, who knows before hand that 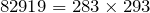 , can easily decrypt the message using his own private key. In summary, this kind of asymmetric cryptographic system is useful for one-way communications in which the recipient and sender doesn't have to agree in advance what the key is (like agreeing on a "code name").
, can easily decrypt the message using his own private key. In summary, this kind of asymmetric cryptographic system is useful for one-way communications in which the recipient and sender doesn't have to agree in advance what the key is (like agreeing on a "code name").
That's it for today, I hope you learned something from this post.
Edit: For most of the stuff here, I just cross-checked with their respective wikipedia articles, especially about FToA, for this post, here are my references:
FToA
Cryptography
Nice Stackoverflow thread about the importance of primes to cryptography
Complexity of factorization algorithms
Congratulations @blackiris! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP@originalworks
@originalworks :)
You should add some references, as this is a decent intro into basic cryptography
To be honest, I'm not very confident in my knowledge of cryptography. The only books that I've read that are actually related to the topic are books on Elliptic Curves.
Hey everyone starts from somewhere.
My start into cryptography was with ciphers and codes, that progressed to encryption, hashing, etc and so forth. But I like this post,