[Let's learn math #3] Sandwich Theorem and solving problems on it...
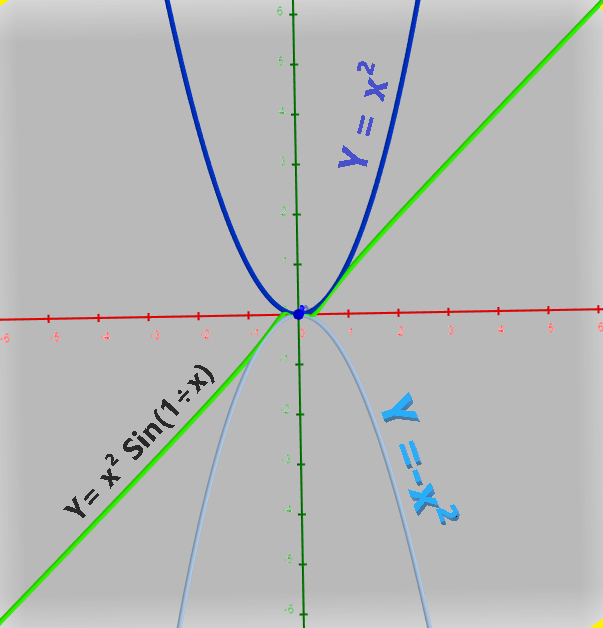
Basic Introduction of Sandwich theorem
Sandwich theorem, also called as Squeeze principle is an important theorem to find the limit of a function (which can't find directly or simple methods ) via comparing the function with two other functions whose limits are known or can be calculated easily.This theorem is very useful and also very important in field of Calculus and real analysis.
Sandwich theorem was used for the first time by mathematicians Archimedes and Eudoxus to compute the value of .gif) . But later on Carl Friedrich Gauss gave modern version of Sandwich theorem.
. But later on Carl Friedrich Gauss gave modern version of Sandwich theorem.
Sandwich theorem or Squeeze principle is also called as Pinching theorem, Sandwich rule, Squeeze lemma and two Policeman and a drunk theorem..
Definition of Sandwich Theorem
Let .gif)
.gif) and
and .gif) be three functions such that:-
be three functions such that:-
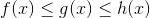
for all x near a or possibly at a see graph below:-
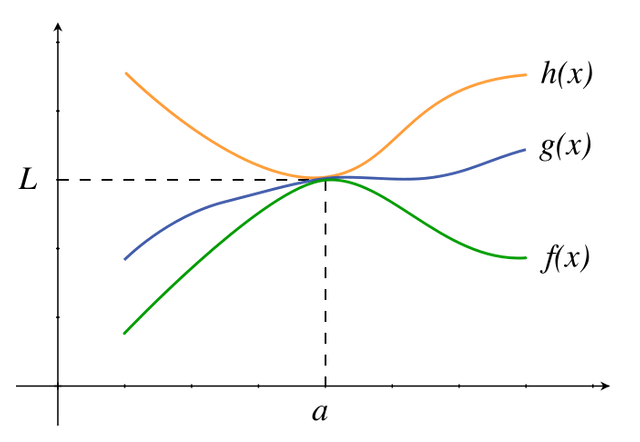
And also it is given that:-
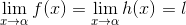.gif)
Then by Sandwich theorem:-
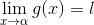.gif)
This theorem is also applicable in sequence, which is as follows:-
If
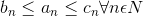.gif)
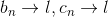.gif) , then
, then 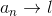.gif)
Proof of Sandwich Theorem
We have given that:-
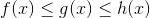 -----(1)
-----(1)Also
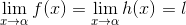.gif)
Then by using the definition of limit we have i.e given .gif) >0 ,however small there exists
>0 ,however small there exists .gif) ,
,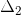.gif) belongs to set of real numbers such that :-
belongs to set of real numbers such that :-
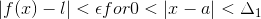.gif) and
and 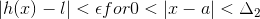.gif)
Let
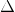.gif) = maximum of (
= maximum of (.gif) ,
,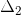.gif) )
)Then we have:-
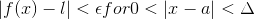.gif) and
and 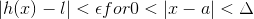.gif)
Now by using the property of modulus we can say that:-
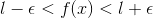.gif) if
if 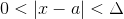.gif) ___(2)
___(2)and
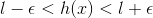.gif) if
if 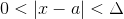.gif) ___(3)
___(3)Therefore from (1),(2) and (3) we get:-
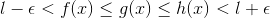.gif) if
if 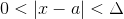.gif)
Which implies
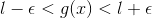.gif) if
if 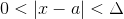.gif)
Which implies
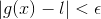.gif) if
if 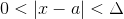.gif)
Therefore,
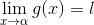.gif)
Hence Proved....
How to use Sandwich theorem in functions
In order to solve the various problems using Sandwich theorem, follow the following steps:-
- Write the given function...
For example,
Question:1)
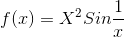.gif)
- Then by using some property of given function, try to make two other functions whose limits are same as follows:-
For example,in this case the value of
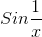.gif) is from [-1,1]
is from [-1,1]i.e.
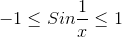.gif)
Now multiply both sides by .gif) we get :-
we get :-
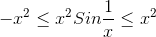.gif)
Now as x approaches to zero, .gif) and -
and -.gif) will become zero in other words, we can say that:-
will become zero in other words, we can say that:-
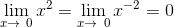.gif)
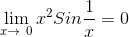.gif)
Lets do some more questions
Question:2) Prove that:-
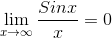
Solution:- Let
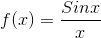.gif)
Now we know that value of Sinx always lies between [-1,1] , therefore we can say that:-
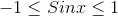.gif)
Dividing both sides by x we get:-
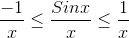.gif)
Now
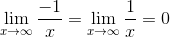.gif)
Therefore, by Sandwich theorem:-
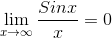
Hence proved....
Question 3):- Prove that:-
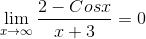.gif)
Solution:- Let
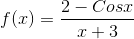.gif)
Now we know that value of Cosx lies between [-1,1] i.e. we have:-
.gif)
On multiplying by -1 we get:-
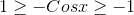.gif)
or
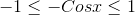.gif)
Now on adding 2 we get :-
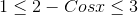.gif)
On dividing whole inequality by x+3 we get :-
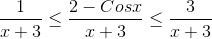.gif)
Since,
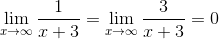.gif)
Therefore, by Sandwich theorem:-
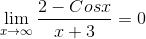.gif)
Hence proved....
Applications of Sandwich Theorem
Sandwich theorem majorly help us in proving the existence and nature of limit of certain functions, which can not be find using common methods.
It also help us to find whether the certain sequence is converges to a limits or not at a given point, by binding the sequence with two other sequences whose convergence is known to us at same point.
Citations:-
(https://en.wikipedia.org/wiki/Squeeze_theorem) (Introduction,definition and proof of sandwich theorem and Question 1)
(https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/squeezedirectory/SqueezePrinciple.html) Question 2 and 3 are taken from here.
(https://www.quora.com/What-are-the-applications-of-sandwich-theorem) Applications of sandwich theorem has taken from here
While all the graphs are made by me by using 3D geogebra and desmos. Also solutions to the problems are my own methods....