The problem and amazing solution of secure cryptographic key exchange
Cryptography is a subject I've been interested in for a long time. I think it started with that movie that runs every Christmas for 24 hours in the States. The main character worked so hard to decrypt that special message.

Since then, knowing that secret messages existed, I've always been fascinated with codes and ciphers and encryption. This technology forms the very backbone of the internet and blockchain technology in general. Securing communications has been a problem for a long time, many governments struggled and still struggle with it today. So I'd like to talk more about Cryptography.
In this article I intend to talk about the main problem with the exchange of encryption keys that existed, who tackled this problem, and what the solution to that problem ended up being. There have been many solutions to this over the decades and people have independently come to similar conclusions, this article is just one such conclusion. So here we go I suppose.
The Problem with exchanging cryptographic keys
The problem with encrypting something like an important message to an ally for example, is that you must not only get the message to the ally but you must also get them the means to decrypt the message. The whole purpose of encryption is that if the encrypted text is intercepted in someway, it doesn't really matter. The intercepting party will not be able to read the message without the key. However, if the party can intercept the message then they surely also have the ability to intercept the key.
Imagine if your will (and if you can because of my bad drawings) that a three letter agency has a box with a lock on it. The lock happens to be red. Lets assume for the sake of argument this box and the lock are impenetrable.
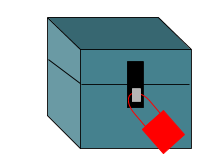
In this box is some very important information about a foreign government. The agency wants to send this information to an allied government but the only way to get this box to the ally is through hostile territory. The agency sends the box to their ally and it gets intercepted. The agency also needs to send a key to the lock to their ally and that too gets intercepted


Now your could put the key in another box but then you'd need to put the key to that box in yet another box and so on. There is no way transport the key openly through hostile territory and expect it to not get intercepted. So what is the solution?
The theory of secure key exchange
To simplify this way down, the answer is to not transport the key openly in the first place. You instead transport the locks.

The ally sends the agency their nice blue lock to use when the agency is sending them important information and the agency sends their ally their nice red lock. The keys are kept by the individual agencies and never sent out into the world and kept private.
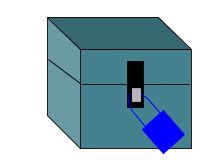
The box is filled with important info locked with the blue lock and sent back to the ally. The ally then sends his blue lock back, unlocked of course.
To speed this up a little, what they could be exchanging is a common key and another lock. This forms the basis of secure key exchange. Lets make this one purple and the box transparent so we know what is inside.
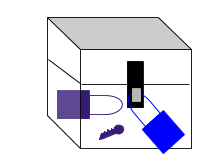
The agency sends a different lock and a copy of the key to their ally. Since the agency has the original key and the ally has a copy of that key, both agencies can unlock the purple lock. This speeds up communication between the groups since it cuts out the need for the return of an unlocked blue lock.
How does this work for real?
The above thought experiment is great, but padlocks can be picked and boxes can be broken. So how does this work in the real world? Maths.

Warning: Do not use any of this to create your own encryption algorithm. Use ones provided by professionals and have gone through vigorous scrutiny. These numbers are too small to provide any protection. This is for demonstration purposes only.
People that are way smarter than I am worked on this issue for a long time. One method to this issue was first published by Whitfield Diffie and Martin Hellman in 1976. They explained a method for secure key exchange using modular arithmetic.
What they came up with was a method using the multiplicative group of integers modulo p, where p is prime, and g is a primitive root modulo p. These two values are chosen in this way to ensure that the resulting shared secret can take on any value from 1 to p–1. Here is an example of the protocol, with secret values in bold. Also I'm going to switch to the classic Bob and Alice names for ease and consistency elsewhere that speaks about encryption.
Alice and Bob first have to agree to a few values for the numbers p and g. It's perfectly fine for these values to be known and intercepted even.
Lets say they agree on p= 23 and g = 5.
Alice chooses a secret integer a = 6, then sends Bob the result of g^a mod p
5^6 mod 23 = 8 (call this result A)
Bob chooses a secret integer b = 15, then sends Alice the result of g^b mod p
5^15 mod 23 = 19 (call this result B)
Alice computes the shared value (call the shared value s) using the result she got from Bob s = B^a mod p
19^6 mod 23 = 2
Bob computes the shared value using the result he got from Alice s = A^b mod p
8^15 mod 23 = 2
Now they have a shared value, the number 2. Note that they did not agree to the number 2, they arrived there after first agreeing upon starting numbers for p and g and computed the shared number. What would an eavesdropper see during this exchange? The original values 23 and 5 and the "encrypted" values 8 and 19. Any further communications will happen with the shared value of 2 using a different algorithm that had already been established prior to the Diffie–Hellman exchange.
The Wrap-up
So to pull this together with my analogy above. 8 is Alice's "lock", 6 is Alice's key. 19 is Bob's "lock", 15 is his key. The algorithm is the box and the shared value 2 is another key inside that box that they will use for a different lock (algorithm) that could be contained inside that box as well or already determined.
Hope you enjoyed and learned a little about how secure key exchange is done. Thanks
--Veemun
Nice graphical explanation!
Thanks!