Mathematics / Arithmetic / Introduction
Welcome to the math classes, today we start with the arithmetic, we will give a small introduction supported with videos where each mathematical property is explained in detail.
Arithmetic is the process of performing certain operations with numbers or variables. There are six closed arithmetic operations; addition, subtraction, multiplication, division, powers and roots.
Addition
1 + 1 = 2
To define the number one is a rather difficult task, but we all have a good intuitive sense of what the "unit" is. The unit is the property of having or thinking of a single amount. For example, think about when you have a dollar, a kilogram of potatoes, or a light year. From here you can recursively define the natural numbers by assigning a new name for each new number of units we have:
1 unit one
2 1 + 1 two
3 1 + 1 + 1 three
⋮ ⋮ ⋮
n 1 + 1 + ... + 1 enes
Now that we have named the numbers we can also define the process of counting the number of units we have. For example,
Subtraction
Subtraction can equally be defined as counting the initial number of units and eliminating a certain amount. For example:
means, having 5 units take away 3 units, leaving a result of 2 units.
Multiplication
Multiplication is an abbreviated form of repeated addition. For example:
- 3 = 15
What this means is to add three five times, or add five three times.
Note that in some regions and cases, it is better to use the symbol of the cross or the letter "x" instead of the point or also *.
Division
Division is the opposite operation to multiplication.
6/3 = 2
The upper division problem asks if six is 1 +1 +1 +1 +1 +1, and three is 1 +1 +1, so in how many sets of three can we separate six? The answer is, of course 2, since
In the division it is the first operation in which a problem arises. In all previously defined operations (addition, subtraction and multiplication) we could perform the operation on any pair of numbers that we chose. However, in the division you can not divide by zero. Much was said about this fact throughout history, and even through his studies in all of mathematics.
The notion of number is one of the most fundamental in mathematics. Its origin goes back to antiquity and through the centuries it has gone through a process of extension and generalization of real numbers.
Introduction to basic operations
In the field of arithmetic, each number has a defined value, so 30 will always be worth thirty, the symbol of the absolute value of a number is represented as follows:
_ | n | being n any whole number, negative or positive_
It should be noted that the value of a number, preceded by the plus sign or the minus sign, will always be the same:
| 3 | = | -3 | = 3
from this it follows that:
| 1 + n | = n
this is because the absolute value indicates the distance on the number line between any number and 0, and whether the number is positive or negative, the distance is the same.
As we have already seen in the classification of quantities, the Rational Numbers, which will be studied in depth in this chapter, are classified as WHOLE and FRACTIONARIES. An integer is, for example, 2, while 0.5 or 1/2 is a fractional number, which can be written in those two ways.
Integer numbers
They are those numbers that indicate an exact amount. Its basic operations are, as in the other types of numbers, addition, subtraction, multiplication, division, enhancement and filiation, this last operation can be applied to a small group of whole numbers, to perfect squares, perfect cubes, etc.
To add or subtract two numbers you have to take into account the signs of them: to add two numbers of equal signs, add their absolute values and leave the sign they have; To add two numbers with different signs, subtract the absolute value of the minor from the absolute value of the largest and leave the sign of the largest number.
For example: -5-3 = -8; 5 + 3 = 8; 5-3 = 2; -5 + 3 = -2
Multiplication is an abbreviated sum, so 3 + 3 + 3 + 3 + 3 can be written and performed as 3x5 = 15.
The division consists of looking for a number that multiplied by the divisor, results in the dividend, this number is called quotient, often the division is not exact and a residue is obtained. Divisions can be reprinted in the following ways:
8/2 = 8 ÷ 2 = 4, because 4x2 = 8, in the same way: 26/13 = 26 ÷ 13 = 2, because 2x13 = 26.
Poefication is an abbreviated multiplication, consisting of two elements: the base, which is the factor that will multiply by itself, and the exponent, which indicates how many times the base will multiply itself: 3x3x3x3 = 3 ^ 4 = 81
Radiation, as stated above, is an operation that can only be applied to certain radicle numbers so that the result remains rational: if a square root is to be applied, the number must be a perfect square; if a cube root is going to be applied, the number must be a perfect cube ... We will explain later how the irrational numbers are simplified.
The result of a radiation is a number that when elevated to the root index, results in the subradical quantity.
√4 = 2; ∛27 = 3, when the root index is 2, it is usually omitted.
Addition of fractions
The addition of fractions is one of the basic operations that can be carried out on fractions.
Addition of homogeneous fractions
Sum of fractions of the same denominator .To add two or more homogeneous fractions, the numerators are added and the common denominator is left.
Addition of heterogeneous fractions: Form 1
The addition of two or more heterogeneous fractions is done as follows:
- The minimum common multiple of the two denominators is calculated.
- The numerators are calculated with the formula: numerator by common denominator and divided by denominator.
- The numerators are added (since the modified fractions have the same denominator).
example :
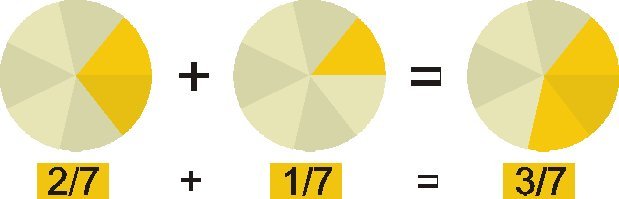
Image source :https://upload.wikimedia.org