Quantum calculus /

Consider any real or complex variables q, and let's take a look at the expression

1 + q + q·q + q·q·q + q·q·q·q + q·q·q·q·q
which can also be written as
1 + q + q^2 + q^3 + q^4 + q^5
Read this as a function in q, i.e. consider the following polynomial, which we'll call "u6"

u6(q) := 1 + q + q^2 + q^3 + q^4 + q^5

This polynomial has an important property, namely that when you plug in q=1, you find the value 6:

u6(1) := 1 + 1 + 1^2 + 1^3 + 1^4 + 1^5 = 1 + 1 + 1 + 1 + 1 + 1 = 6

Here is the graph of the function, u6(q), with q interpreted as real number in the inteveral from -1 and 2.

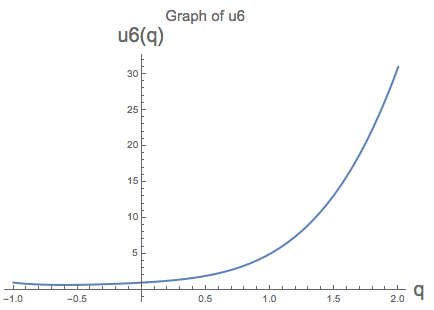
For sure, if you have any non-negative integer k, then q^k at q=1 equals 1^k, which is just 1. For this reason, any polynomial that is the sum n terms of the form q^k, will, at q=1, evaluate to n. For example, consider

u8(q) := 1 + q + q^2 + q^3 + q^4 + q^5 + q^6 + q^7

If fulfulls

u8(1) := 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8

Now, more generally, let's consider a function u(n,q) of two arguments. The first argument shall be an integer, n, and the second any other number, q.

u(n,q) := 1 + q + q^2 + q^3 + .... + q^(n-2) + q^(n-1)

As I hope I've motivated above, this function fulfulls

u(n,1) := 1 + 1 + 1^2 + 1^3 + .... + 1^(n-2) + 1^(n-1) = n

This has a surprising consequence: The arithmetic of natural numbers is embedded in the arithmetic of those functions.

For example, consider the function u(2,q) and u(3,q). Define two new functions, f and s, like so:

f(q) := u(2,q) + u(3,q)

and

s(q) := u(2,q) * u(3,q)

which means

f(q) = (1 + q) + (1 + q + q^2) = 2 + 2·q + q^2

and

s(q) = (1 + q) * (1 + q + q^2) = 1 + 2·q + 2·q^2 + q^3

Because of what's been said before, those two functions are actually just deformations of the numbers five and six. Indeed

f(1) = 2 + 2·1 + 1^2 = 5

and

s(q) = 1 + 2·1 + 2·1^2 + 1^3 = 6

We see that we can abstract away from the natural numbers and works with functions, which secretly at one point know about basic arithmetic. However, at the pint q=3.5, the u's will not look related to the natural numbers and their arithmetic is something much wilder.

---

The most serious application of this concept is in combinatorics of vector spaces. The subject goes by the name of q-analogs and has toy applications in various fields.

You have your q-derivative and the q-integeration and there are literally infinitely other ways to extend the natural numbers in a similar way.

Another variation of this idea goes by the name quantum calculus. Other interesting applications are for deviant definitions of entropy.

In fact, I have some q-analogs that I came up with, one where q doesn't have to be from what is called a field in mathematics (something like the real or complex numbers), that I come back to every now and then.
Let me know if particular aspects of this in-between of algebra and analysis are of interest to you.

Take care
@qed