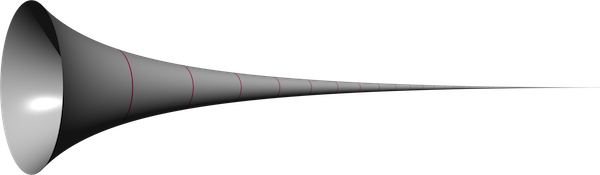
[Math Paradox #17] Covering Infinite Area using Finite Paint - Gabriel's Horn

mathsolver (53)in #math • 6 years ago (edited)

[1]

Paradox and Math

Be Careful!

Starting with this post, next 3 to 4 posts will be about paradoxes in Math. In fact, most of the topics that are considered as mathematical paradox are not real paradoxes anymore; there exist numerous solutions and logical reasonings for those problems. However, it is worth to discuss about them.

In this post, topic is about Gabriel's Horn, a mathematical object having finite volume but infinite surface area .

1. Torricelli's Discovery

In 1643, Evangelista Torricelli made his discovery of the strange nature of the acute hyperbolic solid, which we would now call the rectangular hyperboloid. It is generated by rotating the rectangular hyperbola

$y = \frac{1}{x} \ (x > 1)$

by $360^{\circ} (=2\pi )$ about the $x$ -axis.

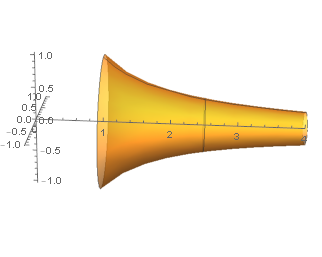
This is called Gabriel's Horn or sometimes Torricelli's trumpet. He showed that this infinite solid has a finite volume. To today’s post-calculus eyes this single fact is not shocking but it does become rather more surprising when we realize that not only is its length infinite, but so is its surface area. We will use calculus and modern-day notation to prove both results

the volume is finite and
the surface area is infinite.

2. Finite Volume

The volume of the solid formed by rotating the area between the curves of $y=f(x)$ , the lines $x = a$ , $x = b$ and the $x$ -axis is given by

$V =\pi \int_{a}^{b} f^2(x)dx$

Since Gabriel's Horn is infinite solid, we should take $b$ to infinity, $\infty$ . The calculation gives

$\begin{align*} V &= \lim_{b \rightarrow \infty} \pi \int_{1}^{b} \frac{1}{x^2}dx \\ &= \lim_{b \rightarrow \infty} \pi \left[ -\frac{1}{x} \right]_{1}^{b} \\ &= \lim_{b \rightarrow \infty} \pi \left(1 - \frac{1}{b} \right ) = \pi \end{align*}$

which is clearly finite.

3. Infinite Surface Area?!

The area of the solid formed by rotating the curve $y = f(x)$ along the $x$ -axis from $x=a$ to $b$ is given by

$A = 2\pi \int_{a}^{b} f(x) \sqrt{1 + (f'(x))^2} dx$

given that the function is continuously differentiable on interval $(a,b)$ . Luckily, out function $y = 1/x$ is continuously differentiable in $f'(x) = -1/x^2$ . Since

$\sqrt{1 + (f'(x))^2} = \sqrt{1 + \frac{1}{x^4}} > 1$

for all $x \in (1, \infty)$ , we have the inequality

$\begin{align*} 2\pi \int_{1}^{b} f(x)\sqrt{1+(f'(x))^2} &> 2\pi \int_{1}^{b} f(x) dx \\ &= 2\pi \int_{1}^{b} \frac{1}{x} dx \\ &= 2 \pi \ln b \end{align*}$

where $\ln$ denotes natural logarithm. Now taking the limit both sides give

$A \geq \lim_{b \rightarrow \infty} 2\pi \ln b = \infty$

so that the surface area of Gabriel's horn is infinite.

4. Painter's Paradox and Solution

So where is the paradox? Imagine the Gabriel's horn as a infinite cup. Then since volume is finite, we can fill the cup with finite amount, $\pi$ liter of paint. But at the same time, the paint would not be sufficient to coat its inner surface; as the surface area of a cup is infinite! This ironic situation is called the painter's paradox.

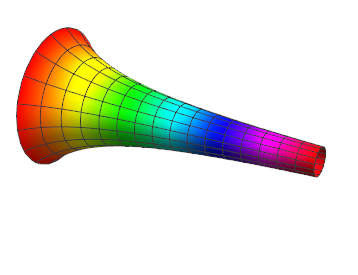
Is an infinite amount of paint really needed to paint the inner surface of the Gabriel's horn? Well, the answer is NO. The painter's paradox is resolved by realizing that a finite amount of paint can in fact coat an infinite surface area,

It simply needs to get thinner at a fast enough rate.

Painting a surface means applying a coat of paint on the surface. The thickness of coat, is NOT uniform all over the surface, it should become thinner as the horn goes to infinity. So what is exactly a fast enough rate? Remember the area formula

$A(t) = 2\pi \int_{1}^{t} f(x)\sqrt{1 + (f'(x))^2} dx$

for the surface of revolution defined on interval $x \in [1, t]$ ? By Fundamental Theorem of Calculus, the rate of change is equal to

$\begin{align*} \frac{dA}{dt} &= 2\pi f(t)\sqrt{1+(f'(t))^2}\\ & = \frac{2\pi}{t} \sqrt{1 + \frac{1}{t^4}} \\ &= 2\pi \frac{\sqrt{t^4 + 1}}{t^3} \\ &\sim \frac{2\pi}{t} \end{align*}$

Thus if we set the thickness of paint to be inversely proportional to the length of the throat of the horn, we can actually coat the surface with finite amount of paint! However, in real world, this is impossible; since the thickness of coating can not go infinitesimally small due to physical limitations.

5. What about the Converse?

[3]

Now a natural question arises.

Does there exist a surface of revolution that has a finite surface area but an infinite volume?

The answer is unfortunately NO...😕

Let $f(x)$ be continuously differentiable function on $[1, \infty)$ . Let $A, V$ be the surface area and volume of solid of revolution over $x$ -axis respectively. If the surface area $A$ is finite,

$\begin{align*} \lim_{t \rightarrow \infty} \left( \sup_{x \geq t} f^2(x) \right ) &= \limsup_{t \rightarrow \infty} \left( f^2(1) + \int_{1}^{t} (f^2(x))'dx \right)\ (\because \text{F.T.C}) \\ &\leq f^2(1) + \int_{1}^{\infty}|(f^2(x))'|dx \ (\because (f^2)' \leq |(f^2)'|) \\ &= f^2(1) + \int_1^{\infty} 2|f(x)||f'(x)| dx\ (\because (f^2)' = 2ff'))\\ &\leq f^2(1) + \int_1^{\infty} 2|f(x)| \sqrt{1 + (f'(x))^2} dx\ (\because |f'| = \sqrt{(f')^2} \leq \sqrt{1 + (f')^2}) \\ &= f^2(1) + \frac{A}{\pi} \end{align*}$

Therefore, we can deduce that

$M = \sup_{x \ge 1} |f(x)|$
is finite, using the fact that $f$ is continuous over $[1, \infty)$ . Now, the volume:

$\begin{align*} V &= \pi \int_{1}^{\infty} f^2(x)dx \\ &= \pi \int_{1}^{\infty} f(x)\cdot f(x)dx \\ &\leq M\pi \int_1^{\infty} f(x)dx \\ &= M\pi \int_1^{\infty} f(x) \cdot 1 dx \\ &\leq M\pi \int_1^{\infty} f(x) \sqrt{1 + (f'(x))^2} dx = \frac{MA}{2} \end{align*}$

should necessarily be finite!

Actually, the converse also does not holds for arbitrary rectifiable solids, because of isoperimetric inequality in 3D space but proving the generalized fact needs more mathematical concepts.

6. Conclusion

[4]
The painter's paradox, arises when our intuition of painting deviates from the mathematical concept of area. Also the concept of infinity should be treated rigorously, not just using simple simulations using real world applications (like painting) .

7. Citations

[1] Image Source Link

[3] Gabriel's Horn Explained Wiki Article

[4] On Painter’s Paradox: Contextual and Mathematical Approaches to Infinity (Article)

All other images are self-made using Mathematica.

#mathematics #science #steemstem #education

6 years ago in #math by mathsolver (53)

$0.25

Sort:

Trending

[-]

steemstem (73) 6 years ago

This post has been voted on by the steemstem curation team and voting trail.

There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!

$0.00

[-]

mathowl (64) 6 years ago (edited)

I remember this from my calculus course :D

The image [2] does not seem to have an online copy-right license attached to it. Please only use images for which there is a copy-right license for reuse. The link in the post has to link to the corresponding license. Correct usage of copy-right is a requirement for steemstem curation.