No solution! #1 - Prime numbers
Great to see you in the "No solution!" series! In mathematics, there are numerous open problems, i.e. problems where no correct proofs have yet been found. No matter you are good at maths or not, I hope you still enjoy my posts and will be astonished by the beauty of math! I will write in the simplest terms and will not include complicated mathematical arguments. If you like my posts, please upvote, resteem and follow me @manfredcml : )

(Picture source: https://pixabay.com/en/geometry-mathematics-cube-1044090/)
Mystery of prime numbers
Mathematicians always want to understand more about prime numbers. Let's have a quick review of what a prime number is. A prime number is a whole number greater than 1 which can only be divided by itself and one only. As a simple example, 5 is a prime number since we are left with a remainder if 5 is divided by any number other than itself or 1. The first few prime numbers are 2, 3, 5, 7, 11 and 13. You may come up with a question: are there infinitely many prime numbers? This is not an open problem and the answer is certain: YES. The proof of this claim is easy and you can quick find a proof on Google. One of those proof can be found here.
Well, there are infinitely many prime numbers, but how about its distribution? This will bring up a number of interesting conjectures about the distribution of prime numbers:
Twin prime conjecture
(5, 7), (11, 13), (17, 19) are all pairs of prime numbers whose difference between them is exactly 2. Any 2 prime numbers with exactly one number between them are known as twin primes. The famous twin prime conjecture is stated as follow:
Twin prime conjecture:
There are infinitely many prime numbers p such that p + 2 is also a prime number.
Unfortunately, this problem remains unsolved. Yet, the proof may not be far away. Top mathematicians, such as Australian mathematician Terence Tao, have been working on this problem and hopefully we may be able to see a correct proof in the coming 10 years.
Goldbach's conjecture
The statement of Goldbach's conjecture is easy to understand:
Goldbach's conjecture:
Every even integer greater than 2 can be expressed as the sum of two primes.
Let's try out several even numbers to see if the conjecture is correct for these simple cases. 4 can be expressed as 2 + 2, 20 can be expressed as 3 + 17 and 100 can be expressed as 3 + 97. Indeed, researchers have shown that this conjecture holds true for whole numbers up to 4,000,000,000,000,000,000! However, a proof for all even integers is yet to be discovered.
Riemann Hypothesis
This is perhaps the most remarkable unsolved problem that draws the attention of the top mathematicians in the world. Riemann Hypothesis is also one of the "Millennium Prize Problems". Any correct solution to a Millennium Prize Problem is awarded USD 1 million by the Clay Mathematics Institute. At present, only one of the seven Millennium Prize Problems has been solved.
Let us get back to the Riemann Hypothesis, which is about the distribution of prime numbers. It seems that the distribution of prime numbers does not follow any specific pattern. Yet, Riemann, a German mathematician, observed that the frequency of prime numbers is very closely related to the behavior of the so-called "Riemann Zeta function":
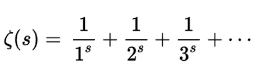
When s is a negative even integer, e.g. -2, -4, -6..., we can easily show that ζ(s) = 0. Such solutions are not interesting. The Riemann Hypothesis claims that all interesting solutions of the equation ζ(s) = 0 lie on a certain vertical straight line. Any correct solution to this hypothesis will be world-shocking!
Coming soon...
In the next post, let us explore another Millennium Prize problem --- the P vs NP problem.
References
Wikipedia - Twin Prime
Wikipedia - Goldbach's Conjecture
Millennium Problems - Riemann Hypothesis
I write articles on machine learning, applied statistics and economics to the best of my knowledge : ) If you like my posts, please upvote, resteem and follow me @manfredcml.
Other articles:
Be a smart gambler! #1 - Gambler's fallacy
Let's play a game #1 - Prisoner's Dilemma
Paradox is fun! #1 - Boy or Girl?
Prime number is definitely one of the most difficult topics that the world is yet to explore more about. The topic carries so much beauty in mathematics with it but is probably not interesting to many considering the proof may not be far from just a chunk of symbols to the laymen and its limited application in daily lives. But still, to people who have some mathematical background and are fond of it this is still a good thought provoking post! So don't be disappointed if only few value your post, I'd for one love to see more posts like this. Upvoted for support!
another great article about problems with no solutions! though I dun really understand your last part, what does the zeta function have to do with prime numbers?
Thanks for your support! For simplicity I don't explicitly show the details, but Riemann Zeta function can be expressed as a product of functions of all primes! Since the zeta function can be written in terms of primes, it follows that the roots of that function are somehow related to the distribution of primes. The magic of Riemann hypothesis is its simplicity but yet meaningful implications on primes.
Like so much mathematics, it is everywhere but it is hidden. Most people don't notice the algorithms, just the effects.
Prime numbers and modular functions are important in blockchain calculations.
nice information.