Find the Real Root of 4^x + 6^x = 9^x
Given a equation 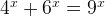 , let’s find the real value of x.
, let’s find the real value of x.
First, divide both sides by 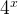 which becomes:
which becomes:
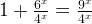
as 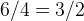 , and
, and 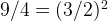 , it becomes:
, it becomes:
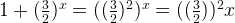
Let’s replace 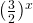 with
with  and further we have:
and further we have:
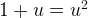 that is
that is 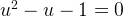
This equation has a golden root (the negative root should be discarded):
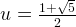
Therefore, 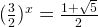
and 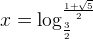
and 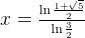
and we can compute the value x that is approximately 1.187.
--EOF (The Ultimate Computing & Technology Blog) --
Reposted to Blog
Every little helps! I hope this helps!
Steem On!~
If you like my work, please consider voting for me or Buy Me a Coffee, thanks!
https://steemit.com/~witnesses type in justyy and click VOTE

Alternatively, you could proxy to me if you are too lazy to vote!
Also: you can vote me at the tool I made: https://steemyy.com/witness-voting/?witness=justyy
I forgot mathematic 😂
;)
拍行长👏!shop
Hi~ justyy!

@yanhan has gifted you 1 SHOP!
Currently you have: 7 SHOP
View or Exchange
Are you bored? Play Rock,Paper,Scissors game with me!SHOPPlease go to steem-engine.com.