Math Trick: Finding the Square of a Number
Hi steemians, I would like to share my interest about one of the tricks in mathematics which is very helpful to the student.
Before I will start, let me share to you why I am posting this kind of article. A while ago, I was studying about math since I am going to take a board examination this coming September. So, I was searching on youtube about the tricks in mathematics which can be used for the upcoming board exam. During that time, there is a video which caught my attention so I click it.
Here is the video.
Honestly, I don't understand what he was talking about. I am just focus what he was writing on the board until I saw a pattern. In the end of the video, I feel frustrated because there is some questions in my mind which is not answered by the video like "what if we are going to find the square of the bigger number?" . So, I was searching the answer own my own. As the time pass, I see some pattern on how to find the square of the bigger number so I immediately get my pen and paper if that pattern works. Fortunately, it was working and I am so happy about my achievement. I wonder how did I get that pattern. I know, maybe this pattern that I am talking really exists but it's OK since I am the one who discover it own my own. So that's it. Now I am going to share to you the tricks.
Shortcut to find the square
11^2= 121
12^2= 144
13^2= 169
14^2= 196
15^2= 225
16^2= 256
17^2= 289
18^2= 324
19^2= 361
20^2= 400
21^2= 441
22^2= 484
23^2= 529
24^2= 576
25^2= 625
26^2= 676
27^2= 729
28^2= 784
29^2= 841
30^2= 900
Question.
Can we get the square of a number which is greater than 30?
Yes, we can get the square of the number if the number is less than or equal to 1,000 ( since if i am going to use the number greater than 1000, the tricks wont work so that's the limit that we can use our tricks). Before we will proceed in finding the square of a number, lets try some numbers above if it is really works.
For example. Find the square of 12.
Step 1. Square the last digit of the number.
Step 2. Square the 1st digit of the number.
Step 3. Multiply the 1st and the last digit of the number then multiply the product by 2.
Step 4. Get the sum of step 3.
Solution.

Therefore, 12^2 is 144. Indeed it is true.
Another example. Find the square of 25.
(Again, just follow the steps above.)

Therefore, 25^2 is 625.
In finding the square of a number which is greater than or equal to 100 but less than or equal to 1000, we cannot use the previous tricks instead we will try another tricks so that we can get the correct square of the number.
Example. Find the square of 100.
This tricks I am going to show you is only applicable to the number which is the 1st digit is an integer (1 until 9) and the rest of the number must be zeros. For example. 100, 200, 300, 1000, 20000, and etc.
Step 1. Count the numbers of zeros in the given.
Step 2. Double the numbers of zeros in the given. Example if the given is 700^2, then we can see that there are 2 zeros so, during this step the numbers of zeros will become 4.
Step 3. Get the square of the 1st digit.
Solution

Therefore, 100^2 = 10,000.
Another Example. Find the square of 102.
Step 1. Divide the number into 2 parts. One of them must be divisible by 100. (Note: In dividing a number in a two parts, make sure that if you are going to subtract the two numbers then the difference must be less than 100).
Step 2. Focus to the number which is not divisible by 100. The number that being focus must be multiply by 2 and then add the product of the number being multiplied and the number which is divisible by 100.
Step 3. Multiply the number that we get in Step 2 by the number of the first digit of the number which is divisible by 100. Example , the number that we get in step 2 is 270, then the first digit of the number which is divisible by 100 is 7, so we will multiply 270 to 7.
Step 4. Find the square of the number which is not divisible by 100.
Step 5. Find the sum.
Solution
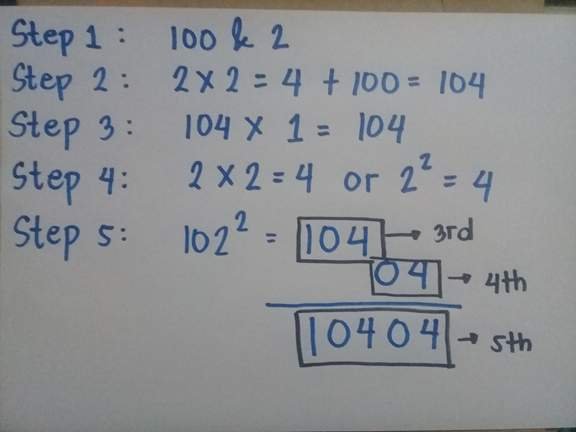
Therefore, 102^2 is 10,404. [check it by using calculator]
Another example. Find the square of 736.
(Just follow the steps above)

Therefore, 736^2= 541,696
Last Example. Find the square of 999.

Therefore, 999^2 is 998,001.
I think that's all I can share to you. I hope that this post will help you to cope up the difficulty of mathematics. Thank you for reading and Good Evening. Please feel free to comment. :D
Wow! That is so awesome :) this helped a lot.
Though I have memorized the squares from 1 - 30.
Thanks.. hehehe
wowwww!, karon pa ko . Noted @jhernel45 :)
haha, nag experiment ra man ko ana van, pero nakuha raman nako. pero nosebleed ko sa video wa koy nasabtan. hahaha
Pun i pa imong tags nel haha make it 5 para nice :D
hahaha cge2 maghuna2 sa ko :D
naninga jhernel ah 😂😂
hahaha panagsa rana.
Congratulations @jhernel45! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBookmarked this one hehe.. Soon it help....
Ohh thanks. I appreciate your support.
https://steemit.com/math/@jhernel45/math-finding-gcf-greatest-common-factor-using-the-euclidean-algorithm
You can have this one. I am sure, it will really help you. :D