Monty Hall Problem
You are on a gameshow and have a choice between three doors (door A, B, & C), and behind two of the doors is nothing and behind the third door is a great prize, and the hosts asks you to pick one.
Before the host shows you what is behind your door, he chooses one of the two that he knows is empty and shows you the results.
Now, he smiles back at you with that gameshow grin and asks you if you want to stick with your door.
What do you do?
The answer is simple- you 100% of the time....
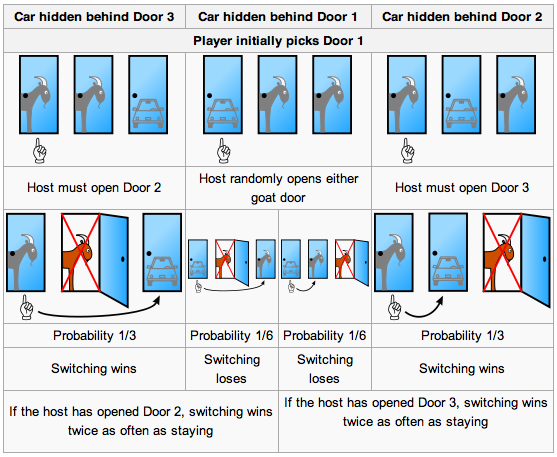
ALWAYS change your choice!
A lot of people think that once they eliminate the one door that now you are down to 50/50 which is incorrect.
When you first started the game you only had a 1 in 3 chance of being correct, which is still the same if the host removes one of the two doors. When you originally picked and he removed a door does not lower your chances of being incorrect- your chance remains at 1/3.
If you change doors - you have a 2/3 chance of being correct!
If you played the game 600 times and you stuck with your original choice every time, you would expect to be right 200 times (yeah!), however that means you would be wrong 400 times (boo!).
The game show host will always remove one of the incorrect doors, so if you always switch doors- you can safely say that you will be right 400 times (double hooray!) and incorrect 200 times (1/2 boo!).
Don't you just love math! :)
Congratulations @foodie4lf! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honnor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBy upvoting this notification, you can help all Steemit users. Learn how here!