Vieta's Formulas
Francois Viete, for whom the topic of this post is named. Source: Wikipedia.org, Public Domain
François Viète was a French mathematician who worked in the 16th century, and one of the earliest to combine classical Hellenistic techniques with the then-novel techniques of Algebra introduced from the Arab world. He worked as a lawyer and as an adviser to Kings Henry III and Henry IV of France [1], nut is perhaps best known today for the set of formulæ that bear his name, called "Vieta's Formulæ". Vieta's formulæ are a set of rules that relate the coefficients of a polynomial to the roots.
The Quadratic and Cubic Cases
Let us consider the function
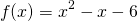. It is clear, even to younger students, that this expression can be factored to 
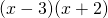, yielding the roots 
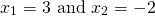. Multiplying the two roots gives us 
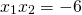and adding them gives us 
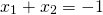. These are the same as the coefficients of the quadratic function (-1 and -6). This should not be very surprising given that, by the FOIL method, we might write 
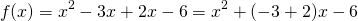. In fact, it can easily be shown, using the quadratic formula that, for 
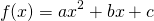, if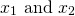 
are solutions, then: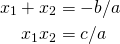
The proof of the above involves only elementary algebra, and will be left to the reader.
If we consider a cubic case such that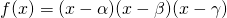 
, it's obvious that the zeroes of this function are 
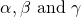. If we re-write the function by expanding it, we obtain:
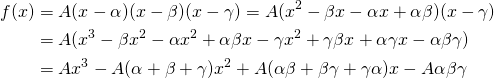
And equating coefficients so that
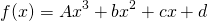, we can write the following:
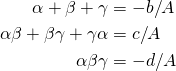
Vieta's Formula for Higher Powers
Now, our goal should be to extrapolate the patterns for higher powers. We might guess, based on the pattern that the coefficients can be deduced by multiplying and adding the zeroes. To do this, we first introduce the elementary symmetric sum:
The k-th elementary symmetric sum of a set of n elements is the sum of all products of k elements - without repeating an element - from that set.
For example in the cubic case,
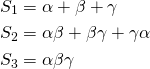
And in the quartic case:
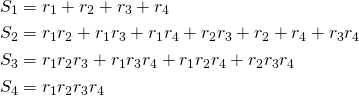
It is now easy to see, by induction that, for a polynomial of degree n: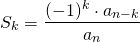 
, where 
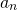is the leading coefficient.
Sources:
I'd listen to kryzsec, he's trying to help. Also from experience people aren't to fond of equations. Take a look at some of the trending articles on steemstem and see how they are. These are quite complex and only a handful of people are going to have any idea of what they mean of the significance. I hope that helps.
Thanks. I'll try and cut down on the formulas and use more graphics in the future. Although part of the reason for blogging is so that I can have stuff to share with my students in real life, and this just happens to be something we talked about today.
I have to disagree. Popularization is not the object of creation, but meaningfulness and in depth research is.
If you have experience of writing on here for a certain audience then you'll understand. If no one understand the maths then they become lost in the subject you're trying to teach them. Here we are not in school but writing blogs....
It would be cool to see another reference or 2 on this.
Most of the equations here have been in the public domain for hundreds of years, seeing as Viete died in the 1600's. Though I've added a few references, as well as Viete's original work.
I didn't think you stole them, I thought it would make it better if people that we interested had further reading to watch
Yeah, I just wanted to clarify (in the interest) that I didn't steal them. I just thought they were interesting, because despite these formulas being hundreds of years old, they aren't really found in modern textbooks (It's not exactly cutting edge stuff here). As you might have deduced from my other posts, I'm quite fond of historical mathematics and Viete was one of the earliest to bridge the gap between ancient and modern methods mathematics.
Also, how did I get 93 votes? I went to get a glass of water and suddenly I'm getting a lot of votes.
Every time I see the work of an ancient mathematician I feel amazed because they did all those discoveries without any calculator whatsoever!
I think it shows what the human mind is capable of. Euclid wrote much of the Elements employing only a compass and a straightedge. And also if you consider that in ancient times, many mathematicians also combined their studies of mathematics with other professions or studies such as philosophy (Decartes), law (Viete), or poetry (Khayyam), it's truly amazing how they were able to do so much at a time when even books were hard to come by.
Good job with the typesetting; the article is well organized.
Also good to see you linked to the original book.
I remember playing around with these equations in undergrad more than 20 years ago!. :)
The insight of the original algebraists is astounding. They came up with so many elegant tricks.