Finding the height of a Sea Island: A 1800-year old math problem
In a previous post, I wrote about how ancient surveyors attempted to find the height of a sea island. Keeping in mind, this was largely before the advent of trigonometric tables, the methods they developed were purely Euclidian in nature, relying on principles of similarity, and using algebraic geometric techniques. In this post, I will present the solution to the Sea Island problem using Liu Hui's method.
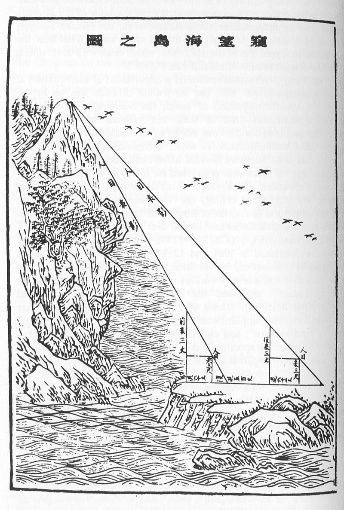
A plate from an 18th century reproduction of the Haidao Suanjing
wikipedia; Open Domain
Liu Hui's Difference Theorem
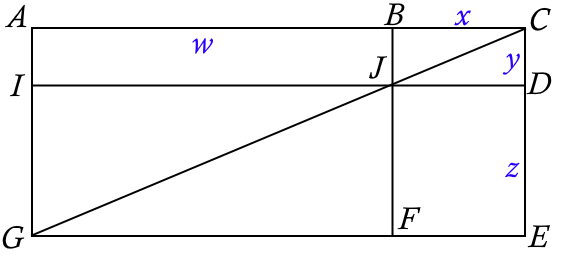
In modern language, the theorem might be stated:
Consider rectangle ACEG having diagonal GC. AC and CE are divided by perpendicular lines BF and DI respectively, such that the intersection of BF and DI, J lies on the diagonal. In this case, the areas of rectangles ABJI and JDEF are equal.
Proof
Triangles ACG and GCE are congruent due to GC being the diagonal of the rectangle. GIJF and BCDJ are also rectangles, and since they also share the diagonal GC, triangles BJC and CDJ are congruent to each other, and triangles IJG and FGJ are also congruent to each other. Therefore the sum of the area of BJC and IJG is equal to the sum of the area of CDJ and FGJ. Subtracting these from ACG and GCE shows that ABJI and JDEF have the same area.
The Height of the Sea Island
Liu Hui's method essentially repeats the above theorem several times in order to find the answer algebraically.
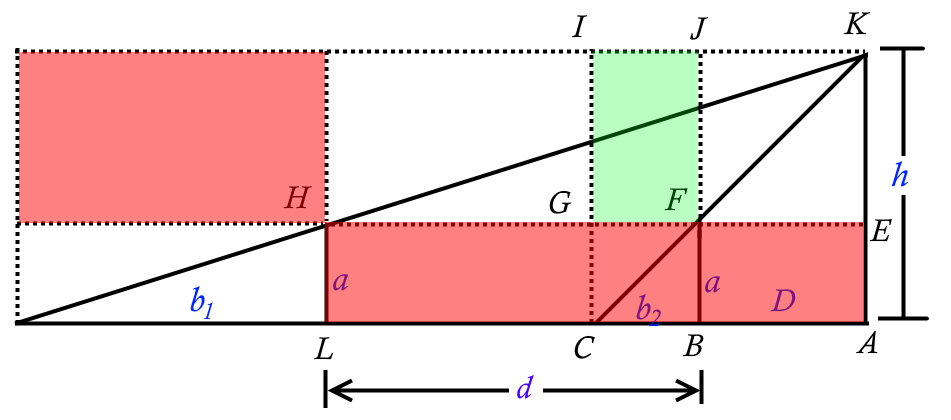
First we re-draw our diagram such as to include a "scaffolding" around the relevant points, and observe the following
- Clearly, a(d+D) = b1(h-a) (shown in red)
- Also, aD = (h-a)b2 (shown in green)
- Therefore, ad + aD = b1(h-a) and
- Rearranging and substituting ad = b1(h-a) - (h-a)b2
- Factoring the above gives: ad = (h-a)(b1-b2)
- Therefore:
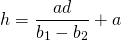
Moving onto the distance:
- We observe that Da = b2(h-a). Having already calculated h we can calculate the value numerically.
Putting the measurements from the given problem, we obtain:
a = 30 feet
d = 6000 feet
b2 = 738 feet
b1 = 762 feet
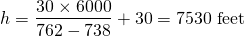
Converting these, we obtain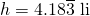 
, or 4 li and 55 paces.
Similarly, placing this number into the equation for the distance to the island gives 102 li and 150 paces.