DETERMINANTE DE UN ENDOMORFISMO

DETERMINANTE DE UN ENDOMORFISMO
1. DETERMINANTE DE UN ENDOMORFISMO
Sea ϴ:F→F un endomorfismo, donde F es un módulo sobre R, libre y de rango n. Se sabe que la potencia exterior ΛnF es un módulo sobre R, libre y de rango
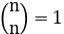 y por lo tanto ΛnF≅R. Aquí se supondrá siempre que R es un anillo conmutativo con identidad.
y por lo tanto ΛnF≅R. Aquí se supondrá siempre que R es un anillo conmutativo con identidad.Sea Λnϴ: ΛnF →ΛnF, veamos que es una homotecia que no depende la base elegida de ΛnF . En efecto, sen x, x´ dos bases de ΛnF, luego x´=βx. Si Λnϴ(x)= αx, entonces Λnϴ(x´)=βΛnϴ(x)=β( αx)= α(βx)=αx´.
Se define det( ϴ)=α.
Dada una base e1,...,en de F, luego ϴ(ei)=∑ j=1naijej, luego
Λnϴ(e1Λ...Λen)=(∑ σ∈Ssigσ(a1σ(1)...anσ(n)))e1Λ...Λen. Es decir
det( ϴ)=∑ σ∈Snsigσ(a1σ(1)...anσ(n)), fórmula bastante conocida.
2. PROPIEDADES DE LOS DETERMINANTES
Teorema 2.1(Desarrollo del determinante por los elementos de una columna) Si A=(aij)∈Mn×n(R) y
Ars=det(1,...,r^,...,n:1,...,s^,...,n)=[ 1,...,r^,...,n:1,...,s^,...,n]), entonces
det(A)=∑ r=1n(−1)r+sars[ 1,...,r^,...,n:1,...,s^,...,n].
Aquí (1,...,r^,...,n:1,...,s^,...,n) es la matriz que se obtiene de la original, sustrayendo la fila r y la columna s, respectivamente y [ 1,...,r^,...,n:1,...,s^,...,n]=det (1,...,r^,...,n:1,...,s^,...,n) .
Demostración . Sea e1,...,en una base de F. Podemos definir
ϴ(ej)=∑ i=1naijei (j=1,2,...,n).
Se sabe que Λnϴ(e1Λ...Λen)=det(aij).
Es claro que Λnϴ(e1Λ...Λen)=(−1)s-1ϴ(es)Λϴ(e1)Λ...Λϴ(es)^Λ...Λϴ(en)
Se sabe que ϴ(es)=∑ i=1naisei (i=1,2,...,n), por lo tanto
ϴ(e1)Λ...Λϴ(es)Λ...Λϴ(en)=
(−1)s−1(∑ i=1naisei )Λϴ(e1)Λ...Λϴ(es)^Λ...Λϴ(en)=
(−1)s−1∑ i=1naisei Λϴ(e1)Λ...Λϴ(es)^Λ...Λϴ(en).
Lo anterior aseguro, que cuando i se fija, podemos sustraer aijei en cada ϴ(ej).
Sea L´un módulo sobre R de rango n−1 con base e1´,...,en−1´. Se define ϴr: L´→F mediante ϴr(ei´)=ei (1≤i<r) y ϴr(ei´)=ei+1 (r ≤i).
Sea ϴs:F→L´por ϴs(ei)=ei´(i<s), ϴs(es)=0 y ϴs(ei)=ei−1´ (s<i).
Sea hrs=ϴs∘ϴ∘fr. Se prueba que det( hrs)=Ars=[ 1,...,r^,...,n:1,...,s^,...,n].
Estudiemos la expresión ϴ(e1)Λ...Λϴ(es)^Λ...Λϴ(en)
Se ha supuesto que ϴ(ej)=∑ t≠iatjet (j≠s) y se puede identificar con un operador his, por lo tanto
eiΛϴ(e1)Λ...Λϴ(es)^Λ...Λϴ(en)=AiseiΛe1Λ...Λei^Λ...Λen.
Se concluye que
(−1)s−1∑ i=1naisei Λϴ(e1)Λ...Λϴ(es)^ Λ...Λϴ(en)=
(−1)s−1∑ i=1naisAiseiΛe1Λ...Λei^Λ...Λen
=
( ∑ i=1n (−1)s−1+i+1aisAis)e1Λ...Λen.
Es decir det(A)=∑ i=1n (−1)s+iaisAis∎
3. DESARROLLO DE LAPLACE DE UNA MATRIZ
Proposición 3.1. Si A=(aij)∈Mn×n(R), entonces
∑ i=1nair[ 1,...,i^,...,n:1,...,s^,...,n]=det(A)δrs
Demostración. Sea B=(bij) ∈Mn×n(R), tal que bir=bis=air (i=1,2,..,n) con s≠r, y bij=aij el resto de los casos. Tenemos que
∑ i=1n(−1)i+sais[ 1,...,i^,...,n:1,...,s^,...,n]=0
entonces
(−1)s∑ i=1n(−1)iais[ 1,...,i^,...,n:1,...,s^,...,n]=0
Se deduce que
∑ i=1n(−1)iais[ 1,...,i^,...,n:1,...,s^,...,n]=det(A)δrs.
∎4.RESOLUCIONES DE ECUACIONES LINEALES HOMOGÉNEAS
Recordemos que si A=(aij)∈Mm×n(R), y t≤min(m, n), podemos considerar It(A) el ideal generado por todos los determinantes de submatrices de de A de tamaño t×t. Es claro que It(A) ⊆ Is(A) si s≤t. Recordemos que Ann(It(A))={a∈R: a.α=0, para todo α∈It(A)}.
Definición 4.1 Sea A=(aij)∈Mm×n(R) y r≤min(m, n). Se dice que r=rk(A) es el rango de la matriz A, si r=max{t: Ann(It(A))=0}.
Teorema 4.1 (McCoy). Sea el sistema de ecuaciones lineales homogéneas:
a11x1+...+a1nxn=0
........................
am1x1+...+amnxn=0
El sistema de ecuaciones lineales homogéneas tiene solución no trivial, si y sólo si, la matriz A tiene rango menor que n.
Demostración. Para ver el directo, es claro que el resultado vale si m
<n, ya que r=rk(A)≤min(m,n)=m <n. Sea B= (bij)∈ M n×n (R) una submatriz de A de tamaño n×n y B^=(bij^)=cofji(B) donde bij^=(−1)i+j[ 1,...,j^,...,n:1,...,i^,...,n]. Se sabe que B^B=det(B)In×n. De esta última expresión deducimos que xidet(B)=0 para todo i=1,2,...,n y como un xi≠0, se deduce el directo.
Para ver el recíproco, sea r=rk(A), luego existe a≠0 tal que a∈ Ann(Ir+1(A)). Si r=0, entonces a∈ Ann(I1(A)). Es claro que (a,a,...,a) ∈Rn es solución del sistema. Supondremos por lo tanto 1≤r <min(m.n), luego existe un menor [ i1,...,ir:j1,...,jr], tal que a.[ i1,...,ir:j1,...,jr]≠0. Sin pérdida de generalidad, supondremos que este menor es:
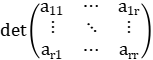 =[ 1,...,r:1,...,r].
=[ 1,...,r:1,...,r].
Sea ci=cofr+1,i=(−1)i+r+1[ 1,...,i^,...,r+1:1,..,r] (i=1,2,...,r+1) y consideremos los escalares xi=cia, luego xr+1=[ 1,...,r:1,...,r]a≠0. Probemos que (x1,...,xr+1,0...,0) es una solución no trivial del sistema de ecuaciones lineales homogéneas. Veamos que
ai1x1+...+ai(r+1)xr+1=0 (i=1,2,...,m).
En efecto si 1≤i≤r, entonces
ai1x1+...+ai(r+1)xr+1=
a(∑ j=1r+1aij(−1)j+r+1[ 1,...,j^,...,r+1:1,..,r+1])=
a(−1)r+1(∑ j=1r+1aij(−1)j[ 1,...,j^,...,r+1:1,..,r+1]=
a(−1)r+1δi(r+1)=0.
Supongamos ahora que i≥r+1 y consideremos la matriz
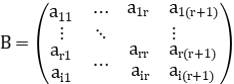 =
=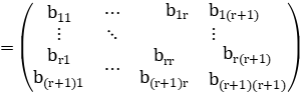
luego det(B)=∑ j=1r+1(−1)j+r+1b(r+1)j[ 1,...,j^,...,r+1:1,...,r,(r+1)^]=
∑ j=1r+1(−1)j+r+1aij[ 1,...,j^,...,r+1:1,...,r,(r+1)^]. entonces adet(B)=0 ya que B es un menor de orden r+1 y por lo tanto
ai1x1+...+ai(r+1)xr+1=0 para i≥r+1 . Se termina la prueba.∎
Corolario 4.1. Sea f:F→G endomorfismo de R-módulos libres de rangos n y m respectivamente. Dadas las bases {e1,...,en} y {é1,...,ém} de F y G respectivamente; entonces f es inyectiva, si y sólo si, el rango de la matriz A=(aij)∈Mm×n(R) es n, donde f(ej)=∑ i=1maijéi.
Demostración. Para ver el directo, supongamos que f:F→G es inyectivo. Si rk(A) <n . luego ∑ i=1naijxi=0 tiene solución no trivial , luego ∑ j=1nxjej≠0 y como f(∑ j=1nxjej)=0, llegamos a una contradicción. El recíproco se sigue fácilmente.∎
Ejemplo 4.1. Dado el sistema de ecuaciones lineales homogéneos con coeficientes en Z3
x−2y−z−w=0
y−w=0
x−y+z=0
Halle una solución no trivial usando el método de McCoy.
Solución.
Sea la matriz
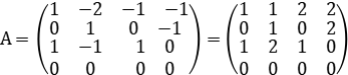
Es directo ver que rk(A)=r=3 y a=1∈Ann(I4(A))
Sea el menor

Luego
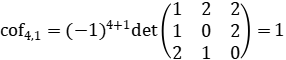
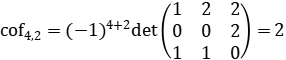
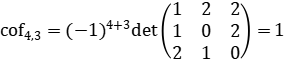
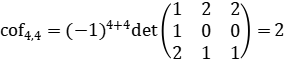
Entonces (acof4,1,acof4,2,acof4,3,acof4,4)=(1,2,1,2) como es inmediato verificar.∎
5. DUAL DE UNA POTENCIA EXTERIOR
Teorema 5.1 Sea M un módulo libre sobre R y de rango n, entonces para todo r≥0 se tiene que (Λr(M))*≅Λr(M*).
Demostración. Si r=0, el resultado se sigue. Sea r >0. Dadas las funcionales f1,...,fr, se define d:Mr→R por d(x1,...,xr)=det(fi(xj)). Es fácil ver que d es multilineal alternada. Existe por lo tanto η:Λr→R tal que η(x1Λ...Λxr)=det(fi(xj)). Se define ζ:(M*)r→ (Λr(M))* por ζ(f1,...,fr)= η. Se prueba que η es multilineal alternada. Existe por lo tanto ϴ:Λr(M*)→(Λr(M))* tal que ϴ(f1Λ...Λfr)=ζ(f1,...,fr)= η.
Para concluir la prueba consideremos una base {e1,...,en} de M y su base dual {e1*,...,en*} .
Definamos Ψ:(Λr(M))*→Λr(M*) por Ψ(g)=∑ 1≤i1<...<ir≤n xi1....ir ei1*Λ...Λeir* donde xi1...ir=g(ei1Λ...Λeir).
Consideremos la composición ϴ∘Ψ(g)=∑ 1≤i1<...<ir≤n xi1....ir ϴ(ei1*Λ...Λeir*), luego ϴ∘Ψ(g)(ej1Λ...Λejr)=∑ 1≤i1<...<ir≤n xi1....jr ϴ(ei1*Λ...Λeir*)(ej1Λ...Λejr)=∑ 1≤i1<...<ir≤n xi1....irdet(eis*(ejt)=xj1....jr., de lo que se deduce la inyectividad. Realmente es también sobreyectiva. Note que {ϴ(ei1*Λ...Λeir*) } es la base dual de {ei1Λ...Λeir }. Se prueba lo pedido.∎
REFERENCIAS
(1) William Brown: Matrices over conmutative rings. Marcel Dekker. New York. 1993.
(2) A. Micali y O. Villamayor: Estructuras algebraicas IV (Agebra multilineal) O.E.A. Washinton D.C. 1976.
🎉 ¡Felicitaciones! 😊 Por leer este contenido interactivo y educativo sobre álgebra multilineal 📚 ¡Esperamos que hayas disfrutado de la experiencia de aprender algo nuevo en un ambiente divertido y atractivo! 💡 ¿Tienes alguna pregunta o comentario? ✍️ ¡No dudes en compartir tus pensamientos y preguntas en los comentarios! 🤔
👉 Vota por nuestro testigo 'xpilar.witness' 👉 (https://steemitwallet.com/~witnesses) para ayudarnos a continuar contribuyendo al crecimiento y éxito de la comunidad Steem. ¡Gracias por tu apoyo! 💕