BREVES MATEMÁTICOS (PUNTOS DE MEJOR APROXIMACIÓN)

En el espacio cartesiano R²={ x, y : x, y ∈ R } hay dos tipos notable de normas, a saber:
||(x, y)||₁ = max { |x|, |y| } (norma del máximo)
||(x, y)|||₂ = (|x|²+ |y|²)^1/2(norma euclidea)

Ellas definen por lo tanto dos tipos de métricas:

d₁((x, y), (x´, y´)) = ||(x´ − x, y´ − y)||₁

d₂((x, y), (x´, y´)) = ||(x´ − x, y´ − y)||₂

Observemos dos tipos de comportamientos de estás métricas. Primero definamos un concepto importante en la geometría de los espacios vectoriales normados (X,||. ||):

---

Dado un subespacio lineal M y un punto w ∉ M, diremos que z ∈ M es un punto de mejor aproximación para w, si

||z − w|| = inf _m∈M ||m − w||= δ(w, M)= δ.

---

El punto de mejor aproximación podría o no existir, y en caso de existir podría no ser único. Consideremos tres ejemplos:

---

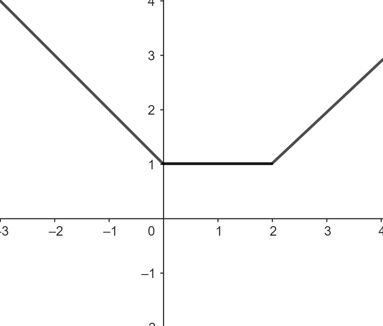
(a) Sea (R², ||(x, y)||₂) y M = { (x, y): y = 0 }. Dado el punto w=(1,1), tenemos que

inf_z∈M|m − w||₁= inf { ||(x − 1, − 1)||₁: x ∈ R} =inf { max(|x − 1|, 1): x ∈ R}

Es claro que max(|x − 1|, 1)=1, para 0 ≤ x ≤ 2; mientras que max(|x −1|, 1) > 1 para |x − 1| > 1. Es decir cualquier punto m = (x, 0) con 0 ≤ x ≤ 2 es un punto de mejor aproximación para w = (1,1). La gráfica de la función continua f(x, 0) = max(|x − 1|, 1) para todo (x, 0) ∈ M da una idea geométrica donde están los puntos de mejor aproximación:

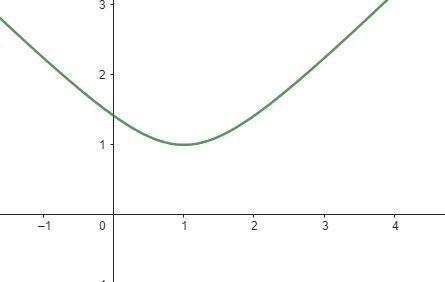
(b) Sea (R², ||(x, y)||₂) y M = { (x, y): y = 0 }. Dado el punto w = (1,1) , tenemos que

inf_z∈M||m − w||₂ = inf {||(x − 1, − 1)||₂: x ∈ R} =

inf {((x − 1)² + 1)^1/2: x ∈ R } = ||(1,0) − (1,1)||₂ = 1

donde el punto m =(1,0) de mejor aproximación para w = (1,1) es único. La gráfica de la función continua f(x, 0) =((x − 1)² + 1)^1/2 para todo (x, 0) ∈ M da una idea geométrica donde está el punto de mejor aproximación:

(c) Sea X = C[ 0, 1] el espacio vectorial de las funciones continuas a valores reales definidas sobre el intervalo cerrado [ 0, 1]. Aquí se considera la norma ||f|| = sup_{t∈ [0, 1]}|f(t) |. Sea M = P[ 0, 1] las funciones polinomiales reales de cualquier grado definidas sobre [0, 1] . Si w =f(t)=¹/_(1-t) para todo t ∈ [ 0, 1] y p_n(t) = 1 + t² + ⋯ + tⁿ ∈ P[ 0, 1] , tenemos que

||p_n(t) − f|| = sup_{t∈ [ 0, 1]} | 1 + t² + ⋯ + tⁿ−1/(1−t) | =

sup_{t∈ [0,1]} tⁿ⁺¹/(1-t)→ 0 cuando n →+ ∞.

Se deduce que δ(w, M) = 0 y es fácil demostrar que ninguna función polinomial p_n(t) es una mejor aproximación para f(t) =1/(1−t).


Lo anterior sugiere preguntarse en qué tipo de espacios vectoriales normados, la mejor aproximación se alcanza en un sólo punto.


Diremos que un espacio vectorial normado es estrictamente convexo, si dados dos vectores unitarios distintos v, z ∈ X, se tiene que ||v + z|| < 2.



Pasemos ahora a demostrar que si X es un espacio normado estrictamente
convexo, M un de subespacio lineal de X y w ∉ M, si en dos puntos z₁ , z₂ ∈ M se alcanza la mejor aproximación a w, entonces z₁ = z₂ .


En efecto, si ||z₁ − w|| = ||z₂ − w|| = δ, entonces ||( z₁ −w)/ δ||=||( z₂ −w)/ δ||=1, luego por simplificación, llegamos a que ||(z₁ +z₂ )/2− w|| < δ, y como (z₁ +z₂ )/2 ∈ M, llegamos a que z₁=z₂ , en caso contrario obtenemos una contradicción.