Machine learning "from scratch" #1 About artificial neurons - perceptrons
What is and how does artificial neuron work? How does signal pathway look? Why do we need activation function? What is perceptron? How man who invented ECG for heart diseases detection did help engineering of machine learning?
Let’s turn back in history
Until 1906 people used to think that human brain is "pure-solid" mass, because they did not know its construction. Of course they knew that brain takes a part in every process of human life, but they could not explain how it works. Everything has changed when Santiago Ramón y Cajal showed structure of the brain, and shape of single neuron by using simple photographic technique. That was a revolution.
People had to change their way of thinking, that was the condition for next discoveries. I am sure that you heard about Willem Einthoven - a man who invented ECG electrocardiogram using in heart diseases detection. He conducted research on biopotentials of organs tissues, including neurons and thanks to him mathematicians wanted to explore this topic and “translate” biological process to numeric model. That is why in 1943 Warren S. McCulloch and Walter Pitts has explained in mathematical way how single neuron works. Their theorem was used by Frank Rosenblat and Charles Wightman to build from relays first artificial neural net - perceptron - which was trained on character recognition.

And that is how our journey begins.
Journey - start
Perceptron is a net built from single or many artificial neurons, which are placed in the layers. In fact, it is an algorithm - some kind of mathematical function which takes some arguments (inputs) and return one response (output). Single neuron is a binary classificator what means that after training it can response for given problem (classify to two possible groups) by using answers “yes, I recognize it” or “no, I do not recognize it” or more much simple as “true” or “false”, or just by using numbers “1” or “0”. That is why we call it “binary”, because it response could be only bivalent. If we take a look for how humans perception works, we will see that everything comes down to Boolean algebra - We also classify that for example “something is warm”, or “something is not warm”, “there is a wall next to me”, or “there is no wall next to me” - true or false. Of course human brain is much more complex than every artificial neural net built nowadays and we classify things in a more extensive way, e.g. something is warm, much more warm or super-warm but science had found the way to solve that problem, so-called fuzzy logic - where numbers can be a real values between 0 to 1 (Btw. fuzzy logic had been studied, as infinite-valued logic notably by Jan Łukasiewicz and Alfred Tarski - my compatriots from Poland).

But what's the matter..?
Let’s consider construction of the biological neuron by Mr. McCulloch's and Mr. Pitts’s method. We will make some analogy and construct mathematical model which could be usable in engineering.
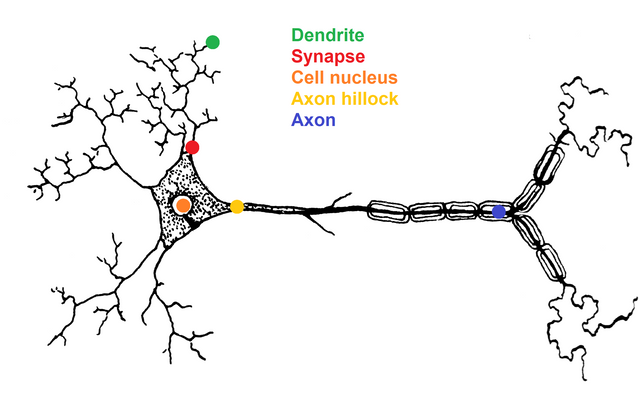
Neurons are made of:
- dendrites - where impulses are given (e.g. electrical impulses like in 60s, or if we talk about programming - number values). Dendrites are called “inputs” of neuron.
- synapses - they are some kind of gates and amplifiers of signals which flows through them. Synapses have some weight (number value) by which input impulses will be multiplied. Every dendrite has his own synapse.
- cell nucleus - it summing up all of amplified signals
- axon hillock - it works as activation function, which describes what will be given to output (without activation function neuron is like unscrewed but not squeezed tube of toothpaste - remember that we’re going to brush our teeth and we need that toothpaste)
- axon - output, where response will be given
Now we’re going to create block scheme.
Let’s also make a gentleman’s deal that we accept this dictionary below for future description:
dendrite - input x
synapse - weight w
cell nucleus - sum block
axon hillock - activation block
axon - output y
signal - some number value, a variable s
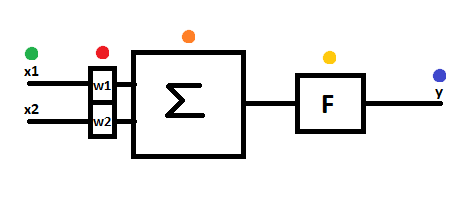
Of course number of inputs could be infinite - biological neuron has thousands of dendrites - but for simpler analysis of signals flow let’s consider two-input neuron.
- We are giving the input signals
x1andx2 - Signal
x1is multiplying by weightw1of its synapse, and signalx2is multiplying by weightw2of its synapse. We are getting equation: - To summing block are flowing signals
s1 = x1w1ands2 = x2w2, which are summing up. We are getting equation: - Summed signal is flowing to activation block, where activation function will classify it, and set output
y.
s1 = x1w1
s1 = x1w1s2 = x2w2
s2 = x2w2SIGNAL_SUM = s1 + s2 = x1w1 + x2w2
SIGNAL_SUM = s1 + s2 = x1w1 + x2w2
In more formal mathematics for case with infinite number of inputs:
SIGNAL_SUM = Σi = 0 xiwi
SIGNAL_SUM = Σi = 0 xiwi
where:
i - input number
y = ACTIVATION(SIGNAL_SUM)
y = ACTIVATION(SIGNAL_SUM)Now we know signal pathway and what happens during this signal flows (simple mathematic). Let's tell something more about activation function. In theorem, it could be every function we want - we need it for normalize response given to output - but in practic better if it is a non-linear function. For single neruon there is no difference, but for neural net asymmetry is important. The simplest but still usable activation function could be unipolar step function. Let's consider it.
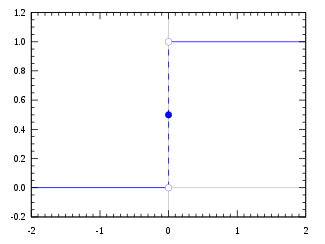
- if SIGNALS_SUM is higher than 0 then set output as 1 (true) | y = 1 SIGNAL_SUM > T = 0
- if SIGNALS_SUM is lower than 0 then set output as 0 (false) | y = 0 SIGNAL_SUM < T = 0
where:
T - is activation threshold, in this case we set threshold as 0
There is a possibility that our neuron could classify with satisfying accuracy, but does single neuron could solve every problem? Unfortunately not - well, nobody is perfect.

Single neuron is able to classify only linearly separable data sets (in graphic representation that are these data sets which we can separate by straight line). Case with two inputs could be shown in Cartesian coordinates.
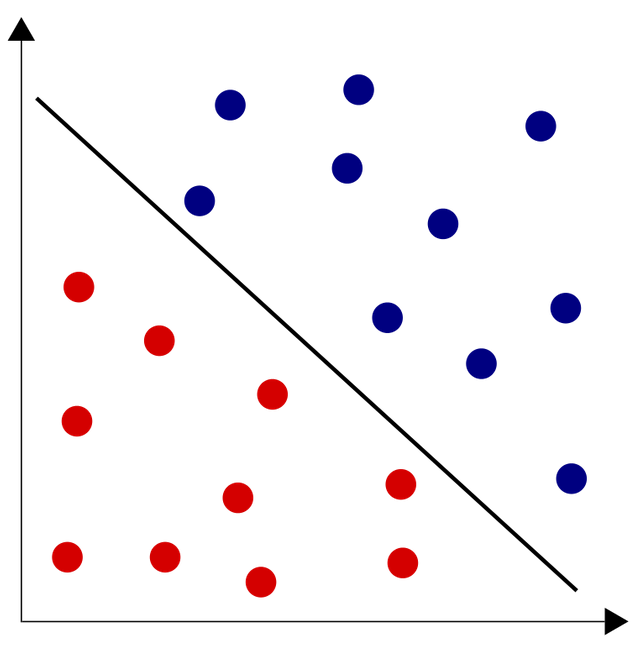
Fortunately we can combine single neurons into complex networks, creating many layers of them. That give us a really powerful tool which can classify even linearly non-separable data sets and solving multiclass problems e.g. dynamic perception of autonomous vehicles.

Summary
In my opinion neural networks are really interesting field of science (and art), which makes forward technology world. That is the way of the future.
Btw. I'm going to write series about machine learning in my native language, but I would like to translate more of my articles to english. Please, let me know if there are any people interested in neural networks who would read more about them "from scratch".

Thanks for your attention!
Bibliography
- R. Tadeusiewicz "Sieci neuronowe" Akademicka Oficyna Wydaw. RM, Warszawa 1993. Seria: Problemy Współczesnej Nauki i Techniki. Informatyka.
Next time use #steemstem tag - I think that this article is worth it :)
Też myślę, że warto. Tylko, że #steemstem wymaga podania dokładnego źródła wszystkich grafik i muszą one być w domenie publicznej i nie może być co do tego żadnych wątpliwości. To jeden z warunków otrzymania od nich nagrody.
Dziękuję Panowie :) Co do źródeł grafik - wszystko dopracuję!