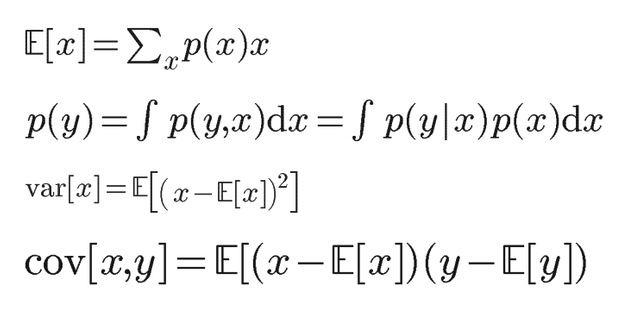Machine Learning

In order to learn something, you have to make a series of assumptions about the problem at hand. We make decision based on a set of beliefs and machine learning (ML) tries to place a quantative framework on this so that we can apply it to practical, real world issues. The maths was developed a fair amount of time ago but only recently has the computing power and data storage capability been made available to really exploit it and solve import problems. 

Probability

We are trying to learn things in an uncertain world. It is natural that we should work in the probabilistic regime. Lets introduce some basic concepts:

• Random Variables: These are the outcomes of a random process/event and encodes the degree to which we expect the outcome to be true. 
• Bayesian Probability: Traditionally, we view probabilities as the frequency of something happening. but in ML, we take the Bayesian viewpoint of probability which also quantifies the uncertainty in our assumptions. This is an important non-trivial point. 
• Models: A model is a conditional distribution that relates events/phenomena. 
• Probability Mass/Density Function: A function defined over an outcome space is a PMF and when we have a continuous random variable that defines the probability over that variables we call it a PDF. These are both functions in the usual sense of the word and satisfy the following conditions:

The joint, marginal and conditional distributions are represented in the following way (respectively):

The sum and product rules of probability are given respectively as:

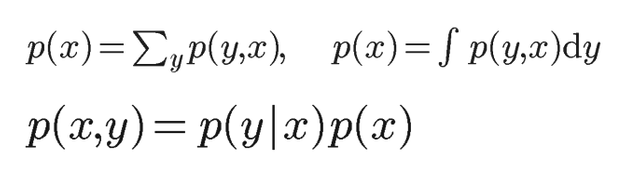
from which Baye's famous rule can be derived. We now introduce further terminology.

• Expectation: This is the average over all values in the domain of the proability function with weightings tied to the individual probabilities. This tells us how likely our belief about the value of a variable is. It is also useful to take the expectation over a whole probability distribution.
• Variance: This tells us how much a variable varies around its expectation value.
• Covariance: This tells us how two varies together, with reference to the expectation of their means.

The following equations express the expectation, variance and covariance respectively. 

Thanks for your attention. Next time more on probability theory. We are aiming to construct a linear regression model in the Bayesian framework, which is one of the cornerstones of ML.