Learn With Steem; Learn How to Calculate the Conventional Cashflow Techniques - NPV (Final Edition) #burnsteem25
Introduction
In my previous posts here and here, I spoke about ARR- Accounting Rate of Return and Payback Period (PBP) as conventional cash flow techniques.
The final technique under this category that I would be explaining with workable examples for a better understanding of them is NPV.
Net Present Value (NPV)
.png) Link
LinkNPV is defined as the difference between the present value of cash inflows and the cash outlays.
It's the summation of all the discounted cash flowing in over a given time frame less the cash flowing out of a proposed project or investment.
This NPV is a capital budgeting technique that's used to analyze the profitability of a project. That is to know if a proposed project is worthy of venturing into or not.
Another term that can be used to relate to NPV is Net Present Worth (NPW). It's the present worth of a project investment.
.jpeg)
Link
NPV generally, is also regarded as a means to measure revenue generation to its discount rate.
One important factor of NPV is that it's used by project evaluators to determine the worth of a business. Any decisions are taken by the company after computation is reliable.
Merits of NPV
.png)
Link
There are so many advantages of using this technique. The results gotten from applying this technique are so much reliable. Some of its advantages are;
It considers the time value of money. This is a constant factor in all NPV evaluated projects.
It recognizes all the cash inflows as they come in whether it's a profit or a loss to the company in question.
The rejection and acceptance decisions under the method are very clear and concise. It gives results in absolute terms.
The NPV of a project is calculated based on cash profits other than accounting profits during evaluation.
The cost of capital used in calculating is a market discount rate and it's higher than any other rate that exists.
For a project to be selected, the benchmark for selection is based on the net present value (if it's a profit).
Through the cost of capital, can be used to avert possible risks associated with the project during investment analysis.
This technique is used to determine the profitability of a given project to determine whether or not the project is worth continuing.
Demerits of NPV
.jpeg)
Link
One thing to note in this NPV technique is that the advantages outweigh the disadvantages. However, for a thing to exist, it must have advantages and disadvantages.
The disadvantages of NPV are;
It's usually too much to calculate the discount rate and can't be easily interpreted by the layman.
it's difficult when to choose a suitable cost of capital to evaluate the project.
Selecting the best NPV out of numerous ones for mutually exclusive projects is usually difficult to determine.
The result gotten from calculating the NPV is used in the currency rate. However, percentage rates are easier to understand.
Decision Rule in NPV
Accept NPV
If NPV is ≥ 0, accept the project because a positive NPV indicates that the project is expected to add value to the firm when ventured into.
Reject NPV
If NPV is < 0, reject the project because a negative NPV indicates that the project would incur losses to the firm when ventured into.
For Independent Projects
For independent projects, accept all projects with positive NPVs subject to available funds.
For Mutually Exclusive Projects
For mutually exclusive projects, accept the project with the highest NPV and reject every other one therein.
Formulas To calculate NPV
Formula 1
NPV =
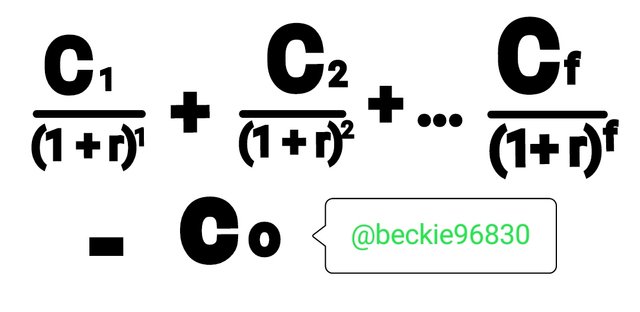
Or
Formula 2
NPV =
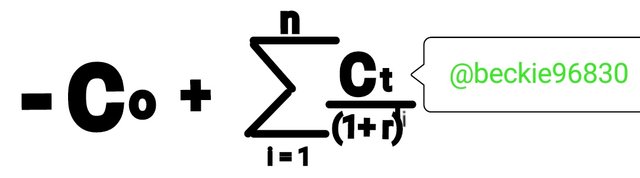
Where;
C1 - Cf represents series of cash inflows year 1,2....f
r represents discount rate
Co represents initial investment
f and t represents time
Debrief
Capital outlay is subtracted from the sum of discounted cash inflows, NPV results should be positive for the project to be considered worthwhile.
A zero NPV means that the invested project repays the original investment plus the required cost of capital with no profit incurred. All debt and capital have been duly paid for.
A negative NPV means that the present value of the cost of the project is more than the present value for f the revenues within an assumed rate of discount and as such, the project shouldn't be accepted.
A positive NPV is a clear indication that the project is viable and worthwhile. It should that the investment is worth undergoing.
Illustration 1
Steemit enterprises has a plan of committing its capital amounting to #1,200,000 on a prospective project.
The firm's cost of capital is 10% while its expected cash inflows are shown in the table below;
| Year | Cashflows (#) |
|---|---|
| 1 | 250,000 |
| 2 | 350,000 |
| 3 | 550,000 |
| 4 | 400,000 |
| 5 | 350,000 |
Required;
Compute the NPV of the project and advise Steemit enterprises on whether to accept or reject the project.
Solution
Discount rate = 10% = 0.1
| Year | Cashflow (#) | Discount @ 10% | Present Value (#) |
|---|---|---|---|
| 0 | (1,200,000) | (1+ 0.1)^0 = 1.0000 | (1,200,000) |
| 1 | 250,000 | (1+ 0.1)^-1 = 0.9092 | 227,275 |
| 2 | 350,000 | (1+ 0.1)^-2 = 0.8264 | 289,240 |
| 3 | 550,000 | (1+ 0.1)^-3 = 0.7513 | 413,215 |
| 4 | 400,000 | (1+ 0.1)^-4 = 0.6830 | 273,200 |
| 5 | 350,000 | (1+ 0.1)^-5 = 0.6209 | 217,315 |
Summation PV = 227,275 + 289,240 + 413,215 + 273,200 + 217,315 = #1,420,245
Net present value = #1,420,245 - (#1,200,000) = #220,245
Recommendation; Steemit enterprises should accept the project because it produced a comfortable NPV of #220,245.
NPV in the case of Annuity
A set of cash inflows that is regular and equal at every period is called an annuity. The process of calculating the NPV of a project that has equal series of cash inflows can be shortened.
The cash flow in the NPV formula will be represented as one and the present value of the Annuity will be denoted as PVAF (n,r).
Formula : NPV = PVAF (n,r) - Cfo
Where:
PVAF = Present Value of an Annuity Factor.
n = Number of years
r = cost of capital
Cfo - Initial Cash Outlay
Illustration 2
Consider a project with the following cash flow details assuming the cost of capital is 10% and advise appropriately.
Solution
Discount rate = 10% = 0.1
| Year | Cashflow (#) | Discount @ 10% |
|---|---|---|
| 0 | (800,000) | (1+ 0.1)^0 = 1.0000 |
| 1 | 400,000 | (1+ 0.1)^-1 = 0.9092 |
| 2 | 400,000 | (1+ 0.1)^-2 = 0.8264 |
| 3 | 400,000 | (1+ 0.1)^-3 = 0.7513 |
| 4 | 400,000 | (1+ 0.1)^-4 = 0.6830 |
| Total | - | 3.1698 |
NPV = PVAF(n,r) - Cfo
#400,000(4,10) - 800,000
(4,10) = 3.1698
NPV = (#400,000 × 3.1698) - #800,000
NPV = #1,267,960 - #800,000 = #467,960
Recommendation; The project should be accepted because it produced a comfortable NPV of #467,960.
Conclusion
I hope this lesson can give a basic understanding of how to compute the net present value of a project.