[ADK] 코인 백서 한글판 - 3장~10장
안녕하세요. @vincentkang 입니다.
ADK 코인 백서(Draft) 한글판이 완성되어 나머지 부분 공개드립니다.
번역에 힘써주신 분들에게 다시 한번 감사드립니다.
이전 내용은 아래서 참조부탁드립니다.
https://steemit.com/kr/@vincentkang/2wlgqo-adk 서론 ~ 1장
https://steemit.com/kr/@vincentkang/adk-2 2장

<아이도스 퀴네에 백서 한글판(Draft)>
역자: 블록체인 가치투자, sasa,
아이돗, hanumanbanana,
케빈, 1q2w3e4r, ctkim,
청구삼촌, 텐베거, ryan
검수: ADK 한국인 투자자 모임
3장 Signature Scheme(서명 방식)
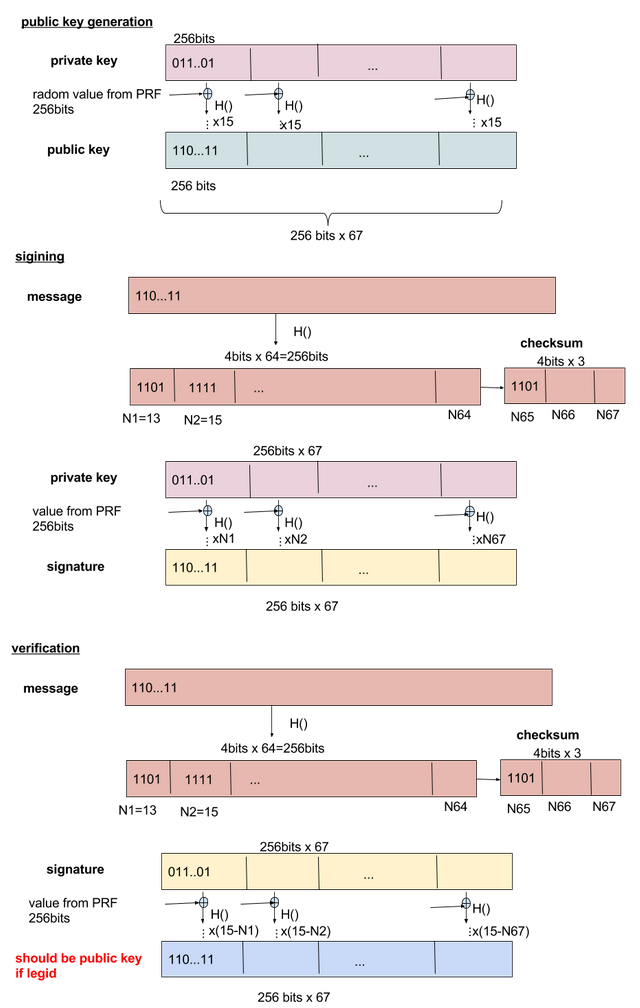
그림1: wots+ 서명에 의한 키의 생성, 서명, 검증.
서명방식으로 XMSS를 채용했으며 패러미터는 IETF의 RFC 드래프트에 기재된 설정을 사용하고 있습니다. XMSS는 빈터니츠 원타임 서명(WOTS+: Winternitz One Time Signature)에 기초를 두고 있습니다. 그림1은 공개 키의 생성방법, 메시지의 서명방법, 그리고 서명의 검증방법을 설명하고 있습니다.
67개의 32바이트 길이(256bit) 랜덤 이진수 값을 비밀 키 로 부르겠습니다. 공개 키를 만들려면, 각 32바이트 길이의 이진수 데이터
를 SHA256으로 16회 해시화 해야 합니다. 해시화를 진행하기 전에 PRF(유사 난수 함수)로부터 생성된 값과 랜덤 이진수 데이터의 XOR(배타적 논리합)을 취합니다. 이 처리야말로 보안 레벨을 그대로 유지하면서도 서명 사이즈를 줄이는 비결입니다. 이로서 67개의 32바이트 길이 이진수 데이터가 생성 가능해집니다. 이것이 공개 키
입니다.
서명에 관해 설명드리자면, 먼저 메시지를 한 번 SHA-256으로 해시화하여 얻어낸 256bit 데이터를 4bit 64개의 이진수 문자열로 분할합니다. 또한 해시화 한 매시지로부터 16bit의 체크섬을 계산하여 4개의 4bit 이진수 문자열로 분할합니다. 이로서 (64+4)개의 4bit 이진수 문자열을 얻을 수 있습니다. 위의 그림에선 이러한 값을 등으로 나타내고 있습니다. 비밀 키
에서 공개 키 생성시에 사용한 난수로 배타적 논리합을 제거한 뒤
회 해시화하여 서명
를 얻습니다.
이 체크섬은 악의를 가진 메시지로부터 온 공격을 방어하기 위해 사용됩니다. 예를 들어, 공격자가 000....0의 해시를 가진 메시지를 체크섬 없이 생성할 경우 때, 서명이 체크섬 없이는 비밀 키와 일치해버리는 경우가 발생하여 공격자가 비밀 키를 알수 있게 되어버리고 맙니다.
서명의 확인에 관해선, 서명 생성과 같이 메시지로부터 를 계산해냅니다. 그리고 서명
를 공개 키 생성시에 사용한 난수로 배타적 논리합을 제거한 후, 해시화를 (
회 반복하여
를 얻습니다. 그후
가 공개 키
와 일치하는지를 확인합니다.
추가적으로, WOTS+의 공개 키는 단 한 번만 사용할 수 있다는 것을 기재해두겠습니다.
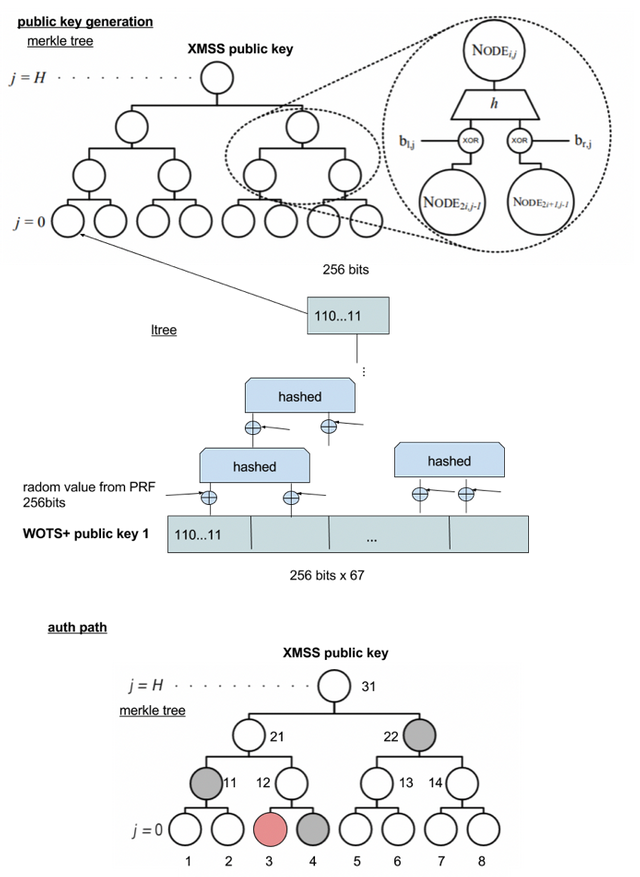
그림2: XMSS의 키 생성과 인증 경로(auth path)
그림2는 XMSS에 의한 키 생성방법을 나타내고 있습니다. 간단히 설명하자면, XMSS는 하나의 비밀 키로부터 만들어지는 모든 공개 키를 모아 머클 트리(Merkle Trees)라고 불리는 트리 구조를 구축한 것입니다. 고로, 하나의 공개 키를 몇 번이든 사용할 수 있습니다.
먼저, 복수의 비밀 키 와 그에 대응하는 WOTS+ 공개 키
를 만들 필요가 있습니다. 이때, 하나의 'ltree'는 이러한 공개 키 중 하나를 해시화함으로서 만들어집니다. 공개 키 하나가 즉 67개의 32bit 이진수 데이터라는 사실을 떠올려주십시오. 공개 키의 67개 이진수 데이터에 대해 인접한
을 반복하여 결합해 해시화함으로서 최종적으로 32바이트의 이진수 데이터를 얻을 수 있습니다. ltree 작성을, 공개 키의 갯수
만큼 반복합니다. 즉,
(
:머클 트리의 층수|height)만큼 반복합니다. 이러한 것이 머클 트리의 말단(leaves)입니다. 머클 트리의 루트 해시는 ltree와 같은 방법으로 ltree의 루트를 해시화 함으로서 얻을 수 있습니다. 이 루트 해시가 XMSS의 공개 키입니다.
서명에 관해선, 이전에 사용되지 않은 비밀 키와 대응하는 공개 키를 골라 WOTS+서명을 얻습니다. XMSS 서명은 WOTS+서명에 인증 경로(auth path)가 추가된 것입니다.
인증 경로는 머클 트리의 루트 해시를 계산하기 위한 추가 해시 데이터입니다. 예를 들어 그림2의 3번 비밀 키와 공개 키를 서명에 사용한다고 합니다. 이때, WOTS+서명으로부터 3번 공개 키를 계산해낼 수 있습니다. 3번의 해시 데이터는 이미 존재하고 있습니다만 12번의 해시 데이터를 얻기 위해선 4번의 해시 데이터가 필요해집니다. 고로 인증 경로에는 4번의 해시 데이터가 필요합니다. 똑같이, 31번의 루트 해시(즉 XMSS 공개 키)를 얻기 위해선, 4번, 11번, 22번의 해시 데이터가 필요합니다.
검증시에는 WOTS+서명과 인증 경로를 사용하여 머클 트리의 루트 해시를 계산함으로서 루트 해시가 XMSS 공개 키와 일치하는지 확인합니다.
추가적으로 아래와 같은 특징이 있습니다.
- 서명자는 어떤 비밀 키가 이미 사용되었는지를 기억해야만 합니다. 동일한 비밀 키는 사용할 수 없습니다.
- 공개 키는 32바이트의 유사 난수의 시드로 32바이트의 머클 트리의 루트로부터 구성됩니다. 지금까지 설명한 유사 난수는 모두, 이 32바이트의 유사 난수 시드로부터 생성됩니다.
- 서명의 키 사이즈는 약 3KB입니다.
- SHA256 해시는 역상 저항성을 가지고 있으며, 해시의 출력 값으로 입력 값을 특정하는 건 지극히 어렵습니다. 만일 양자 컴퓨터를 사용해도 공개 키로부터 비밀 키를 밝혀내는 건 어렵습니다.
그리고, 만일 (머클 트리의 층수|height)를 더욱 늘리면 공개 키도 복수 회 사용 가능해집니다만, 이 경우는 최초의 공개 키 생성에 시간이 걸리게 됩니다.
표1: 키 생성과 XMSS 사용시에 관한 머클 트리의 층 별 싱글코어당 추정 소요 시간.
| 층수(높이) | 키의 갯수 | 키 생성시간 | 이용자 |
|---|---|---|---|
| 1 | 1 | 1초 미만 | 일회성 유저 |
| 10 | 1,024 | 수 초 | 일반 유저 |
| 16 | 65,536 | 수 분 | 기업 |
| 20 | 1,048,576 | 약 30분 | 대기업 |
표1에 4종류를 표시하고 있습니다. 매번 주소를 바꾸거나 1000번이나 코인을 송금하지 않는 일반 유저는 공개 키 생성에 계산량이 적은 height 10을 사용합니다. 하나의 공개 키로 몇 번이나 코인을 송금해야 하는 기업과 사업주는 height 16과 20을 사용합니다. 여기서 유의해야 할 점은 [2]에서 언급하고 있는 의 경우 생성시간은 짧지만 XMSS에 비해 서명 데이터의 사이즈가 약 40KB나 되어 매우 크기 때문에 실제로 이용할 수 없다는 것입니다.
4장 iMesh
4장 iMesh
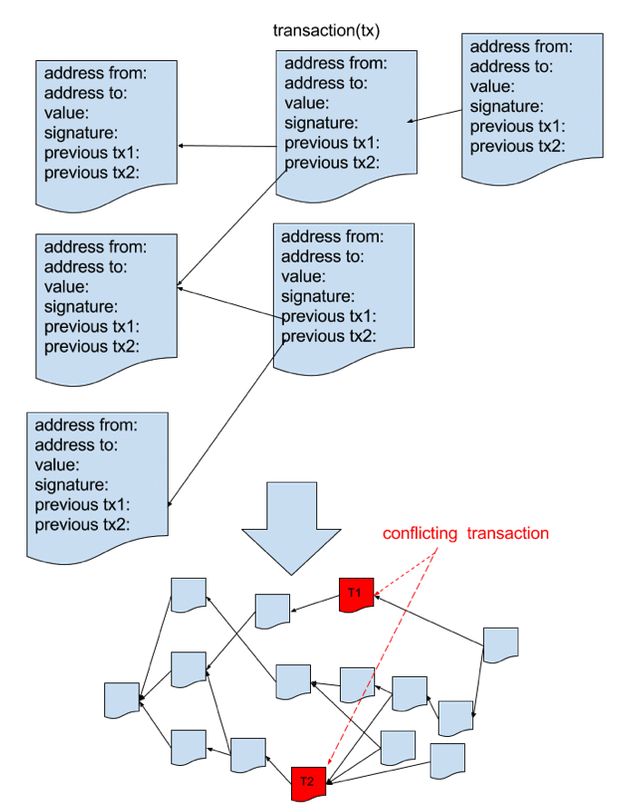
그림3:iMesh
코인 송신자가 트랜잭션을 보낼 때, 해당 트랜잭션에는 이전에 승인된 복수의 트랜잭션이 직접적으로 포함됩니다. 그림3은 저희가 라고 부르는 트랜잭션의 DAG 구조를 나타내고 있습니다. iMesh는 송신자가 DAG의 말단 트랜잭션(어느 트랜잭션에도 참조되지 않은 트랜잭션)와 parent 트랜잭션이 유효한지 아닌지 확인하여 개중 유효한 것을 선택합니다. 최종적으로 송신자는 이 유효하다고 확인된 트랜잭션을 송신자의 트랜잭션에 포함시킵니다.
비트코인 등 블록체인에 기초한 암호화폐에 이용되는 블록은 바로 이전의 블록을 참조하기에 하나의 선과 같은 구조를 띄게 됩니다. 하지만 DAG구조는 한 개의 트랜잭션으로 많은 블록을 참조할 수 있습니다. 블록체인은 일정시간마다 한 블록씩만 성장하지만, 그에 비해 DAG는 많은 트랜잭션이 일제히 성장합니다. 즉, DAG는 블록체인보다 스케일러비티가 뛰어나다고 할 수 있습니다.
하지만, 트랜잭션 사이에 충돌이 일어날 경우 DAG의 스케일러비티 상의 이점이 예상치 못한 부작용을 일으킬 수 있습니다. 예를 들어 어드레스A에 10개의 코인이 있고, A가 B에게 10개의 코인을 송신하는 트랜잭션을 T1, A가 B에게 10개를 송신하는 또 하나의 트랜잭션을 T2라고 하겠습니다. 이로 인해 Address A에 2개의 충돌하는 트랜잭션이 발생합니다. 블록체인에 기초한 암호화화폐의 경우, 한 쪽(T1)이 블록에 보존되면, 다른 한쪽(T2)은 절대 블록에 보존되지 않습니다. 즉, T2는 유효한 트랜잭션이 아니게 됩니다. 한편, DAG의 경우 충돌한 트랜잭션(그림3에서 빨간색으로 표시한 부분) 중 어느 쪽이 유효한 트랜잭션인지 판단하는 건 매우 어렵습니다. 이 문제를 해결하기 위해 저희는 'SPECTRE'[9]의 투표 메카니즘을 이용합니다. 이로서 아무런 근거 없이 코인을 만들어낼 수 없어지기에 공격자는 위에서 언급한 '이중지불(double spending)'을 포함한 어떤 공격도 시도할 수 없게 됩니다.
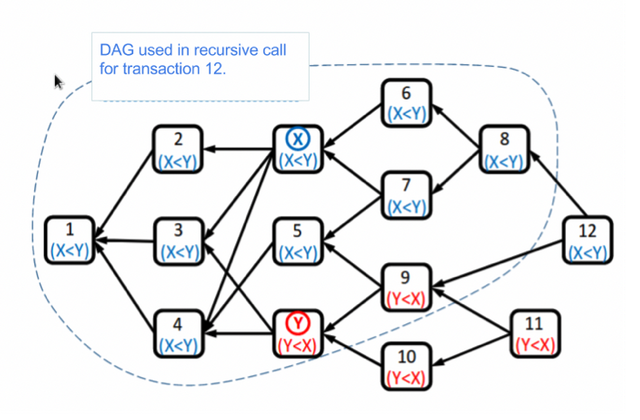
그림4. 간이 DAG상의 투표 순서 예시
SPECTRE는 각각의 충돌한 트랜잭션에 대해, 충돌한 트랜잭션에게 투표한 트랜잭션의 수를 계산합니다. 그림4는 투표 순서를 나타냅니다. 이 그림에선 트랜잭션 x와 y가 충돌하고 있습니다. 트랜잭션x와 트랜잭션6~8은 자신의 과거 이력에 y가 아닌 x를 가지고있기 때문에 트랜잭션 x에게 투표합니다. 마찬가지로, 트랜잭션 y와 트랜잭션 9~11는 y에 투표합니다. 트랜잭션12는 트랜잭션10, 11, 12를 포함하지 않는 DAG상의 재귀 호출(recursive calling)에 따라 투표를 시행합니다. 트랜잭션 1~5는 후속 트랜잭션 중에서 y의 투표자보다 x의 투표자가 많다는 사실에 기초해 x에게 투표합니다. 결과로서 x의 투표자가 y보다 많음으로 x가 정당하다고 판단되는 것입니다.
DAG의 기하학적 관점으로부터, 어째서 투표로 정당한 트랜잭션이 결정되는지 해설하겠습니다.
- 트랜잭션 x를 parent로 둔 트랜잭션은 트랜잭션 x에게 투표합니다. 정당하게 생성된 트랜잭션은 익명의 트랜잭션 집단에게 투표받음으로서 계속해서 새로운 후속 트랜잭션을 생성해냅니다.
- 어떤 트랜잭션이 x와 y를 parent로 두고 있을 때, 해당 트랜잭션은 투표자가 많은 쪽에 투표합니다. 새로운 트랜잭션이 투표에 참가함으로서 이전의 투표결과에 따르고 해당 투표를 강화하여 다수파를 최대화하는 것을 보증합니다.
- 어떤 트랜잭션이 x나 y중 어느 쪽도 parent로 두고 있지 않을 경우, 해당 트랜잭션은 투표자 다수가 있는 쪽의 트랜잭션에 투표합니다. 이 규칙에 의해, x의 parent(더욱 나아가 x의 children)가 y에 투표하는 표에 반대하여 x의 표수를 확대시키는 것이 가능합니다. 이는 만에 하나 y가 장시간 숨어있을 경우 대비한 것입니다. 즉, 프리마이닝 공격법(공격자가 트랜잭션을 스팸하여 큰 트랜잭션 덩어리를 네트워크에 들키지 않게 만들어두는 공격 방식)을 막는 대항수단입니다.
- x가 y의 parent인 경우, 모든 블록이 만장일치로 x를 투표합니다.
여기서 주목해야 할 점은, SPECTRE가 33%가 아닌, 50%의 연산력 공격을 버텨낼 수 있다는 사실입니다.
비트코인과 같이 송신자는 트랜잭션이 충분한 수의 다른 트랜잭션에게 확인될 때까지 기다려야만 합니다. 문헌[9]에서는 얼마나 오래동안 수신자가 기다려야만 하는지 언급하고 있습니다. 5컨펌을 기준으로, 비트코인 네트워크 안에서 공격자가 30%의 해시파워를 가지고 있다고 가정한다면, 공격자의 비트코인 네트워크 공격 성공 가능성은 17.8%[1]입니다. SPECTRE의 투표 방식을 사용할 경우 동등한 성공률(17.8%)을 얻기 위해선 130개의 참조 트랜잭션이 필요합니다. iMesh의 트랜잭션 속도가 빨라짐다면 수신자의 대기시간은 더욱 짧아집니다. 허나 그 말은 즉, Aidos Kuneen 네트워크가 초기 단계에 머물러있는 동안은 대기시간이 길어집니다. 그리고 공격자가 해시파워의 반 이상을 보유하고 있는 경우, iMesh는 공격받게 됩니다. 즉, 악성 트랜잭션이 부정한 방법으로 승인되는 것입니다. 특히 iMesh에, 소수의 트랜잭션 밖에 없는 극초기 단계에서는 이러한 일들이 일어날 수도 있습니다. 이에 저희는 iMesh의 초기 단계에서도 트랜잭션을 확정적으로 확인할 수 있는 메카니즘을 도입하였습니다. 또 하나, 특기할 사항으로서, iMesh에 많은 말단 트랜잭션이 있을 때 다른 트랜잭션을 참조하고 있는 트랜잭션의 숫자는 적어진다는 사실을 꼽을 수 있습니다. 고로 저희는 얼마만큼의 트랜잭션이 하나의 트랜잭션으로부터 참조되어야하는지에 관해 고려해야 할 필요가 있습니다. 이 문제에 관해선 9장에서 다루겠습니다.
SPECTRE에서는 많은 트랜잭션이 과거의 트랜잭션을 참고하기 때문에 송신자가 가능한 한 많은 트랜잭션을 참조하는 행위에 의의가 발생합니다. 왜냐하면, 트랜잭션의 승인 횟수는 '해당 트랜잭션이 참조하고 있는 트랜잭션의 수'와 '해당 트랜잭션이 장래에 다른 트랜잭션에 의해 참조될 횟수'에 의존하기 때문입니다. 즉, 더욱 많은 과거 트랜잭션을 참조할수록 더욱 빨리 승인되어 수신자에게 확실히 코인을 보낼 수 있게 되는 것입니다. 다르게 말하자면 트랜잭션의 참조수가 적을 경우에는 승인에 시간이 오래 걸림으로 지불이 거부될 수도 있습니다.
5장 Proof of Work(작업 증명)
트랜잭션을 송신할 때 송금자는 비트코인의 채굴자가 하는 것처럼 스스로 작업 증명(PoW)을 진행해야만 합니다.
각 트랜잭션은 논스(nonce: 각 트랜잭션이 한 번만 처리되도록 만들어주는 일종의 카운터) 필드를 지니고 있으며, 트랜잭션의 해시는 특정한 값이 되어야만 합니다. PoW에 걸리는 시간은 대략 5~10분 정도이며 Aidos Kuneen의 작업 증명은 비트코인의 작업 증명에 비해 DDoS 공격 혹은 이중 지불을 방지하는 데에 필요한 작업량이 적습니다.
추가적으로 PoW는 트랜잭션 발생 분포를 분산시킬 수 있습니다. 왜냐하면 이 PoW가 되지 않은 채 다음으로 발생할 트랜잭션의
을 나타내는 난수
의 분산이라 가정하고,
가 PoW의 필요 시간을 나타내는 난수
의 분산이라 가정했을 때,
과
는 독립되어있기에 난수
의 트랜잭션 발생 분포가
이 되기 때문입니다.
고로 우리는 iMesh의 규모가 커졌을 때 PoW 난이도 조절을 고려할 수 있습니다.
PoW에 관해서 말씀드리자면, Aidos Kuneen은 Blake2b-256에 더하여 SHA256 알고리즘을 사용하고 있습니다. 이유는 아래와 같습니다. Aidos Kuneen의 풀 노드는 비트코인의 노드가 여러 트랜잭션이 담긴 블록을 처리하는 것과 달리 모든 트랜잭션의 PoW를 개별적으로 계산하여 처리합니다. 당연히 비트코인에 비해 처리해야 하는 PoW의 양이 많기 때문에 우린 ASIC 방지를 위해 만들어진 고난이도 PoW 알고리즘(cryptonight 및 scrypt 포함)을 사용해선 안 됩니다. 무엇보다, Aidos Kuneen에는 높은 해시 파워를 가짐으로 주어지는 보상이 없습니다. 또한, 해시 파워의 과반수 혹은 전체를 독점한 자가 이중지불 유발을 시도할 수 있기에 ASICs는 Aidos Kuneen의 PoW에 사용되어선 안 됩니다.
그래서 우리는 ASIC가 상대적으로 위력을 발휘하지 못하는 BLAKE2를 선택했고 이는 여타 ASIC 면역 해시들보다 적은 계산력을 요합니다. 추가적으로 저희가 서로 다른 두 가지 해시를 선택한 이유로는 기존의 ASICs나 최신 CPU에 SHA 확장을 사용하는 시도를 방지하기 위해서라는 사실도 알아주셨으면 합니다.
6장 Cooperative Proof of Work(협동 작업 증명)
CPU성능이 낮은 IoT기기 등을 위해 coPoW라 불리우는 협동 작업 증명을 소개하고자 합니다. coPoW는 서로 다른 송신자들의 트랜잭션을 섞을 수 있으며 하나의 트랜잭션을 각각의 송신자가 함께 PoW할 수 있게 되는 것을 의미합니다. coPoW를 이용해 수많은 IoT 기기들을 활용해 PoW를 진행할 수 있습니다.
이 경우 PoW는 분산 합의 알고리듬을 사용해 마치 비트코인 채굴 풀(당구)과 같은 탈중앙화 방식으로 이루어집니다.
- coPoW에 참여하고자 하는 자는 풀노드(full-node)를 통해 네트워크에 요청을 보냅니다.
- coPoW에 참여하고 싶은 자 또는 이미 coPoW를 하고 있는 자가 그 요청에 coPoW 레스폰스를 보냅니다.
- coPoW 네트워크에 참가하여 리더를 선택하거나 Raft 알고리즘으로 누가 리더인지 알아냅니다.
- 트랜잭션을 리더에게 보내고 리더로부터 해당에 연관된 트랜잭션을 받습니다.
- 리더로부터 혼합된 트랜잭션을 받습니다.
- PoW를 시작합니다.
- 주기적으로 목표치보다 큰 값을 가진 PoW 결과를 리더에게 보냅니다.
- 주기적으로 리더로부터 그룹의 PoW 결과를 취득합니다.
- 리더는 일정 주기 안에 결과를 보내지 않은 자나 틀린 결과를 보낸 노드를 거부합니다. 이러한 경우에는 리더가 그룹의 구성원들에게 coPoW를 재시작하도록 지령을 내립니다.
- 틀린 결과를 보낸 자는 그룹을 나가게 됩니다.
- (목표치와 일치하는)유효한 결과를 수신하면 PoW를 중지합니다.
추가적으로 그룹의 구성원은 익명성을 위해 Tor를 사용할 수도 있습니다. coPoW 그룹에 속한 파티들은 주기적으로 목표보다 간단한(PoW의 목표치) 결과(트랜잭션의 nonce)를 보내야 합니다. 이는 coPoW에 참여했지만 실제로 작업 증명을 하지 않는 무임 승차를 예방하기 위해서입니다. Aidos Kuneen의 증명 목표치는 가변적입니다. 예를 들어, 성능이 매우 낮은 CPU를 가진 IoT 장비 그룹은 증명 목표치를 로 설정할 수 있으며 일반적인 컴퓨터의 경우
로 설정 가능합니다.
7장 AKShuffle
익명성을 보증하기 위해 저흰 AKShuffle이라는 기술을 사용합니다. AKShuffle에는 익명성을 확보하기 위해 송금에 영지식 비대화형(ZKNI) 증명이 이용되고 있습니다. ZKNI에 의해 누구든 자신의 값을 밝히는 일 없이도 자신이 몇몇 함수를 만족시킨다는 사실을 증명할 수 있습니다. 예를 들어 앨리스가 암호화 함수 에 대해 입력값
를 암호 키
로 입력하여 입력값
가
를 출력, 즉
라고 가정하고, 밥이 앨리스가 실제로
가
를 피드백하는
를 가지고 있는지 알고 싶어한다고 가정하겠습니다. 하지만 앨리스는 그녀의
를 밝히고 싶어하지 않습니다. ZKNI는 이러한 목적을 위해 존재하는 기술입니다.
우린 ZKNI를 실제 사용함에 있어 앞서 [8]에서 언급한 ZKBoo(ZKB++)를 이용합니다. ZKBoo는 양자내성(역자 주: 양자 컴퓨터에 대해 내성이 있는 암호 방식)을 가진 해시와 암호화 함수(AES)만을 사용합니다.
그림 5
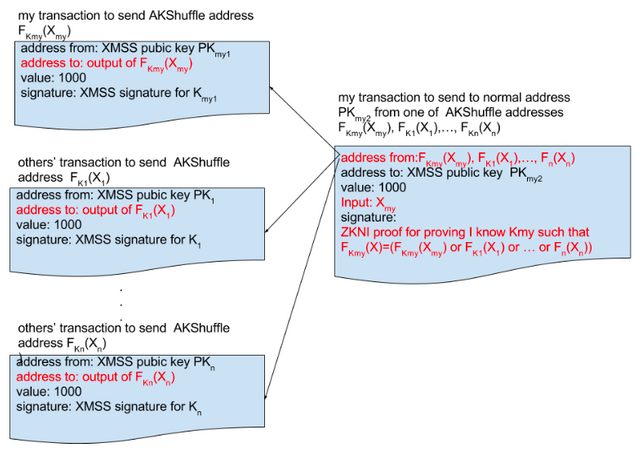
그림 5는 AKShuffle에 관한 트랜잭션을 해설하고 있습니다. 암호화폐를 셔플하고 싶어하는 홍길동은 자신의 ADK 코인을 셔플 어드레스로 전송합니다. 셔플 어드레스는 암호 키 와 암호화 함수
의 출력입니다.
는 홍길동의 비밀 키이며,
는 그의 공개입력으로, 다른 누군가가 셔플 어드레스에서 출금할 때에 사용합니다.
그후 잠시 후에 홍길동은 셔플된 암호화폐를 회수합니다.
홍길동은 그의 보통 어드레스 (홍길동의 XMSS 공개 키)로 보낼 하나의 트랜잭션을 작성합니다. 그 트랜잭션은 타인의 AKShuffle 어드레스
와 자신의 AKShuffle 어드레스
를 섞어서 인풋 어드레스로 이용합니다. 이것은 즉, 어느 어드레스가 실제로 지불에 이용되었는지는 외부에선 알 수 없다는 뜻입니다.
서명에 있어 홍길동은 ZKNI 증명을 만족시킴으로서 트랜잭션에 포함된 AKShuffle 어드레스 중 하나가 의 출력과 같아지도록 하는
를 알고 있음을 증명합니다. iMesh에선 AKShuffle의 어드레스
가 한 번이라도 이용된 사실이 기록되어있기에 어드레스가 재이용되는 일을 방지하고 있습니다. 고로 트랜잭션에는 공개 입력
가 포함되어있습니다.
트랜잭션에 포함되는 값은 늘 같아야만 한다는 사실에 주의해주시기 바랍니다.
또한 AKShuffle의 서명방식과 일반 지불의 서명방식이 다르다는 사실에도 주의해주십시오. AKShuffle(ZKBoo)는 누군가의 ADK 코인을 셔플할 때에만 이용됩니다. 즉 AKShuffle을 다른 누군가에게 ADK 코인을 지불할 때에 사용할 수는 없습니다. 이는 ZKBoo의 시그니처 사이즈가 크기 때문입니다(입력 어드레스의 수가 다섯일 경우 약 500KBytes에 달합니다).
8장 Network
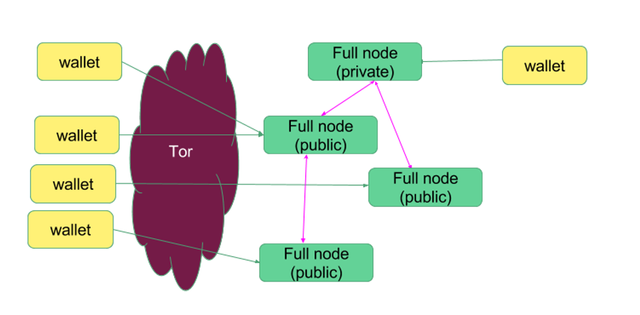
그림6: Aidos Kuneen의 풀 노드와 클라이언트(월렛)
Aidos Kuneen의 네트워크는 풀 노드를 동반한 P2P 형식으로 구축되어 있습니다. 클라이언트는 이러한 풀 노드 또는 자기 소유의 풀 노드에 접속하여(통상적으론 지갑 어플리케이션을 통해) 트랜잭션을 전송하기 위한 API를 보낼 수 있습니다. 풀 노드 간 트랜잭션의 송수신에는 비트코인 등이 사용 중인, 패킷 사이즈를 삭감하기 위해 가변 길이 정수 방식(variable length integer scheme)을 포함한 프로토콜을 사용하고 있습니다.
공개된 풀 노드와 클라이언트 사이의 접속에는 익명성을 위해 Tor가 사용되고 있습니다만, 송수신 속도가 중시되는 풀 노드 간 접속에는 Tor가 사용되지 않습니다. 풀 노드 간 송수신에서는 트랜잭션이 풀 노드에게 중계됨으로 인해 네트워크상의 트랜잭션을 누가 전송했는지 알 수 없기 때문에 익명성을 추가적으로 확보할 필요는 없게 됩니다. 한편 풀 노드는 클라이언트의 IP주소와 클라이언트가 무엇을 송신했는지 알 수 있습니다.
또한, 우리는 피어 검색을 위해 Kademlia 네트워크를 구축하고 있습니다. 현재 Kademlia에서 DHT 방식은 사용되지 않지만, 가까운 시일 내에 독자적인 익명 네트워크를 구현할 때 트랜잭션 분산 저장을 위해 Kademlia를 이용할 예정입니다. 유감스럽게도 Tor에 양자 연산 내성은 없습니다 Tor는 다수의 사용자를 확보하고 있기에 이들로부터 강력한 익명성을 확보할 수 있습니다. 또한 장래엔 Aidos Kuneen 사용자가 많아져 독자적인 익명 네트워크를 구축할 수 있게 됩니다.
저희는 분산 트랜잭션 유지를 통한 트랜잭션 분산화 역시 계획중입니다(이는 각각의 풀 노드가 모든 트랜잭션을 담게 하는 것이 아니라 풀 노드끼리 서로 다른 풀 노드가 가지지 않은 트랜잭션을 공유하는 방식이며, 이를 통해 보다 높은 확장성을 기대할 수 있습니다). 현재 지속적으로 개발하고 있습니다. 표2는 패킷의 명령어를 나타내고 있습니다.
표2: 표준 패킷 명령어
| command | description |
|---|---|
| ping | ping to another node |
| pong | resoponse of ping |
| find_node | requests node infos |
| resp_node | response node infos |
| req_transactionequests transactions contents with hashes | |
| resp_transactions | responds transactions contents |
| req_leaves | requests leaves’ hashes |
| resp_leaves | responds leaves’ hashes |
| invent | invent a new transaction hash |
| ack_invent | ack of invent |
| invent_coPoW | invent nodes are searching for coPoW |
| ack_coPoW | ack of invent_coPoW |
| find_value | reserved for future use. |
| store_value | reserved for future use. |
9장 Leaves in Mesh(말단 트랜잭션)
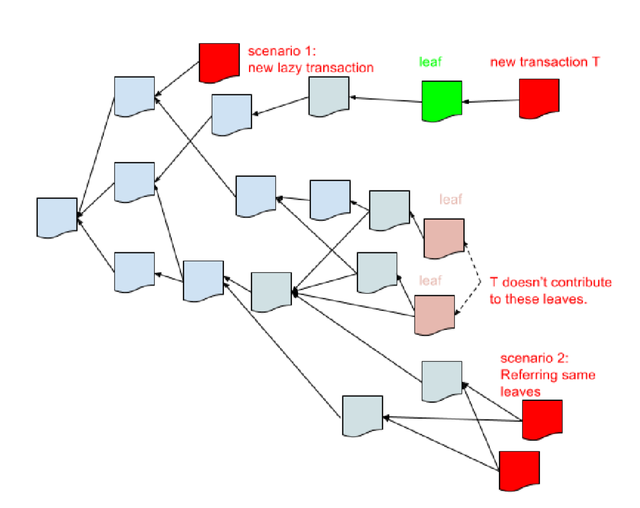
그림7: iMesh의 말단 트랜잭션
Section 4에서 언급한 것처럼, iMesh상에서의 트랜잭션 승인 속도는 말단(leaves)의 수에 의존하게 됩니다. 이는 많은 말단 트랜잭션이 존재할수록 하나의 트랜잭션이 다른 트랜잭션에게 참조될 확률이 낮아지기 때문입니다(그림7). 하지만 말단 트랜잭션이 증가할 가능성이 있는 몇 가지 시나리오가 있습니다.
첫 번째 시나리오는, 비협조적인 송신자가 의도적으로 자신의 트랜잭션으로 비 말단 트랜잭션(non-leaves)을 참조할 경우 말단 트랜잭션이 줄어들기는 커녕 오히려 하나 늘어나게 됩니다. 하지만 이 송신자는 자신의 비협조적인 행동을 후회하게 될 것입니다. 왜냐하면 앞서 말했듯이 승인에 걸리는 시간은 송신자의 트랜잭션이 참조하고 있는 트랜잭션의 수에도 의존함으로 송신자가 의도적으로 비협조적인 행동을 취하고 있다고 판단될 경우 수신자가 지불을 거부하기 때문입니다.
두 번째 시나리오는, 어떤 트랜잭션 T1가 iMesh에 들어왔을 때 마침 또 다른 트랜잭션 T2가 PoW 진행중이고, T1와 T2가 모두 같은 트랜잭션을 참조해버린 경우입니다. 이러한 경우에도 말단 트랜잭션의 숫자는 증가하고 맙니다. 이 시나리오는 송신자의 의도와 상관없이 우연히 일어나기에 피할 수가 없습니다.
세 번째 시나리오는, 공격자가 많은 트랜잭션을 브로드캐스트하는 행위를 통해 대량의 말단 트랜잭션을 발생시켜 승인을 지연시키려 하는 경우입니다. 이러한 시나리오는 PoW를 통해 어느 정도 저지할 수 있지만, 여전히 발생할 가능성이 있습니다. 한편으론 트랜잭션 하나 당 참조하는 트랜잭션의 수가 늘어나기에 이것이 말단 트랜잭션의 감소(iMesh의 수렴)에 도움을 줄 것으로 기대할 수 있습니다. 하지만 이로서 트랜잭션의 사이즈가 늘어나게 됩니다. 저희는 iMesh를 수렴시키기 위한 최적의 수치를 구해야만 합니다.
트랜잭션 수신의 과정은 푸아송 과정으로 모형화가 가능하다고 가정하고 있습니다. 그리고 PoW의 완료시간은 지수분포로 모형화 할 수 있음으로 와
를 각각 푸아송 과정의 레이트와 지수분포의 기대치라고 했을 때, 송신자는 자신의 트랜잭션을
의 레이트로 생성하고 트랜잭션을 참조하는 시간까지 합하여 평균적으로
로 PoW를 완료하게 됩니다. PoW를 진행하는 중에도 다른 송신자 역시 트랜잭션을 생성하고, 같은 트랜잭션을 참조하고 있을지도 모릅니다. 시각
일 때의 말단 트랜잭션 수는 시각
의(즉, 시간 경과에 따라 변동하는) 말단 트랜잭션 수에 의존하고 있음으로 말단 트랜잭션의 수를 나타내는 식을 푸는 건 어렵습니다. 고로, 저희는 말단 트랜잭션의 움직임을 시뮬레이션하였습니다.
Algorithm1은 iMesh 상의 말단 트랜잭션 수를 시뮬레이션하는 알고리즘을 나타냅니다. = 10minutes(평균 10분으로 PoW가 끝난다는 걸 뜻합니다)로 고정하고 하나의 트랜잭션 내의 참조 트랜잭션 수를
=2, 4, 8, 16, 32라고 하겠습니다. 이상의 조건으로 4종류의
를 시뮬레이션해보겠습니다.
- 분당 1 트랜잭션 (1tx/min)
iMesh의 초기단계:트랜잭션이 서서히 iMesh 안에서 생성됩니다. - 매초 1 트랜잭션 (1tx/sec)
- 매초 5 트랜잭션 (5tx/sec) ※2017년 5월의 Bitcoin 초당 트랜잭션 최대치.
- 매초 10 트랜잭션 (10tx/sec)

부록의 그림 8~12에 시뮬레이션 결과를 첨부합니다.
=1 tx/min에 대한
=8, 16, 32의 결과에 관해선
=4의 결과와 유사하기에 생략하겠습니다. 이러한 결과로부터 판단하건데, 말단 트랜잭션의 수는
의 수에 거의 비례하여 감소합니다.
= 1 tx/min 그리고
=2로 두었을 경우 역시 DAG를 수렴시키기엔 충분하지 않습니다(#leave=3-26).
=4라면 비교적 낫습니다(#leaves=1-18). 다른
에 관해선
=2가 기타
보다 확연히 나쁩니다. 예를 들어
TPS고
라면
,
라면
입니다. 만일 iMesh에 비트코인과 동일한 속도로 트랜잭션이 들어온다고 가정한다면
를 사용해선 안됩니다.
위의 케이스에서 하나의 트랜잭션에 대해 그 트랜잭션을 참조하는 트랜잭션의 수가 어떻게 늘어나는지도 시뮬레이션하였습니다. 그림 13~16에 결과를 첨부합니다.
이 여러 장의 그림에선 X축이 iMesh가 안정된 이후에 iMesh에 추가된 트랜잭션의 수를 나타내며 Y축이 어떤 무작위 트랜잭션을 참조하고 있는 트랜잭션(child 트랜잭션)의 참조수 를 나타내고 있습니다. 그래프는 이상적으로는 대각선을 이루게 됩니다.
=1 tx/min일 경우의 임의의
그래프는 거의 대각선이 됩니다. 하지만
가 증가하면
가 적어집니다. 예를 들어
TPS일 때
는
로 25000 트랜잭션 이후(즉 평균
)에도 대각선이 되진 않습니다.
일 땐 4000 트랜잭션 이후(즉 평균
)에 1차 선형으로 증가하기 시작합니다.
저희는 하나의 트랜잭션을 참조하는 child 트랜잭션의 참조수를 변수로 두고, 현재는 디폴트 값을 8로 설정해두기로 하였습니다. iMesh가 비트코인의 최대 TPS(Transactions Per Second)인 매초 = 5tx/sec까지 성장하더라도
=8라면 iMesh는 #leaves=500 부근에서 문제 없이 수렴됩니다. 그리고
=8나 된다면 공격자가 말단 트랜잭션을 늘리려 하는 시도 역시 막을 수 있습니다. 공격자가 전체 해시파워의 절반을 보유하고 있다 해도 추가할 수 있는 말단 트랜잭션은 아무리 많아도 트랜잭션 하나 당 한 개 정도입니다. 정당한 트랜잭션이 8개의 트랜잭션을 참조한다면 매초 40개의 말단 트랜잭션이 참조될 것임으로 공격자의 말단 트랜잭션 역시 금방 참조되고 말 것입니다.
iMesh의 규모가 더욱 커진다면 이 디폴트 값 역시 변경해야 할 것입니다.
10장 Conclusion(결론)
우리는 놀라운 잠재력을 가진 새로운 암호화화폐 aidos kuneen을 소개했습니다.
Aidos kuneen은 모든 트랜잭션들이 서로 작용하고 DAG(방향성 비선형 그래프) 구조를 형성하는 imesh라는 기술을 사용합니다.
우리는 이중 거래를 방지하기 위해서 DAG 구조 안에서 올바른 거래임을 증명하는 SPECTRE라는 기술을 사용합니다.
또한 우리는 양자 컴퓨터 해킹을 방지하기 위해 XMSS 라는 해시값을 기반으로한 서명체계를 사용합니다.
우리의 장점인 익명성을 위해 우리는 양자 컴퓨터 해킹을 방지하는 ‘ZKBoo (ZKB++) 영지식 증명 방법을 활용한 AKshuffle 기술을 사용합니다.
사물인터넷(IOTs) 을 위해서 우리는 coPOW라고 불리는 공동 작업 증명 방식을 채택했습니다.
CoPOW는 거래에 참여하는 모든 송금자들이 동시에 작업 증명 방식을 수행하는 것을 말합니다.
이 모든것들을 통하여 우리는 imesh상 말단 트랜잭션의 갯수들을 시뮬레이션하고, imesh가 잘 적용되고 있는지를 확인합니다.
아이도스 퀴넨의 트랜잭션 블록 사이즈에 대해서는 지속적인 연구가 필요합니다.
일반적인 트랜잭션의 블록 사이즈는 3 kbytes 인데,
AKshuffle 블록사이즈는 500 kbytes로 약 166배 정도 차이가 납니다.
우리는 앞으로도 여러가지 문제들을 해결하기 위하여 한단계 진보된 서명 방식 기술, 차세대 양자 컴퓨팅 해킹을 방지하기 위한 영지식 증명을 연구하고 발전시킬 것 입니다.
References(참고문헌)
[1] Satoshi Nakamoto, ’Bitcoin: A Peer-to-Peer Electronic Cash System’ ,2008.
[2] Crypto Forum Research Group, draft-irtf-cfrg-xmss-hash-based-signatures-10 ’XMSS:Extended Hash-Based Signatures’
,2017.
[3] Serguei Popov, ’The tangle’ ,2017.
[4] Sheldon M. Ross, ’Introduction to Probability Models. 10th Edition’ ,2012.
[5] Sergio Demian Lerner, ’DagCoin: a cryptocurrency without blocks’ ,2015.
[6] Johannes Buchmann, Erik Dahmen, Andreas Hülsing, ’XMSS — A Practical Forward Secure Signature Scheme
Based on Minimal Security Assumptions’ ,2011.
[7] Irene Giacomelli, Jesper Madsen, Claudio Orland, ’ZKBoo: Faster Zero-Knowledge for Boolean Circuits’ ,2016.
[8] Melissa Chase, David Derler, Steven Goldfeder, Claudio Orlandi, Sebastian Ramacher, Christian Rechberger, Daniel
Slamanig, Greg Zaverucha, ’Post-Quantum Zero-Knowledge and Signatures from Symmetric-Key Primitives’ ,2017.
[9] Yonatan Sompolinsky, Yoad Lewenberg, and Aviv Zohar, ’SPECTRE: Serialization of Proof-of-work Events: Confirming
Transactions via Recursive Elections’ ,2016.
[10] Peter W. Shor, ’Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum
Computer‘ ,1995.
[11] Masoud Mohseni, Peter Read, Hartmut Neven, ’Commercialize early quantum technologies‘ ,2017.
[12] PQCRYPTO, ’Post-Quantum Cryptography for Long-Term Security, Initial recommendations of long-term secure
post-quantum systems‘ ,2015.
[13] Nicolas van Saberhagen, ’CryptoNote v 2.0‘ ,2013.
부록A 시뮬레이션 결과
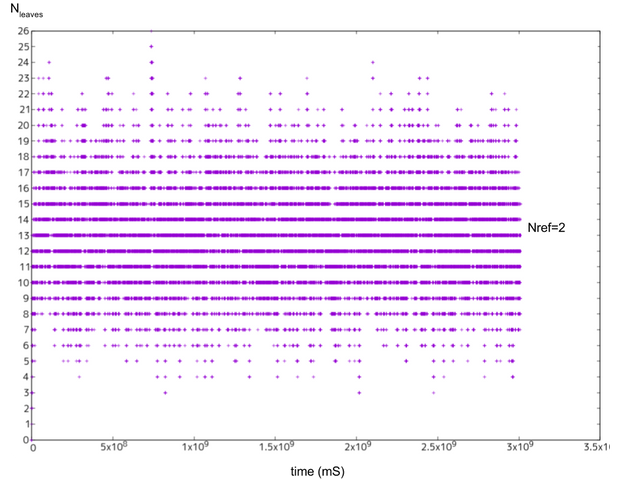
그림8: =매분 1 트랜잭션,
=2일 경우의 말단 트랜잭션 수
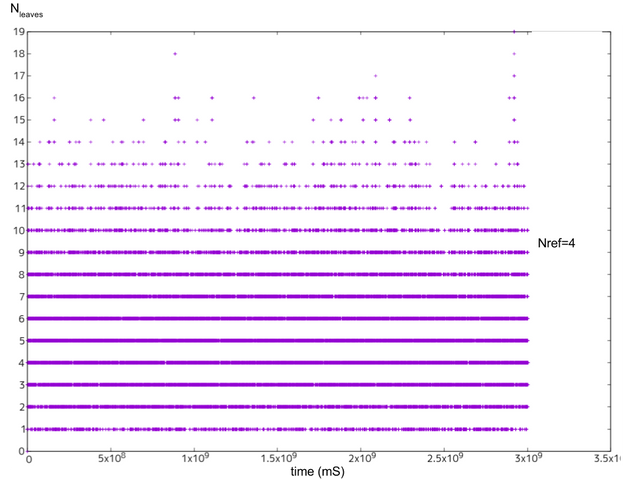
그림9: =매분 1 트랜잭션,
=4일 경우의 말단 트랜잭션 수
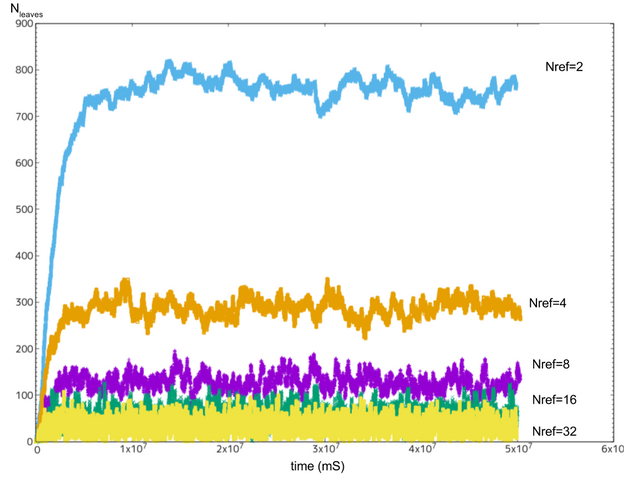
그림10: =1TPS일 경우의 말단 트랜잭션 수
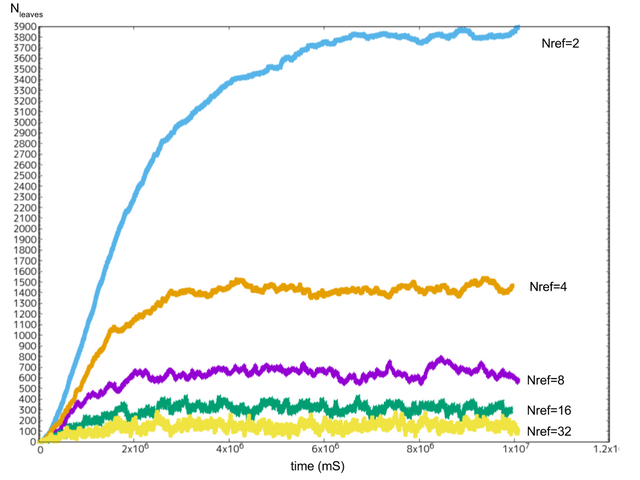
그림11: =5TPS일 경우의 말단 트랜잭션 수
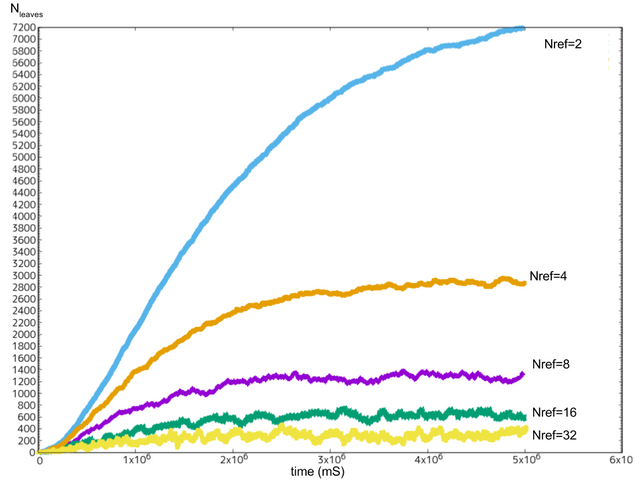
그림12: =10TPS일 경우의 말단 트랜잭션 수
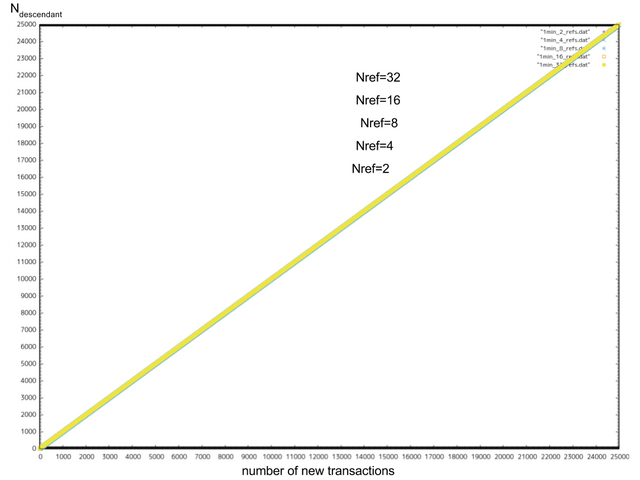
그림13: =매분 1 트랜잭션일 경우의
의 성장
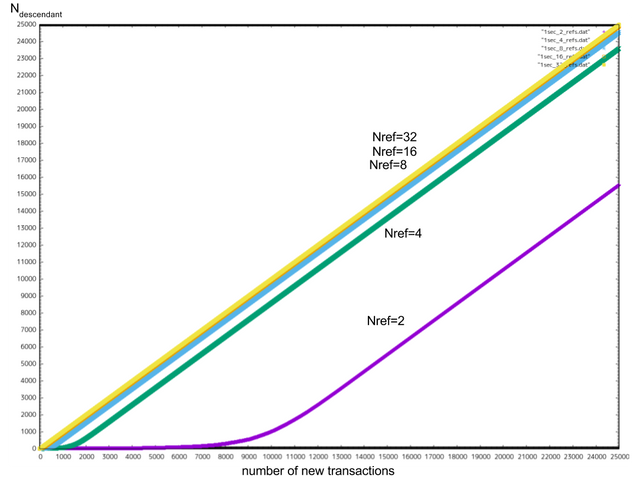
그림14: =초당 1 트랜잭션일 경우의
의 성장
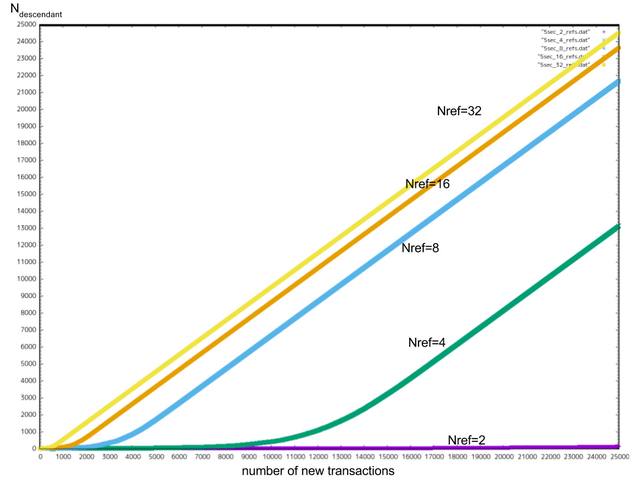
그림15: =5TPS일 경우의
의 성장
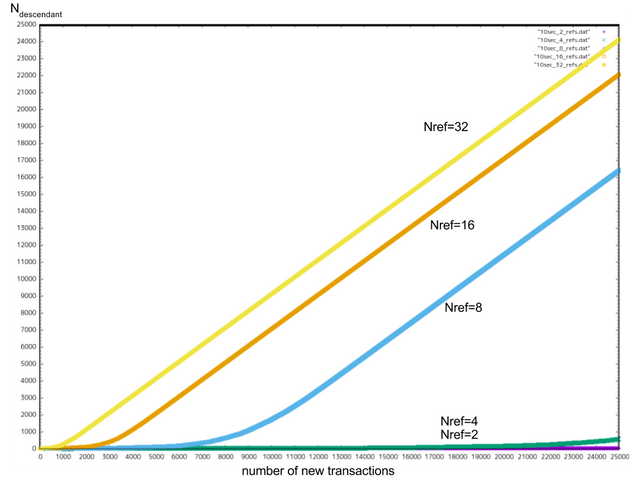
그림16: =10TPS일 경우의
의 성장
드디어 백서번역이 완료되었군요,
모두 정말 수고많으셨습니다~!!!!
드디어 나왔군요ㅎㅎADK는 이제 시작입니다.
고생 많으셨습니다ㅎㅅㅎ
출근 길에 올려주신 한글판 백서를 읽고 놀라서 영문 백서를 봤는데 번역 퀄리티가 엄청나네요.
다들 블록체인쪽에 종사하시나요?
제 기준(저의 능력이 미천하여)에서는 기술을 어느 정도는 이해해야 번역이 가능할 것 같은데. 다들 능력이 좋으시네요.
한글로 번역된 내용도 잘 이해를 못하지만 저도 관심을 가지고 공부를 많이 해야겠다는 생각이 드네요.
혹시 블록체인 쪽으로 계획중이신 번역 프로젝트 있으면 포스트 부탁드릴게요. ^^ 제가 참여할 수 있을지 모르겠지만 번역하면서 블록체인 공부도 하고 좋을 것 같습니다.
번역하시느라 다들 고생하셨습니다.