[금융투자]몬테카를로 시뮬레이션이란?(+금융에 어떻게 쓰일수 있을까?)(1)
안녕하십니까. 금융과 데이터분석을 좋아(만)하는 배성기입니다!
앞으로 금융과 데이터분석에 관한 글들을 쓸 예정입니다.
팔로우해주시면 감사합니다~
이번에 이야기 할 것은
"몬테카를로 시뮬레이션"
이란 것에 대해서 입니다.
몬테카를로(Monte-Carlo)는 도박으로 유명한 모나코의 도시이름을 따온 것입니다.
몬테카를로 시뮬레이션이란 어떠한 임의의 상황을 난수로 발생시켜
문제를 해결하는 방법론을 이야기합니다.
즉, 핵심은
"난수"
입니다.
몬테카를로를 설명하는데 가장 보편적으로 쓰이는
"난수를 사용한 원주율 추정"
을 보도록 하겠습니다.
x축과 y축을 가진 2차원 좌표상에서
중심이 (0,0)이고 길이가 2, 높이가 2인 사각형이 있습니다.
그리고 이 사각형에 내접하는 반지름이 1인 원이 있습니다.
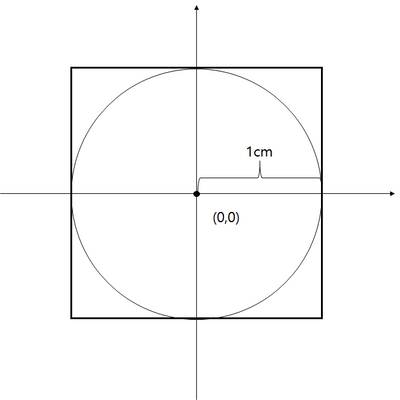
그렇다면 저 사각형안에 아무렇게나 백만개의 점을 찍으면 어떻게 될까요?
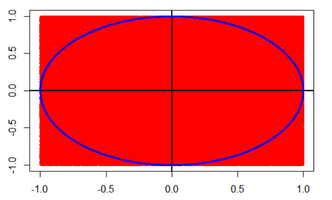
보시는 것처럼 마치 색칠을 한듯 보입니다.
아무렇게나 찍은 점 중에나 몇개의 점이 원안에 들어가있는지를 안다면,
원이 사각형의 면적에서 차지하는 비중을 알 수 있지 않을까요?
컴퓨터를 이용해서 세 본 결과
785,699개의 점이 원안에 들어가 있었습니다.
그렇다면 이것을 통해 원의 넓이를 추정할 수 있습니다.
사각형의 넓이가 4고, 원은 사각형의 넓이에서 78.57%(=785,699/1,000,000)을 차지하므로
원의 넓이는 3.14입니다.
이때 원의 넓이는 r^2 * PI 이므로, PI = 3.14를 추정할 수 있습니다.
찍은 점의 개수가 많을 수록 더 원주율에 근사한 값을 구할 수 있습니다.
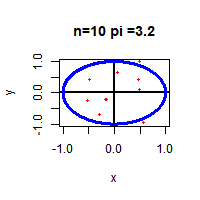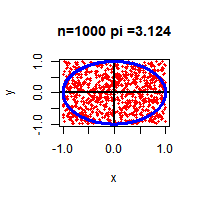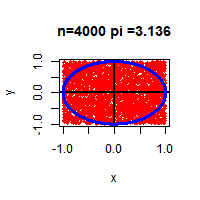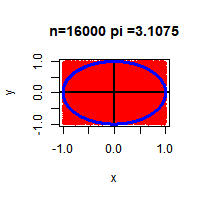
별로 궁금하실분은 없을 것 같지만 R코드도 함께 첨부합니다.
# 실습 1
# 몬테카를로 시뮬레이션을 이용한 원주율 추정
n <- 1000000
es_circle <- function(n){
data <- cbind(runif(n, min = -1, max = 1),runif(n, min = -1, max = 1))
colnames(data) <- c('x','y')
N <- length(which(data[,1]^2 + data[,2]^2 <= 1))
PI <- N/n * 4
plot(y~x,data=data, ylim = c(-1,1), xlim = c(-1,1),
pch = c(20), cex = 0.7, col = 2,
main = paste('n=',n,' pi =',PI,sep=''))
abline( v = 0, lwd = 2); abline( h = 0, lwd = 2)
theta <- seq(-pi,pi,length=1000)
x<- cos(theta); y<- sin(theta)
polygon(x,y, lwd=3, border = 4)
}
library(animation)
for (i in c(10,100,1000,2000,4000,8000,16000)) {
es_circle(i)
}
그렇다면 몬테카를로 시뮬레이션을 금융에서는 어떻게 사용할 수 있을까요?
다른 간단한 예를 보도록 하겠습니다.
금융시장으로 들어가기전에,
도박에서 생겨났다고 하니 도박에서는 어떻게 사용할 수 있을까?
간단한 예제를 통해 보도록 하겠습니다.
여기 두가지 베팅방법이 있습니다.
**첫번째는 마틴게일(Martingale)베팅입니다. **
수학적으로 배당이 2배인 게임에 최초에 1의 돈을 베팅했다고 치자. 1의 돈을 잃고나서 2의 돈을 베팅해서 따면 1의 순이익이 남는다. 만약 2를 베팅하고도 잃으면 총 손실은 3이 되는데 거기서 4를 베팅해서 따면 1의 순이익이 남는다.
이렇게 몇번을 잃었던 단 한번만 성공하면 최초 베팅금액 만큼의 돈을 따게된다. 게다가 확률이 2분의 1인 게임의 경우 한 번이라도 이길 확률은 시행 수에 따라 50%, 75%, 87.5%.... 로 100%로 수렴하게 된다. 즉 1. 재산, 즉 배팅할 수 있는 기회가 무한하고, 2. 승률*배당이 1 이상인 시행 경우의 두 가지 조건을 충족할 경우 이론상 마틴게일 배팅법은 배팅하는 사람에게 무한정 이득을 주는 시행
어떻게 보면 일종의 물타기(=자산가격이 하락하면 추가금을 투입해 평단가를 낮추는 행위)와 비슷한 전략입니다.
두번째는 켈리비율(Kelly formula)베팅입니다.
켈리비율은 일련의 반복되는 게임에서 최적의 베팅규모를 결정하는 공식으로,
지난번글에서 에드워드 소프가 사용했던 공식입니다.
공식은 아래와 같습니다.
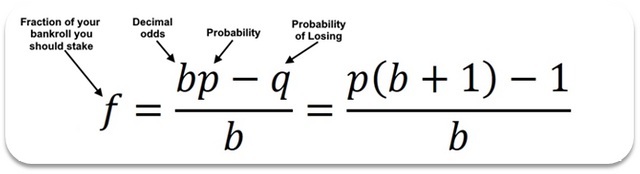
이는 유리할때 투자금을 늘리고, 불리할때 투자금을 줄이는 것으로,
일종의 피라미딩전략이라고 볼 수 있습니다.
잠깐 다른 이야기..
켈리공식을 주식시장에 적용해 본다면
주식시장이 Martingale 확률과정 이라고 가정한다면
승패율이 같으므로 p = q
주식시장에 투자할 경우 평균수익률만큼의 수익이 기대됨
단, 주식은 위험자산이므로 표준편차만큼의 손실 혹은 추가이익을 얻을 수 있음.
주식에 투자하지 않을 경우 얻을 수 있는 무위험 수익을 감안함.
그렇다면 주식시장에 투자할 최적의 투자비율은
최적 투자비율 = (기대 수익률 - 무위험 수익률) / 분산
위의 두개의 베팅전략이 주어졌을 때,
지금 자신의 상황에서는 어떤 베팅전략을 선택해야할지,
몬테카를로 시뮬레이션을 통해 해결할 수 있습니다.
가상의 난수로 승리와 패배등의 상황을 발생시키고,
해당 베팅전략으로 게임에 참여함으로써
기대 수익률을 알고 전략의 우월성을 알 수 있습니다.
내일 이어서 쓰겠습니다ㅠ.
