[수학] 단위분수 이야기 – 이항분리의 활용
안녕하세요! ryanhan입니다.
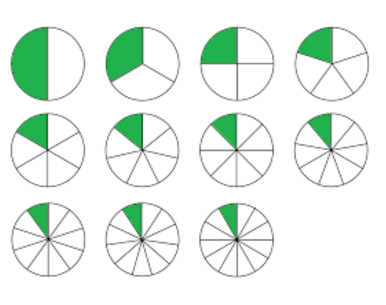
저번 포스팅에서 단위분수의 합을 이용하다가,
다음과 같은 식이 나왔다고 했습니다.
1/n = 1/(n+1) + 1/n(n+1)
이 식에서부터 ‘이항분리’라는 아이디어가 나오게 됩니다.
이항분리는 기본적으로 어떤 값을 분리하여서,
더욱 쉽게 계산하는 방법입니다.

이항분리의 뜻
이항분리는 1/n = 1/(n+1) + 1/n(n+1) 이라는 식을
1/(n(n+1))=1/n-1/(n+1)
로 바꾸면서 시작됩니다.
이 식을 이용하여 다음과 같은 값을 구할 수 있습니다.
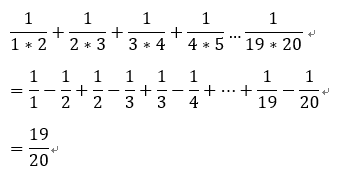
기차놀이를 하듯이, 앞의 항과 뒤의 항이 없어집니다.
일일이 1/2 + 1/6 +1/12 를 할 필요가 없는 것이죠.
이 아이디어는 어떻게 활용될 수 있을까요?
이 아이디어를 활용하기 위하여,
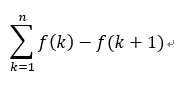
꼴로 표현되는 함수를 찾게 됩니다.

거듭제곱의 합으로 응용
가우스의 어린시절에 아주 유명한 일화가 있습니다.
1부터 100까지의 합을 구하는 방법이죠.
이 방법에서 나아가
1부터 100까지 제곱의 합,
1부터 100까지 세제곱의 합
등등을 구하는 방법을 사람들이 알아냈습니다.
이번 포스팅에서는 1부터 k까지 제곱의 합을
구하는 방법을 소개해보겠습니다.

로 나타낼 수 있습니다.
결과 적으로

오늘은 이항분리를 활용하여,
거듭제곱의 합을 구하는 방법을
소개해 보았습니다.
감사합니다.
ryanhan이었습니다.
오.. 몰랐던 부분을 알게되네요. 오래만에 가우스 일화를 떠올려 봅니다.
또 찾아주셔서 감사합니다!!^^
저도 차근차근 정리해보고 있습니다 ㅎㅎ
어질어질 어렵어렵 ^^
너무 복잡하죠.......
수식을 잘 표현하고 싶은데 방법이 없네요 ㅠㅠ
3월의 시작을 아름답게 보내세요^^
오치님 감사합니다!!
행복한 3월 되세요!
화이팅 입니다 라이언한님
응원 감사합니다!!!!!!!
저런 계산식을 본건 얼마만인지 모르겠네요.
그래도 오랜만에 보니 잼있습니다.
좋은 글 잘 보고 갑니다.
보팅 및 팔로우하고 갈게요 ^^
breezy님 감사합니다!!!
수식을 좀 보기좋게 표현했어야 하는데 ㅠㅠ..
재밌게 봐주셔서 감사해요~~~~