[번역] 비트코인 key에 쓰이는 타원 곡선 암호화에 대해 알아보자 - 2부 ( 부제 : ECC 파헤치기 )

icoreport (51)in #kr • 7 years ago (edited)

안녕하세요. ICOREPORT에 @sanghyun 입니다.

비트코인에는 여러 방법의 암호화가 사용됩니다. 그 중에서 키 값들을 암호화 시키는 방법인 타원 곡선 암호화에 대해 글을 써보도록 하겠습니다.

본 자료는 1부,2부로 나뉘어져 있으며 1부는 타원 곡선 암호화를 배우기전 워밍업 정도로 생각하시면 될것같습니다. 2부는 타원 곡선 암호화에 좀 더 초점을 맞추고 장단점에 대해 서술 해보겠습니다.

본론에 나가기에 앞서, 이 글은 블록체인에 관한 국내 자료가 매우 부족하다고 생각하여 해외 자료중 잘 정리된 글을 번역한 것임을 알려드립니다. (원서링크 : https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/ )

Elliptic curves: Building blocks of a better Trapdoor

연구자들은 RSA와 Diffie-Hellman을 도입한 후 인수 분해(factoring)을 뛰어 넘는 다른 수학을 베이스로한 암호화 솔루션을 연구했습니다. 1985년에 타원 곡선(Elliptic curve)을 베이스로 하는 암호화 알고리즘이 제안되었습니다. 그러나 타원 곡선이 정확히 무엇이고 어떻게 트랩도어 함수가 작동할 수 있을까요?

불행히도, 우리 모두가 중학교에서 처음 인수 분해를 배웠던것과는 달리 대부분의 사람들은 타원 곡선에 친숙하지 않습니다. 그래서 여기서는 몇가지 섹션을 통해 설명해보도록 하겠습니다.

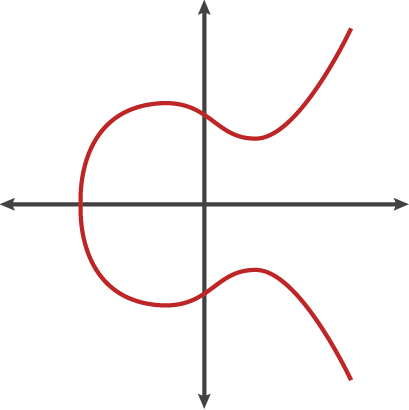
타원 곡선은 특정 수학 방정식을 만족하는 점들의 집합입니다. 식과 그래프는 다음과 같습니다.

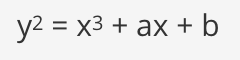
타원 곡선은 단순한 예쁜 그림이 아니며 암호 작성에 적합한 속성을 가지고 있습니다.

Strange symmetry

위에 타원 곡선을 자세히 살펴봅시다. 흥미로운 특징이 몇 가지 있는데 이들 중 하나는 수평 대칭입니다. 그리고 더 흥미로운 특징은 비 수직선(non-vertical line)이 최대 3개 지점에서 곡선을 교차한다는 것 입니다.

이 곡선을 당구 게임이라고 생각해보겠습니다.

이 당구 게임에서는 A 지점에서 공을 가져와서 B 지점으로 쏴버립니다. 그럼 비수직선이 아닌 경우라면 A와 B점이 아닌 나머지 한점과 공이 만났을때 공이 위로 또는 아래로 튀어 오릅니다. (아래그림 참조)

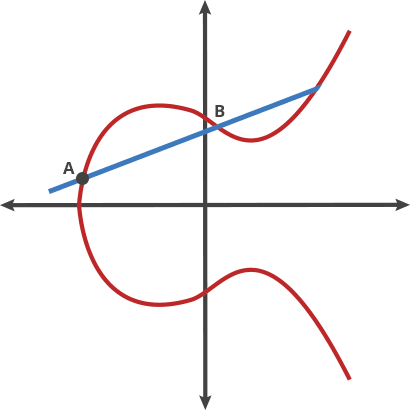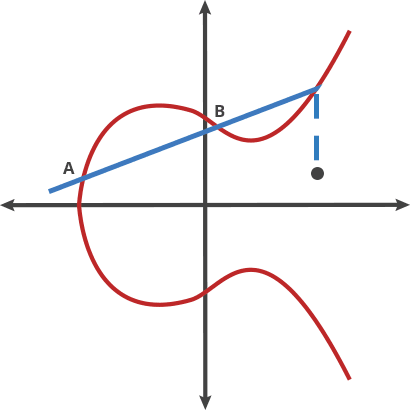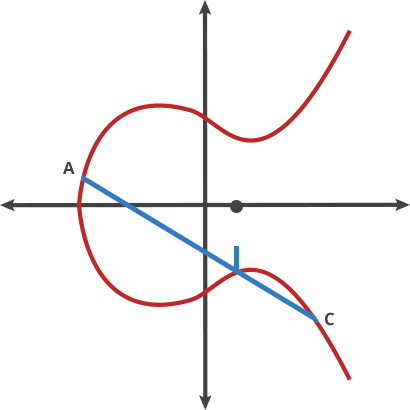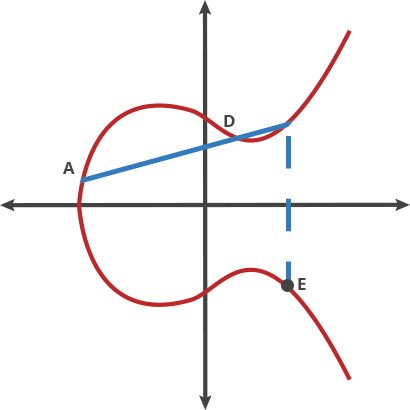
우리는 이러한 이상한 움직임을 두 점의 "dot" 이라고 부릅니다. 곡선 위의 어떠한 두점은 새로운 점을 얻기 위해 dotted 될 수 있습니다.

(위 그림과는 무관한 예시 입니다.)
A dot B = C
A dot A = B (A점에서 접선을 그리고 그 접선이 타원 곡선과 만나는 점이 B)
A dot B = C
A dot C = D
...

당신이 만약 두 점을 가지고 있고 최종점에 도착하기 위해 initial point에 임의의 n번을 dot 시켜준다면, 첫번째 점과 마지막 점만 가지고서는 n을 찾는것이 어렵습니다. (do는 쉽고 undo는 어렵다는 말이고 이것은 곧 트랩도어 함수의 핵심입니다.) 설명이 좀 난잡하니 다시 당구 얘기로 돌아가보도록 하겠습니다. 한 사람이 혼자 당구를 친다고 생각해 봅시다. 위에 설명된 규칙을 반복하여 반복해서 볼을 칠 수 있습니다. 그런데 나중에 누군가가 방 안으로 들어가서 공이 끝난 곳을 확인하면, 게임의 모든 규칙과 공이 시작된 곳을 알고 있다고 하더라도 당구 게임을 다시 시작하지 않는 공이 같은 지점에 갈때까지 공을 친 횟수를 알아낼 수 없습니다. do는 쉽고 undo는 어렵습니다. 좋은 트랩도어 함수의 표본이죠.

Let's get weird

위의 단순화된 곡선은 보기 쉽고 타원 곡선의 일반적인 개념을 설명하기에 좋지만 암호화를 위해 사용하는 곡선이 어떤 모양이 되어야 하는지에 대해서는 알 수 없습니다.

이를 위해서는 RSA와 같이 고정된 범위의 숫자로 제한해야 합니다. 타원 곡선 y^2 = x^3 + ax+ b의 공식을 계산할 때 최댓값을 구할때와 같이 숫자를 rolling over (넘김 혹은 버림) 해주는 트릭을 사용할 것입니다.

최댓값을 소수로 선택하면 타원 곡선은 소수 곡선(prime curve)이라 불리며 훌륭한 암호화 속성을 갖게 됩니다.

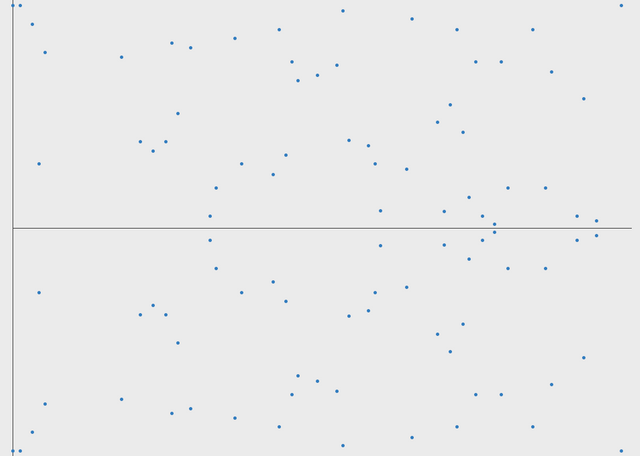
위 그림을 전통적인 시각으로 보면 곡선이라고 보기는 어렵지만 실제로 이것은 곡선입니다. 그리고 여전히 수평대칭임을 알 수 있습니다. 사실은, 당신은 여전히 이 곡선과 점을 가지고 당구게임을 할 수 있습니다. 그리고 dot 연산을 효율적으로 계산할 수 있습니다. 두 점 사이의 선을 점에 도달 할 때까지 경계에서 줄 바꿈함으로써 시각화 할 수 있습니다. 마치 당구 게임에서 볼이 보드의 가장자리에 닿았을 때, 테이블의 반대쪽으로 옮겨지는 것과 같다고 볼 수 있습니다. 그리고 그 공은 곡선위의 다른 한 점에 닿을때까지 계속됩니다. 그림을 봅시다.

이 새로운 곡선 표현을 사용하면 메시지를 가져와서 곡선에서 점으로 나타낼 수 있습니다. 메시지를 가져와서 그것을 x좌표로 설정하고, y를 풀면 곡선 위에 점을 찍는 것에 대해 생각해 볼 수 있습니다

**주의 : x값이 65인 좌표는 없으므로 현실 세계에서는 이 값을 피할 수 있습니다. **

타원 곡선 암호 시스템은 소수로서 최댓값, 곡선 방정식 및 곡선상의 공개점을 선택함으로써 정의 될 수 있습니다. 개인 키는 숫자 priv이고, 공개 키는 priv값을 priv 배수만큼 제곱하여 dotted된 공개점 입니다.물론 최댓값을 넘어갈때마다 위에 그림처럼 줄바꿈 처리를 해주겠죠? priv값을 모른다면 첫번째 점과 나중점의 위치를 알고있다고 하더라도 몇번 dot시켜주는지도 모를테니 do는 쉽고 undo는 어렵다고 할 수 있습니다. 이것은 우리가 찾고 있던 트랩도어 함수로서의 자격을 충분히 갖춘것처럼 보입니다. 이것은 우리가 찾고 있던 Trapdoor 기능으로 밝혀졌습니다.

Elliptic curves in action

최근들어 타원 곡선 기반 알고리즘이 인기를 얻고 있으며 채택 속도가 빨라지고 있습니다. 타원 곡선 암호화는 다양한 응용 프로그램에서 사용되고 있습니다. 타원 곡선 암호화는 미국 정부의 내부 통신 보호, 비트코인 소유권 증명, Apple의 iMessage 서비스의 경우 DNSCurve를 사용하여 DNS 정보를 암호화하는데도 사용됩니다. 또한 SSL / TLS를 통해 안전한 웹 브라우징 인증을 위해도 선호되는 방법입니다.

CloudFlare는 타원 곡선 암호화를 사용하여 온라인 개인 정보 보호에 완벽한 보안을 제공합니다. RSA 및 Diffie-Hellman과 같은 1세대 암호화 알고리즘은 여전히 대부분의 영역에서 표준으로 받아들여지고 있지만, 타원 곡선 암호화는 온라인 개인 정보 보호 및 보안을 위한 신속한 솔루션으로 부상하고 있습니다.

(이 글은 2013년에 쓰여서 아래에 쓸 예시가 적용이 되지 않지만 이런게 있구나 하고 이해하는 정도로 넘어가시면 좋을것 같습니다.)

최신 버전의 Chrome 또는 Firefox에서 HTTPS 버전의 이 블로그에 액세스하는 경우 브라우저는 타원 곡선 암호화를 사용하고 있습니다. 직접 확인하실 수 있습니다.

https://blog.cloudflare.com

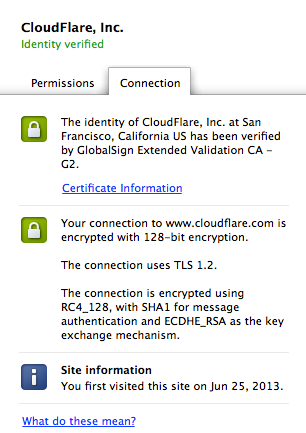
Chrome에서는 주소 표시 줄의 잠금을 클릭하고 연결 탭으로 이동하여 보안 연결을 설정하는데 사용된 암호화 알고리즘을 확인할 수 있습니다. Chrome 30에서 자물쇠를 클릭하면 다음 이미지가 보입니다.

위 사진에서 중요한 텍스트는 ECDHE_RSA 입니다. ECDHE는 Elliptic Curve Diffie Hellman Ephemeral의 약자이며 타원 곡선을 기반으로하는 키 교환 메커니즘 입니다. 이 알고리즘은 SSL내에 완벽한 전달 보안을 제공하기위해 CloudFlare로 부터 채택되었습니다. RSA 구성 요소는 RSA가 서버의 ID를 증명하는데 사용됨을 의미합니다. CloudFlare의 SSL 인증서가 RSA 키 쌍에 바인딩되어 있기 때문에 RSA를 사용합니다.

최신 브라우저는 타원 곡선 기반의 인증서도 지원합니다. CloudFlare의 SSL 인증서가 타원 곡선 인증서인 경우에 이 페이지 부분에 ECDHE_ECDSA가 표시됩니다. 서버의 신원 증명은 ECDSA (Elliptic Curve Digital Signature Algorithm)을 사용하여 수행됩니다.

CloudFlare의 ECDHE를 위한 ECC Curve

max: 115792089210356248762697446949407573530086143415290314195533631308867097853951 
curve: y² = x³ + ax + b 
a = 115792089210356248762697446949407573530086143415290314195533631308867097853948 
b = 41058363725152142129326129780047268409114441015993725554835256314039467401291

RSA가 아닌 ECDSA의 성능 향상은 극적입니다. 어셈블리 최적화 된 타원 곡선 코드가 없는 구 버전의 OpenSSL이 있더라도 256 비트 키가있는 ECDSA 서명은 2,048 비트 키가있는 RSA 서명보다 20 배 이상 빠릅니다.

맥북 프로 OpenSSL 0.9.8 (speed benchmark returns)

Doing 256 bit sign ecdsa's for 10s: 42874 256 bit ECDSA signs in 9.99s 
Doing 2048 bit private rsa's for 10s: 1864 2048 bit private RSA's in 9.99s

RSA보다 ECDSA를 사용하면 23배나 많은 서명이 가능합니다. CloudFlare는 SSL 성능을 향상시키기 위해 끊임없이 노력하고 있습니다. 이번 주 CloudFlare는 ECDHE 속도를 두 배 이상 높이는 어셈블리 최적화 버전의 ECC를 사용하기 시작했습니다. 이러한 타원 곡선 암호화를 사용하면 서버와 브라우저 모두에서 시간,전력 및 계산 리소스를 절약 할 수 있으므로 웹을 보다 빠르고 안전하게 만들 수 있습니다.

The downside

이러한 장점에도 불구하고 산업계의 모든 사람들이 타원 곡선 암호화를 사용하지 않는 몇가지 질문과 불확실성이 있었습니다. 최근 뉴스에 나온 한가지는 Dual Elliptic Curve Deterministic Random Bit Generator (Dual_EC_DRBG) 입니다. 이것은 표준 기술 연구소 (NIST)에서 표준화하고 NSA에서 홍보중인 난수 생성기 입니다.

Dual_EC_DRBG는 타원 곡선 수학을 사용하여 임의의 숫자를 생성합니다. 알고리즘 자체는 곡선에서 점을 찍고 타원 곡선 "dot" 연산을 반복적으로 수행합니다. 이 난수 생성기가 공개 된 후에 백도어로 디자인 될 수 있다고 보고가 되었는데 그 뜻은 반환되는 숫자들의 순서가 어떤 secret number를 가진 사람으로부터 완전히 예측될 수 있음을 의미합니다. 최근에 RSA라는 회사는 이 난수 생성기가 보안 제품 라인의 기본으로 설정되었기 때문에 여러 제품을 회수해야 했습니다.

(Dual_EC_DRBG 백도어에 관한 좋은 글)

https://zariski.wordpress.com/2014/01/03/%EB%82%B4%EA%B0%80-%EC%9D%B4%ED%95%B4%ED%95%9C-dual_ec_drbg-%EB%B0%B1%EB%8F%84%EC%96%B4/

이 난수 생성기가 백도어로 작성되었는지 여부에 관계없이 타원 곡선 기술 자체의 강도는 변경된 것이 없지만 타원 곡선에 대한 표준화 프로세스에 대한 질문이 제기됩니다. 이전에 말했듯이, 시스템이 적절하게 임의의 숫자를 사용하도록 하려면 주의를 기울여야 합니다.

현재 전세계의 회의론적 암호사용자들중 일부는 NIST 자체와 NSA가 지원한 출판 표준에 대해 전반적인 불신이 있습니다. 널리 구현된 타원형 곡선의 거의 모든것이 이 범주에 속합니다. Daniel Bernstein이 만든 곡선 25519와 Paulo Baretto와 공동 작업자가 최근에 계산한 곡선을 포함하여 효율적인 산술로 곡선을 개발하는 과정이 진행되었지만 이러한 곡선의 보급은 수년이 걸렸습니다. 이러한 새로운 곡선들이 브라우저에 의해 구현 될 때까지는 웹에서의 암호화 전송을 보호하는데 사용할 수 없습니다.

타원 곡선 암호화에 관한 또 다른 불확실성은 특허와 관련이 있습니다. 2009년 Certicom이 인수를 통해 BlackBerry에서 소유한 타원형 곡선의 특정 용도를 다루는 130개 이상의 특허를 가지고 있습니다. 이러한 특허 중 다수는 민간 단체 및 국가 안보국(NSA)에서도 사용이 허가 되었습니다. 이로 인해 일부 개발자는 ECC 구현이 이 특허 포트폴리오를 침해하는지 여부를 놓고 잠시 개발을 멈추었습니다. 2007년에 Certicom은 타원형 곡선의 일부 용도로 Sony에 소송을 제기했지만 2009년에는 소송이 기각되었습니다. 현재는 이러한 특허를 침해하지 않고 널리 사용되고있는 타원 곡선 암호화들이 많이 구현되어 있습니다.

ECDSA 전자 서명은 엔트로피의 좋은 소스가 필요하다는 점에서 RSA에 비해 단점이 있습니다. 적절한 임의성이 없으면 개인 키가 공개 될 수 있습니다. 안드로이드의 난수 생성기에 결함이 있어 해커가 2013년 초에 여러명의 비트코인 지갑을 보호하는데 사용되는 ECDSA의 개인 키를 찾은 사례가 있습니다. 서명을 작성하는 기계에는 난수의 좋은 소스가 필요합니다. 따라서 Dual_EC_DRBG는 권장되지 않습니다.

Looking ahead

위의 주의사항에도 불구하고 전통적인 RSA에 비해 타원 곡선 암호화의 장점이 널리 받아 들여지고 있습니다. 많은 전문가들은 RSA와 Diffie-Hellman의 수학적 알고리즘이 5년 이내에 깨질 수 있어 ECC를 유일한 대안으로 남겨두고 있습니다.

타원 곡선은 모든 최신 브라우저에서 지원되며 대부분의 인증기관에서는 타원 곡선 인증서를 제공합니다. CloudFlare 보호 사이트에 대한 모든 SSL 연결은 최신 브라우저의 ECC로 기본 설정 됩니다. 곧 CloudFlare는 고객이 자신의 타원 곡선 인증서를 업로드 할 수 있게 해줍니다. 이렇게하면 기본 메시지 보안뿐만 아니라 신원 확인에 ECC를 사용할 수 있으므로 HTTPS 세션 속도가 빨라집니다.