[doctorBME, essay] 편향(bias)과 분산(variance)의 사이에서

---

안녕하세요, @doctorbme 입니다. 오늘은 조금 편하게 적어봅니다.

기계학습(Machine Learning)을 다루다보면, 한번쯤 편향과 분산의 트레이드 오프(Bias–variance tradeoff)를 마주할 때가 있습니다. 알고리즘을 학습시킬 때, 우리가 학습시킨 알고리즘의 예측이 얼마나 정답에서 떨어져 있는지를 반영하는 편향(bias)과, 예측 자체가 얼마나 변동폭이 큰 것인지를 반영하는 분산(variance)는 서로 트레이드 오프(trade off) 관계에 있고, 이 두 개의 합이 결국 우리가 예측하는 알고리즘의 오차를 결정하는 만큼, 이 두가지 값을 적절하게 균형으로 맞추는 것이 중요하다는 것입니다.

이해를 돕기 위해 아래 그림을 살펴보도록 합시다.

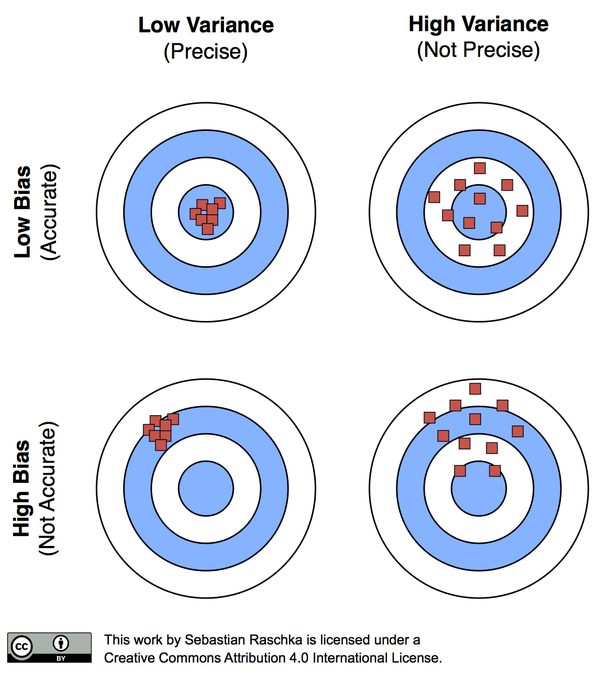
그림 1. 편향과 분산의 개념 (정확도(accuracy)와 정밀도(precision)의 개념)

왼쪽 위 그림처럼, 정확한 목표에 정확히 들어맞는다면 더할나위 없을 것입니다. 그리고 오른쪽 아래 그림처럼, 맞추려는 목표에도 어긋나고 그마저도 퍼져있다면 이 알고리즘은 실패한 것으로 볼 수 있습니다. 보통은 대체로 결과가 잘 모이기는 하는데 목표에서 빗겨있거나 (편항이 큰 상황: 왼쪽 아래 그림), 아니면 평균적으로 결과가 목표 근처에 있기는 한데, 예측을 할 때마다 퍼져있는 상황 (분산이 큰 상황: 오른쪽 위 그림)이 됩니다.

중요한 것은 이러한 편향과 분산이 트레이드 오프 관계에 있기 때문에, 어떠한 알고리즘이 학습하는 과정에 있어서 편향을 줄이려면 분산이 커지고, 분산을 줄이려면 편향이 커져, 결국 두 가지의 균형을 잘 찾아야한다는 것입니다.

예를 들어 2차원 평면에서, 두 개의 클래스를 구분하는 문제를 생각해보면, 클래스를 구분하기 위해 어떠한 경계를 설정해야할지에 따라 성능이 달라지는 것을 관찰할 수 있습니다.

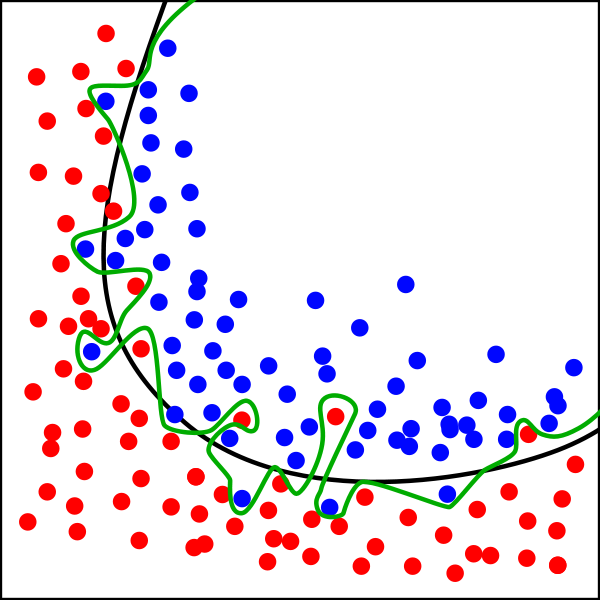
그림 2. 두 개의 클래스를 구분하기 위한, 두 가지의 경계 설정

위 그림에서, 학습데이터는 빨간 점과 파란 점으로 주어지고, 빨간 점과 파란 점의 영역을 구분하기 위해서는 검은 색을 흔히 생각할 것입니다. 뭔가 매끄러운 경계가 존재한다고 상상하는 것이 자연스럽습니다. 초록 색의 경계로 설정해도 좋기는 하겠지만, 여기에서 주어진 학습 데이터 상에서 오차가 거의 0에 가깝게 떨어지더라도, 또 다른 학습 데이터 셋(training set)이 존재해서, 이와 같은 방식으로 학습하는 경우, 학습된 모델 사이에 편차가 존재할 것입니다. 즉, 매번 학습 데이터 셋이 바뀔 때마다, 경계의 모양은 매우 구불구불할 것이고, 다시 말하자면 경계의 모양의 변화폭은 상당히 다양할 것으로 예상할 수 있습니다. 즉, 모델의 분산이 증가하는 것입니다.

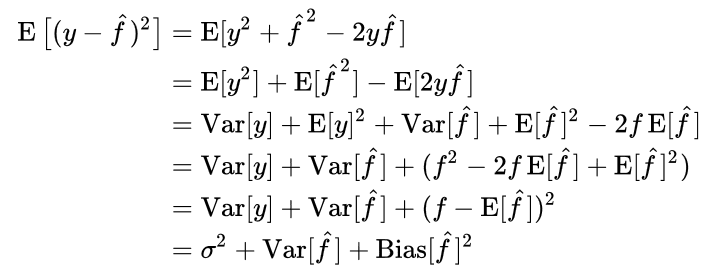
결국 전체 에러는 위와 같이 나타나는데, 첫번째 항은 우리가 절대로 줄일 수 없는 에러, 두번째는 예측 모델들 자체의 분산, 세번째는 정답 (참) 모델과 우리가 구하는 예측 모델의 기대값과의 차이인 편향을 반영합니다. 우리가 모델을 학습시키는 것은 결국 전체 에러를 가장 낮추는 방향으로 진행되기 때문에, 전체 에러가 주어질 경우, 그 사이에 편항과 분산의 트레이드 오프가 일어나게 되는 것입니다.
(여기서 주의해야할 사항 중 하나는, 학습 데이터셋 자체도 하나가 아니라, 여러 학습 데이터셋이 존재할 수 있고, 이에 대한 모델 자체의 기대 모델이 존재할 수 있다는 것입니다.)

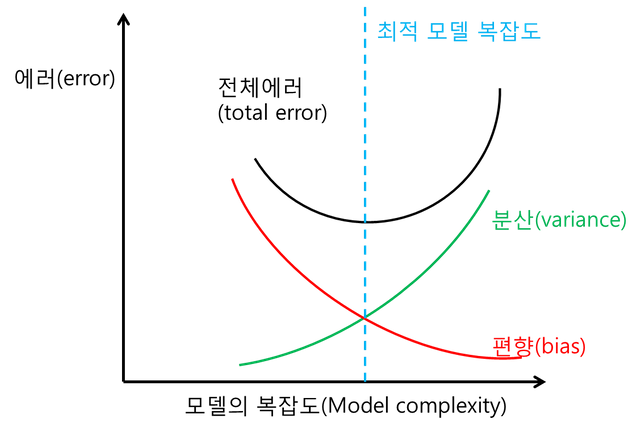
그림3. 전체 에러와 분산 및 편향의 관계

여기에서 우리는, 적절한 모델이라는 것이 결국, 분산과 편향의 균형을 고려하여 한쪽으로 치우치지 않는 최적의 복잡도를 찾는 것임을 알게 됩니다. 하지만 뒤집어서 생각해보면, 편향이 매우 작거나 분산이 매우 작은 상황이 사실은 최적의 상황이 아니라는 것도 알게 됩니다.

---

우리는 어떠한 사안에서든, 이러한 편향과 분산의 관계를 염두할 필요가 있다고 생각합니다. 어떠한 사안을 너무 단순하게 보게 된다면, 의견을 통일하기는 좋지만 사실 우리가 원하는 진실과 다소 떨어진 해답을 얻게 될 수도 있습니다. 한편 어떠한 사안을 너무 복잡하게 보게 된다면, 의견의 다양성을 반영하고 그 중심을 찾는다는 점에서는 좋지만 결국 의견이 하나로 모아지지 않을 수 있습니다. (혹은 의견을 수렴하는 데에 매우 많은 비용을 지불해야할 것입니다.) 따라서, 의견의 무조건적인 통일을 추구한다거나 의견의 매우 많은 다양성을 추구하는 것은, 결국 적절한 균형을 깨뜨리는 일이 될지도 모릅니다.

이러한 사안은 어떠한 문제에 대한 각자의 의견 수렴에 관한 이야기가 될 수도, 우리가 우리 삶을 살아나가는 방향과 경험을 위한 의사결정의 경우에도 해당이 될 수 있을 것입니다. 우리가 계속해서 편향된 결정을 하면서 산다면, 우리 삶이 주는 다양성과 다채로움을 알게되긴 힘들 것입니다. 그리고 우리가 계속해서 다양한 경험에만 집중한다면, 삶의 중심을 유지한 채 어떠한 길을 따라 앞으로 한걸음씩 나아가기 어려울지도 모릅니다. (혹은 그러기에 많은 시행착오를 겪어야할지도요.)

결국 우리가 이러한 사실에서 생각해봐야할 관점은 아래와 같습니다.

1. 어떠한 학습이든 사안이든 혹은 삶이든, 필연적으로 발생할 수 밖에 없는 고유 에러가 존재한다. 이러한 에러가 어느정도 존재할 수 있음을 인정하는 것이 필요하다.

2. 편향을 완벽히 제거하거나 분산을 완벽히 제거하는 것은 불가능하다. 그러한 방향은 오히려 우리를 위험에 빠뜨리게 될 것이다. 우리는 언제나 편향과 분산 사이에서 균형을 찾아야한다.

이것이 편향(bias)과 분산(variance)의 트레이드 오프(trade off)가 우리에게 던지는 화두일 것입니다.

---

그림 출처

그림 1, https://sebastianraschka.com/blog/2016/model-evaluation-selection-part2.html, Creative Commons 4.0 - BY
그림 2, https://en.wikipedia.org/wiki/Overfitting , Creative Commons 4.0 - BY SA
그림 3. 자체 작성