[자연과학 이야기] 박사가 사랑한 수식

안녕하세요. @yhstella 입니다.

날씨가 무더운 와중에, 반가운 비 소식이 있습니다. 서울에도 조금씩 비가 내리고 있네요.

오늘 '간단히' 써볼 이야기는 '박사가 사랑한 수식'에 대한 이야기입니다.
수식이라고 하니, 벌써 머리가 아프신건 아닌가요?^^

(출처 : www.dex.org)

'박사가 사랑한 수식'은 사실 2005년에 개봉한 영화입니다. 이 영화를 감동적으로 보았던게 벌써 12년전이네요.

(출처 : naver)

영화에 대해서는 가능하면 직접 감상을 해보시고, 관련 정보가 있는 네이버 링크만 올리겠습니다.
오늘 제가 할 이야기는 영화 내용이 아닌, 과연 박사가 사랑한 수식이 어떤 수식이고, 왜 사랑할만한지에 대한 내용이에요.
실망하셨으면 죄송합니다..ㅎㅎ





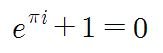
위의 수식은 '오일러의 등식' (Euler's identity) 라고 불립니다.
수학에 대해 잘 모르셔도 생긴 모양이 꽤나 간단하다는 걸 아실 수 있을 거에요.

이 수식이 어떤 수학적 의미와 조화가 있는지 아실 수 있도록 각 항목을 설명드려볼게요.

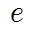
먼저 자연상수 e (Euler's number)입니다.
e는 2.71828..으로 무한히 이어지는 수인데, 다음과 같이 정의됩니다.

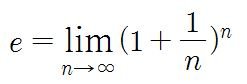
오랜만에 접하는 수식이라 어려우시다면, n을 1부터 차례대로 대입해볼게요.

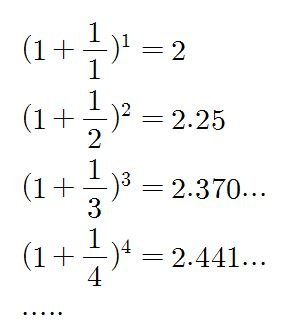
이렇게 대입하면 점점 저 e 라는 수에 가까워진다는 것입니다.
이 자연상수 e가 수학에서 갖는 의미는 매우 커서, '존 내피어'라는 수학자가 이를 발견하고 오일러가 정의한 뒤, 지수함수, 로그함수 등을 비롯한 수학의 한 분야인 '해석학' 발전의 기반이 됩니다.

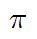
다음은 흔히들 알고 계시는 파이입니다. 파이가 어떻게 정의되는지 기억나시나요?
3.141592..이라고 알고 있는 이것은 사실 '원주율'이라고 부릅니다.

위와 같이 정의할 수 있겠죠.
원은 가장 꼭지점과 변이 없으면서도 중심을 지나는 모든 직선에 대해 대칭인 가장 아름다운 도형입니다. 이 원주율의 발견을 통해 수학의 한 분야인 '기하학'이 시작된 것은 어찌보면 당연한 일입니다.

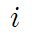
세번째는 복소수 i (imaginary unit)입니다.
현재 교과과정 상 복소수를 배우는지 안배우는지는 모르겠습니다만, 고등학교 때 배우신 분들이 꽤 있으실 겁니다.

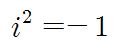
복소수 i는 정의상 제곱하면 -1이 되는 수입니다. 역사적으로는 고차방정식의 근을 구하려는 과정에서 수학자들이 발견했습니다. 즉 역시 수학의 한 분야인 '대수학'의 발전 과정에서 발견한 수입니다.

자 이제 거의 다 왔습니다.

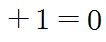
마지막은 이렇게 한 뭉테기로 써볼게요.
앞의 저 어마무시한 것에다가 1을 더하면 결과가 0이 된다는 뜻이겠죠.
그냥 앞의 것이 -1이라고 써도 될텐데, 이렇게 표현한 이유가 있습니다.

'항등원' 이라는 수학용어가 생각나시나요?

우리가 다루고 있는 자연수는 덧셈과 곱셈에 대해 '닫혀' 있습니다.
이 '닫혀있다'는 것은, 자연수에 자연수를 더해도 자연수가 나온다는 뜻입니다.
마찬가지로 자연수에 자연수를 곱해도 자연수가 나오죠.
이렇듯 '자연수'라는 집합은 덧셈과 곱셈에 대해 닫혀있다고 표현할 수 있습니다.
여기서 항등원이라는 개념이 등장합니다.
덧셈에 대한 항등원은 0 입니다. 어떤 자연수에 0을 더하면 그 자연수가 나오기 때문입니다.
곱셈에 대한 항등원은 1 입니다. 어떤 자연수에 1을 곱하면 그 자연수가 나오기 때문입니다.


설명이 길었는데, 이해하시겠나요?
즉, 0과 1은 단순해보이지만 그 수학적 의미는 각각 덧셈과 곱셈에 대한 항등원을 뜻합니다.


정리하면 다음과 같습니다.

1. 자연상수 e는 해석학의 기초가 되는 수이다.
2. 원주율 파이는 기하학의 기초가 되는 수이다.
3. 복소수 i는 대수학의 기초가 되는 수이다.
4. 숫자 0은 수 집합의 덧셈에 대한 항등원이다.
5. 숫자 1은 수 집합의 곱셈에 대한 항등원이다.

이 5개의 서로 다른 출신의 수가 모여 하나의 수식을 이루었습니다.

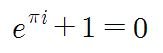
아름다움이 느껴지십니까?

오늘 말씀드리고 싶었던 것은 '수학의 아름다움' (mathematical beauty)에 대한 것입니다.
이 짧은 수식에서,
수학의 서로 다른 분야에서 온 것들이 모여 하나의 조화를 이룹니다.


저는 처음 이 수식을 알고부터, 이 영화의 박사처럼 한동안 수학의 매력에 푹 빠졌었습니다.
그리고 제가 지금껏 자연과학, 공학, 의학 등을 공부하게 된 배경이기도 합니다.

구글에 math 라고 검색해보았습니다.
복잡한 수식들만 가득한 걸 보니 수학에 대한 첫인상은 세계 어디든 비슷한가 봅니다.

아쉬웠던 점은 이 내용을 제가 정규 교과과정을 통해 배운 것은 아닌, 한 영화를 통해 배웠다는 것입니다.
쉽게 재미 붙이기 힘든 수학에 이런 매력이 있다는 것도 알리면 좋지 않을까요?
나중에 자식이 생긴다면! 저는 이런 재미를 느끼게 해주고 싶습니다. 수학말고도 많은 것들에 이런 아름다움이 숨어있을 거라고 믿습니다.


긴 글 읽어주셔서 감사합니다.
좋은 주말 밤 되세요 ^^