[고체역학] 0-2 고체역학에서 쓰이는 개념1(Hook's Law)

mechmecha (55)in #kr-science • 7 years ago (edited)

고체역학에 관해 포스팅을 해놓기로 하고 전혀 포스팅을 하지 못했습니다. 입대 때문에 주변사람들을 만나느라 신경을 쓰기도 했지만, 주요 개념들을 어떻게 기술해야하나 고민이 많았습니다.

엄밀하게 개념을 정의 내려서 서술을 할까 생각해봤지만, 그렇게 되면 가볍게 읽을 수 없는 글이 되어버릴 것 같아 최대한 간단하게 서술하기로 하였습니다.

제가 전에 고체역학은 물체가 얼마나 변형이 되는지, 얼마나 안전한지에 대해 알아보는 학문이라고 했습니다.

( [고체역학] 0-1. 고체역학(Solid Mechanics)은 무엇일까 참고)

그럼 물체의 변형 중 저희가 가장 많이 알고 있는 보편적인 예를 찾아봅시다. 바로 용수철입니다.

그림 출처

이 때 용수철에서는 훅의 법칙(Hook's law)을 만족합니다. (아마 뉴턴과 사이가 안좋았고 현미경을 이용해 처음 미시세계를 바라봤다던 그 훅입니다.)

F=-kx (F: 용수철의 복원력, k: 용수철 상수, x: 용수철의 변위)
여기서 x>0이면 용수철의 길이가 늘어나는 쪽, x<0이면 용수철의 길이가 줄어드는 쪽입니다.

이 훅의 법칙은 일반적인 막대(bar, column, beam)에서도 성립합니다. 그런데 용수철과 같이 마냥 F=kx로 정리하기엔 문제가 있습니다. 저희는 이 훅의 법칙을 좀 더 보편적으로 사용하고 싶습니다. 다시 말해서 이 훅의 법칙에서 비례 상수가 막대의 재질에 의해서만 결정되었으면 좋겠다는 뜻입니다.

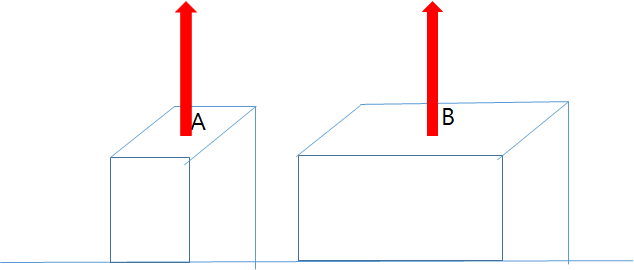
위의 그림을 봅시다. 두 막대는 똑같은 힘으로 당기고 있으며, 같은 재질로 이루어져 있습니다. 다른 점은 당겨지는 면의 표면적 뿐입니다. 저희는 직관적으로 늘어나는 변위는 단면적이 작을수록 커짐을 알 수 있습니다. ** (즉, 반비례)**

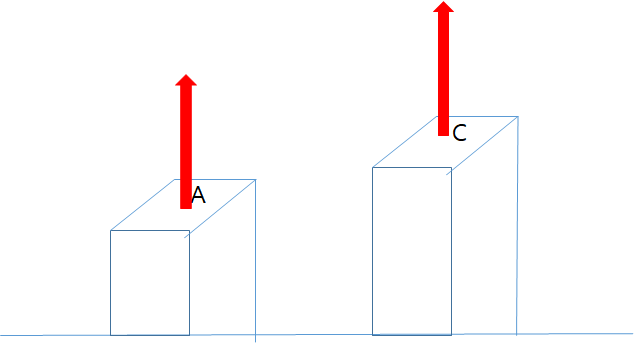
마찬가지로 위와 같이 두 막대 A,C가 있다고 합니다. 다른 점은 막대의 길이 뿐이라고 했을 때, 변위는 막대의 길이가 길어질수록 커짐을 직관적으로 알 수 있습니다. (즉, 정비례)

이 사실들을 수식으로 정리해보면 다음과 같은 식으로 나타낼 수 있습니다.

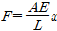여기서 F는 막대에 가한 힘, x는 변위, A는 막대의 단면적, L은 막대의 길이, E는 영 계수(Young's modulus)입니다. 여기서 영 계수는 재질(material) 마다 가지고 있는 고유한 값입니다. 이를 보면 막대도 훅의 법칙을 만족함을 알 수 있습니다.

하지만 이는 위에서도 말했듯이 보편적이지 못합니다. 그래서 여기서 새로운 개념을 도입해서 이 훅의 법칙을 영 계수(E)에 관해 표현하고 싶습니다. 이 때 응력(Stress)와 변형률(strain)이란 개념이 사용됩니다.
응력과 변형률에 대한 일단 엄밀한 정의는 다루게 되면 조금 더 까다로운(?) 수학적 개념들이 요구되므로 여기선 언급하지 않겠습니다. 그리고 앞으로 한국어 용어 대신 영어로 표기된 용어를 사용하도록 하겠습니다.

Stress의 정의는 단위면적당 작용하는 힘입니다. 단위는 Pa(N/m)로 압력과 같지만, 이는 압력과 다릅니다. 구체적으로 어떻게 다른지는 다음에 설명하도록 하겠습니다. 이렇게 정의하면 Stress(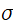)는 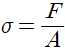로 표현됩니다. 이 때 장력(Tension)이 작용하면 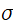는 양수, 압축력(?)(Compression)이 작용하면 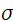는 음수값을 가집니다.

Strain의 정의는 단위길이당 변위입니다. 이렇게 정의 한다면 Strain(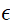)은 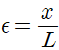로 표현됩니다. 마찬가지로 Tension이 작용하면 양수, Compression이 작용하면 음수값을 가집니다.

이 두 개념을 이용해 훅의 법칙에 관한 식 (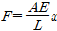)은 깔끔하게 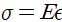로 재질에 따른 보편적인 식으로 정리됩니다.

즉, 훅의 법칙을 통해 stress와 strain의 선형적인 관계를 가짐을 알 수 있습니다. 하지만 이 훅의 법칙도 한계가 존재합니다.
stress를 주다가 strain이 비례한계(Proportional Limit) 이상으로 커져버리면 이 비례관계가 깨져버립니다.

출처

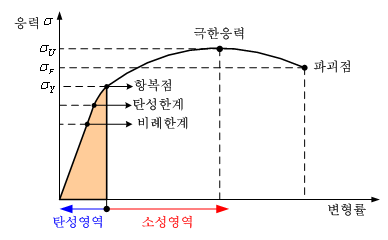
위 그래프는 stress-strain 그래프입니다. 비례한계 이후로 stress와 strain의 비례관계가 깨져버림을 확인할 수 있습니다.

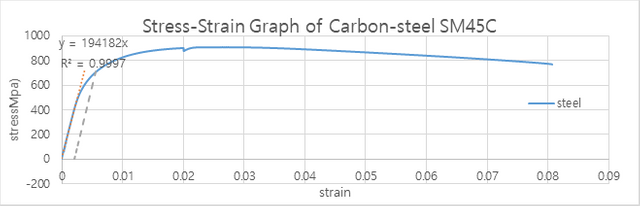
그리고 이 그래프는 학교 실험 시간에 Carbon-Steel 시료를 이용해서 구한 stress-strain 그래프입니다. 실제로도 어느 순간까지만 비례관계(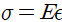)를 만족하다가 그 비례관계가 깨져버림을 확인할 수 있습니다.

다음에는 이 stress와 strain을 개념적으로 엄밀하게 파고들도록 하겠습니다. 더불어 elastic과 plastic에 관해서도 설명을 해드리도록 하겠습니다. 오늘은 고체역학의 개념을 매우매우 단순화 시켜서 설명해드렸습니다. 대충 이런 개념들을 이용하는구나 정도만 아셨으면 됐으리라 생각합니다.

#science #kr #mechanics #kr-newbie