통계유전학 (3): Testing Maker/Disease Association Through Hardy-Weinberg Disequilibrium
저는 진화생물학/집단유전학을 이해하는 것이 질병유전학에서 중요하다고 반복적으로 강조했습니다.
오늘은 Detecting Marker-Disease Association by Testing for Hardy-Weinberg Disequilibrium at a Marker Locus(1998)을 이용해 하디-베인베르크 법칙의 왜곡을 탐지함으로써 질병유전자의 위치를 특정해내는 방법을 소개합니다.
우분투로 부팅하기 귀찮아서 TeX으로 안 치고 걍 여기에 칩니다. 나중에 시간 나면 뭐 그 때 TeX으로 옮기죠.
.
우리 유전체에는 Linkage Disequilibrium이라는 현상이 있습니다. 멘델의 유전법칙 중 독립의 법칙은 두 유전자가 독립적으로 유전된다고 하지만 현실에서는 이에 위배되는 현상이 발견됩니다. 각 유전자가 독립적으로 유전되지 않고 하나의 염색체에 같이 존재하기 때문에 유전될 때 함께 전달되는 것입니다. 그러나 연관과 함께 교차도 함께 일어나기 때문에 멀리 떨어진 유전자는 같은 염색체에 있더라도 독립적으로 유전되는 것처럼 관찰되기도 합니다. 반면, 물리적으로 매우 가까운 유전자들은 상당히 오랜기간동안 교차의 영향을 받지 않고 함께 유전됩니다. 이를 Linkage Disequilibrium(이하 LD)라고 하며 두 유전좌위의 LD은 다음 식으로 측정할 수 있습니다.
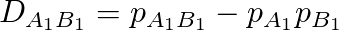
두 대립 유전자 A1과 B1이 독립적으로 유전될 경우 A1과 B1이 동시에 존재할 확률 p_A1B1의 값은 단순히 A1과 B1이 존재할 확률인 p_A1과 p_B1의 곱으로 나타납니다. 이 경우에는 D_A1B1의 값은 0입니다. 반면 A1과 B1이 함께 따라다닐 경우에는 D>0이 되고 반대의 경우에는 D<0이 될 겁니다. 아무튼 이렇게 D_A1B1은 LD를 측정하는 하나의 지표가 됩니다.
그런데 왜 LD를 측정하는 걸까요? LD는 Gene Mapping, 즉 어떤 형질(예를 들면 질병)과 연관된 DNA 서열의 위치를 특정하는데 필수적입니다. LD를 통해 좌위를 특정해내는 방법은 다음과 같습니다. 먼저 이미 위치를 알고 있는 Marker들을 유전체 상에 지정합니다. 그 다음 마커와 질병 사이의 연관을 찾습니다. 실제 질병유전자와 가까운 마커는 LD 때문에 같이 다닐 것이므로 우리는 질병과 연관이 크게 나타나는 마커 근처에 우리가 찾는 진짜배기 질병 유전자가 있을 거라고 추측할 수 있습니다.
자연스럽게 관건은 LD를 이용한 방법의 해상도가 어느정도인가? 하는 것일 겁니다. 막연하게 생각하면 마커를 짧은 간격을 두고 마구마구 늘리면 되겠지만 여러가지 이유로 이 방법에는 한계가 있습니다. 막말로 무작정 늘릴 수 있었으면 염기 하나마다 마커를 박아버리면 되겠습니다만.... 딱 봐도 매우 비효율적입니다(+다중비교문제).
더불어 우리는 D_A1B1을 직접적으로 측정하지 않습니다. 왜냐하면 D_A1B1 자체는 직접적으로 검정할만한 Test-Statistic이 없기 때문입니다. 물론 요즘은 시대가 좋아져서(물론 저는 그 이전 세대는 경험해보지 못한 인간이지만 ㅎㅎ) MC Simulation을 돌리면 test-statistic 없이도 p-value를 계산할 수 있습니다. 제 RX480은 코어가 2304갭니다. 가즈아ㅏㅏ
근데 1998은 그런 시대가 아니었습니다. 사실 지금도 되도록이면 test-statistic이 있는 방법을 선호합니다. 그게 계산량에서 싸게 먹히니까요. 데이터가 커지면 그래픽카드로 돌려도 MC는 오래 걸려서 ㅡㅡ.
그래서 LD를 바로 알아내는 방법으로 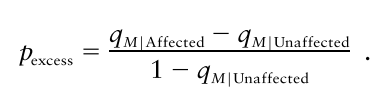 을 씁니다.
을 씁니다.
case(affected)와 control(unaffected)에서의 빈도 차이가 질병-마커 상관관계를 암시한다고 보는 것입니다. 질병 allele A가 실제 질병에 영향을 줄 경우 case와 control에서의 빈도가 다를테니까요.
얘는 다음과 같은 카이제곱 분포를 따릅니다.
p_excess와 Marker(M), Disease Susceptibility Allele(A) 사이의 관계는 계산을 통해 다음과 같음을 알 수 있습니다.
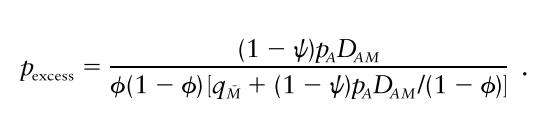
다 집어치우고 핵심만 요약하면 p_excess는 D_AM에 정비례합니다(증명은 그냥 단순 산수라서).
그리고 오늘의 주인공인 하디-베인베르크 법칙을 이용한 F_M는 성질이 좀 더 좋아서 D_AM의 제곱에 비례합니다.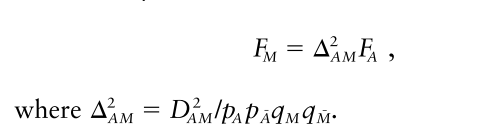
얘도 카이제곱 검정으로 확인할 수 있습니다.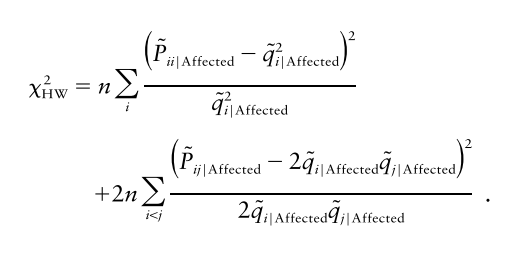
p_excess는 D_AM에 정비례하지만, F_M은 D_AM의 제곱에 비례합니다. 그말인즉슨, 마커 M이 실제 질병과 연관이 있는 allele A에 멀수록 F_M의 값이 p_excess에 비해 빨리 감소한다는 뜻입니다. 훨씬 더 좋은 해상도를 얻을 수 있다는 말이죠.
이후 논문의 시뮬레이션이 보여주는 결과는 이러한 이론적 예측이 맞았음을 보여주고 있습니다.
이렇듯 집단유전학을 알면 질병을 이해할 수 있는 도구를 더 많이 얻을 수 있습니다. 질병이 아닌 다른 형질들도 마찬가지죠. 어떻게 입만 잘 놀리면 되던 1920년 이전의 진화론이 1920년대 이후의 진화생물학과 구분되는 것은 바로 이러한 수학적 기술의 힘 덕분이었습니다. 그리고 이러한 '엄밀한' 방법론 덕분에 우리는 실제 현상을 더 구체적으로 잘 이해할 수 있게 됐습니다. 그리고 이제는 실제 질병문제를 해결하려는 단계까지 왔죠.
그렇기 때문에 저는 진화생물학을 논함에 있어서 수학과 통계학 없이 입으로만 때우는 사람들을 경계합니다. 진화생물학의 수학적 기반이 여기까지 왔음에도 그 사람들이 입으로만 때우는 건 아마 본인들의 주장이 불확실하거나 아예 틀려서 수학적으로 입증될 수 없기 때문이겠죠.
Reference
(1) Detecting Marker-Disease Association by Testing for Hardy-Weinberg Disequilibrium at a Marker Locus (http://www.cell.com/ajhg/fulltext/S0002-9297(07)61584-5)
Congratulations @hanbin973! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP분야는 다르지만, 비슷한 방법론을 이용하시는 것 같아요.
개인적으로, MCS가 비효율적일때 importance sampling으로 접근하면 꽤 경제적이고 효과적인거 같아요!