Fibonacci e la SUCCESSIONE AUREA | Fibonacci and the GOLDEN RATIO | [ITA/ENG]

Buongiorno a tutti.
Ultimamente mi sono appassionato al mondo del trading. Ho imparato ad utilizzare alcuni degli indicatori e degli strumenti più famosi, fra i quali anche gli strumenti di Fibonacci.
La mia attenzione è stata immediatamente catturata da questo nome, il quale mi ricordava immediatamente una delle leggi matematiche più ricorrenti in natura, che avevo precedentemente studiato a scuola.
Con questo articolo vorrei parlare di Fibonacci e della sua scoperta in ambito matematico.
Good morning everyone. Lately I am passionate about the world of trading. I learned to use some of the Fibonacci indicators and tools. My attention was immediately captured by this name, which immediately seemed to me one of the most recurring mathematical subjects in nature, which I had previously studied at school. With this article I would like to talk about Fibonacci and its discovery in the mathematical field.

BIOGRAFIA:
Leonardo Pisano nasce nel settembre del 1175 a Pisa.
Passa l'infanzia col padre mercante in Calibia, regione dell'attuale Algeria, dove apprende i procedimenti aritmetici che i musulmani stavano allora diffondendo nel mondo arabo, ma che in occidente erano ancora sconosciuti. Alcuni di questi procedimenti erano stati introdotti per la prima volta dagli indiani, portatori di una cultura molto diversa da quella mediterranea. Per perfezionare queste conoscenze Fibonacci viaggiò molto, giungendo a Costantinopoli.
Qui amplia le proprie conoscenze grazie a Muhammad ibn Musa al Khwarizmi, Abu Kamil e ai maestri arabi.
Ritornato in Italia, la sua notorietà giunge anche alla corte di Federico II, l'imperatore.
BIOGRAPHY:
Leonardo Pisano was born in September 1175 in Pisa, Italy.
He spent his childhood with his merchant father in Calibia, a region of present-day Algeria, where he learned the arithmetic procedures that the Muslims were then spreading in the Arab world, but which were still unknown in Europe. Some of these procedures had been introduced for the first time by the Indians, bearers of a culture very different from the Mediterranean one.
To improve this knowledge Fibonacci traveled a lot, arriving in Constantinople. Here he expands his knowledge thanks to Muhammad ibn Musa al Khwarizmi, Abu Kamil and the Arab masters. Returning to Italy, his notoriety also reaches the court of Federico II, the emperor.

ORIGINI DELLA SUCCESSIONE DI FIBONACCI:
Il volere di Fibonacci è quello di trovare una legge matematica capace di calcolare il proliferare di una popolazione di conigli.
Si pone allora delle ipotesi:
- Vi è una coppia di conigli appena nati;
- Al termine del primo mese, la prima coppia di conigli diventa fertile, generando una nuova coppia al termine del secondo mese;
- Al terzo mese vi saranno 2+1=3 coppie di conigli;
- Al quarto mese vi saranno 3+2=5 coppie di conigli, e così via;
E questo è ciò che si verifica:
- Dopo il primo mese vi sarà una coppia di conigli fertile;
- Dopo due mesi ci saranno due coppie, di cui una sola fertile;
- Al terzo mese ci saranno 2+1=3 coppie poiché solo la prima coppia fertile avrà generato; di queste tre due saranno le coppie fertili;
- Al quarto mese ci saranno 3+2=5 coppie
ORIGINS OF THE SUCCESSION OF FIBONACCI:
Fibonacci wants to find a mathematical law able to calculate the proliferation of a population of rabbits.
It then poses hypotheses:
- There is a pair of newborn rabbits;
- At the end of the first month, the first pair of rabbits becomes fertile, generating a new pair at the end of the second month;
- In the third month there will be 2 + 1 = 3 pairs of rabbits;
- In the fourth month there will be 3 + 2 = 5 pairs of rabbits, and so on;
And this is what occurs:
- After the first month there will be a fertile couple of rabbits;
- After two months there will be two couples, of which only one is fertile;
- In the third month there will be 2 + 1 = 3 pairs because only the fertile couple will have generated; of these three two will be fertile couples;
- In the fourth month there will be 3 + 2 = 5
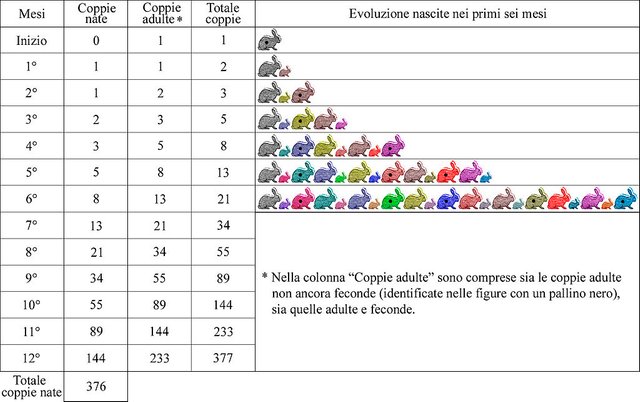
Allora Fibonacci osserva che ogni termine corrisponde alla somma dei due precedenti, e quindi:
1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Then Fibonacci observes that each term corresponds to the sum of the two previous ones, and therefore: 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

LA SUCCESSIONE AUREA NELLA NATURA:
Spirali
Come già detto all'inizio, non è difficile trovare in natura degli elementi aurei.
Uno di questi è la spirale, chiamata anche spirale aurea o logaritmica. Questa è una figura geometrica ottenuta considerando la traiettoria di un punto che si muove di moto uniformemente accelerato su una semiretta, la quale ruota uniformemente intorno alla sua origine.
Ecco di seguito un'immagine rappresentativa della spirale aurea.
AUREA SUCCESSION IN NATURE:
As already mentioned at the beginning, it is not difficult to find golden elements in nature.
One of these is the spiral, also called a golden or logarithmic spiral. The latter is a geometric figure obtained by considering the trajectory of a point that moves with uniformly accelerated motion on a half-line, which rotates uniformly around its origin.
Here is a representative image of the Fibonacci's spiral.
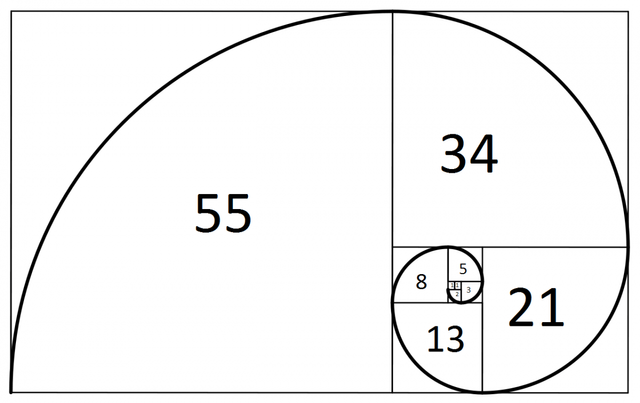
Considerando i quarti di circonferenza, possiamo notare che i rispettivi raggi corrispondono alla somma dei raggi dei due quarti di circonferenza precedenti, in ordine di grandezza.
Di seguito riporto altri esempi di successione aurea.
Considering the quarter-circumference, we can see that the respective spokes correspond to the sum of the rays of the previous two quarter-circumference. Below are other examples of succession.

Pigna: i semi si ordinano secondo spirali.
The seeds are ordered according to the spirals.

Girasole, Sunflower

Conchiglia di Nautilus, Nautilus Shell

Cavalluccio Marino, Seehorse
FIBONACCI NEL TRADING:
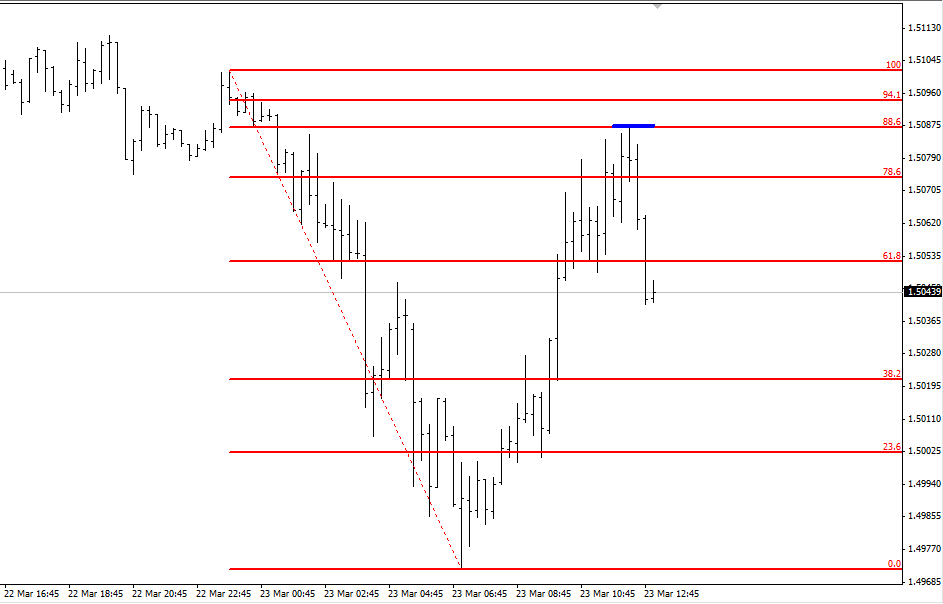
Molti trader utilizzano tale schema per impostare le frequenze degli oscillatori, così come l’ampiezza delle medie mobili.
I ritracciamenti di Fibonacci consistono in 9 livelli orizzontali dello 0%, 23.6%, 38.2%, 61.8%, 78.6%, 88.6%, 94.1%, 100% (fin qui considerati normali ritracciamenti), 161.8%, 261.8%, 423.6% (considerati estensioni).
FIBONACCI IN TRADING:
Many traders use this scheme to set oscillator frequencies, as well as the amplitude of moving averages.
Fibonacci retracements consist of 9 horizontal levels of 0%, 23.6%, 38.2%, 61.8%, 78.6%, 88.6%, 94.1%, 100% (so far considered normal retracements), 161.8%, 261.8%, 423.6% ( considered extensions).
CONCLUSIONE:
La matematica è costantemente intorno a noi, che lo vogliamo o no. E questa non è una condanna, anche se quando andavi a scuola non l'apprezzavi.
La matematica da grandi opportunità a chi le sa cogliere, e ci permette di guardarci attorno con un punto di vista diverso, con un punto di vista più interessante.
Prima di salutarvi, vi riporto un ultimo esempio di quanto la natura sia incredibile e condizionata dalla matematica:
CONCLUSIONS:
Mathematics is constantly around us. And this is not a condemnation, even if you did not appreciate it when you were attending the school.
Mathematics gives the opportunity to watch to things with another interesting point of view.
Before saying goodbye, I am going to give you one last example of how nature is incredibly conditioned by mathematics:

Riconoscete qualcosa di familiare? Esatto, quelle che si ripetono sono spirali auree.
La Via Lattea stessa è fatta così.
Vi auguro una buona giornata e vi invito a condividere nei commenti le vostre opinioni.
Do you recognize something familiar? Exactly, those that are repeated are Fibonacci spirals.
I wish you a good day and I invite you to comment below with your opinions.

Gran bel post complimenti. Avrei voluto commentare ulteriormente ma non riesco adesso.
Grazie @serialfiller, sono felice ti sia piaciuto!
Complimenti il tuo articolo è molto interessante e ben dettagliato.
@s3rj0 Grazie!
Articolo molto interessante!!!
Grazie @marcuz
We recommended this post here.
Ottimo articolo
Grazie @dubbio!