SLC S23 Week1 || Geometry with GeoGebra: Points, Lines, and Angles

We have a new season of Steemit Learning Challenge, you can check more details here Steemit Update [February 17th, 2025] : Steemit Learning Challenge Season 23 - Week 1.

I am starting this new season with @sergeyk's Geometry class, you can take a peek at it here SLC S23 Week1 || Geometry with GeoGebra: Points, Lines, and Angles and maybe you'd give it a try.

_{Thumbnail taken from Pixabay}

Now let's move to geometry.

• What is geometry? When and why did it appear? How did you study geometry in school? Were you familiar with any geometry software?

---

• What is geometry?

Geometry is a part of Math that studies shapes, sizes, and the relationships between points, lines, angles, surfaces, and solids. It is one of the oldest areas of mathematics. The Geometry word comes from "geo" which means earth and "metron" meaning measure.

• When and why did it appear?

Geometry was created as a need to measure land and building structures also for celestial movements. Later on over the years it developed more complex and abstract relations and concepts.

• Were you familiar with any geometry software?

I would not call it familiar because I didn't work with the software, in school or university I think we had the Mat Lab software presented but we didn't go further with development in the app.

• Explain different geometric primitives (point, line, angle, segment, ray) and illustrate them in GeoGebra.

---

POINT

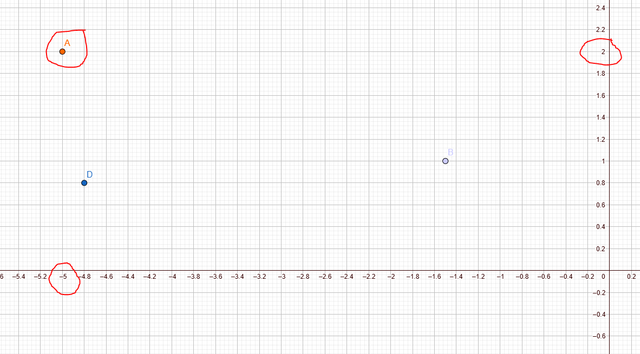
A point is a location in space that doesn't have size, width, length or depth. And as the name suggests it is represented using a dot.

In the above example you can see 4 points, A, B, C, D, each one is represented on x-y axis by two coordinates. Example for A:

A(-5;2) - (-5 on X axis, 2 on Y axis, the point is at the intersection of those 2 coordinates)

LINE & SEGMENT

Let's cover Line and Segment here:

A line is a straight path that extends on both sides infinitely (in both directions), no matter how far you zoom out you won't see the end of the line, it has no endpoints, we can say it has an undefined length.

Let's see an example:

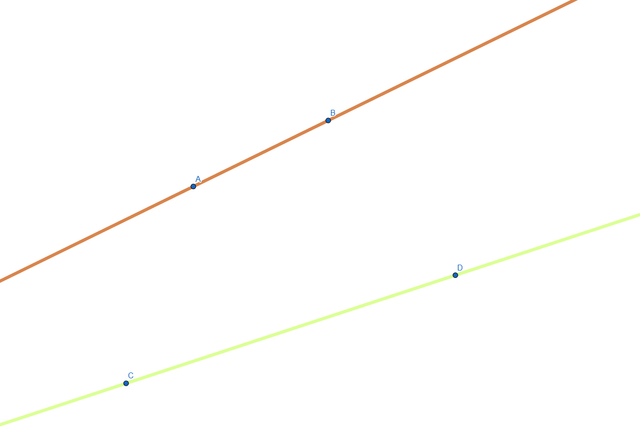
A segment is a line with endpoints, it doesn't expand infinitely, we can say it has a defined length, it stops at it's endpoints, example segment A-B below.

RAY

Ray is similar to a line but it has one endpoint, so basically it can extend infinitely only on one side the other being blocked with an endpoint.

Example:

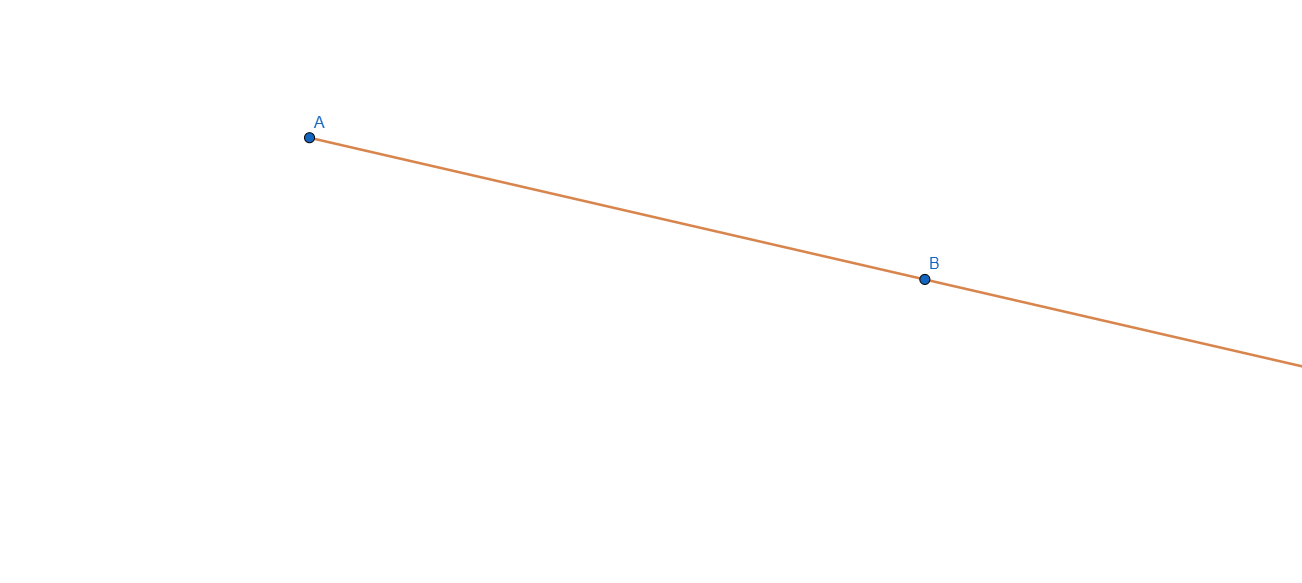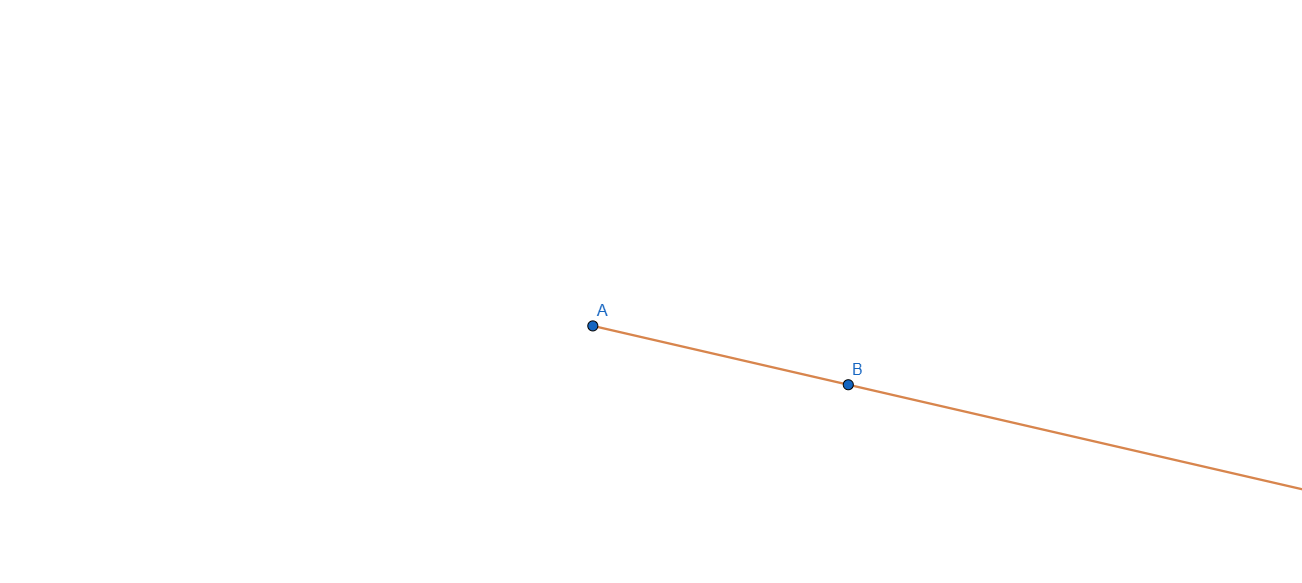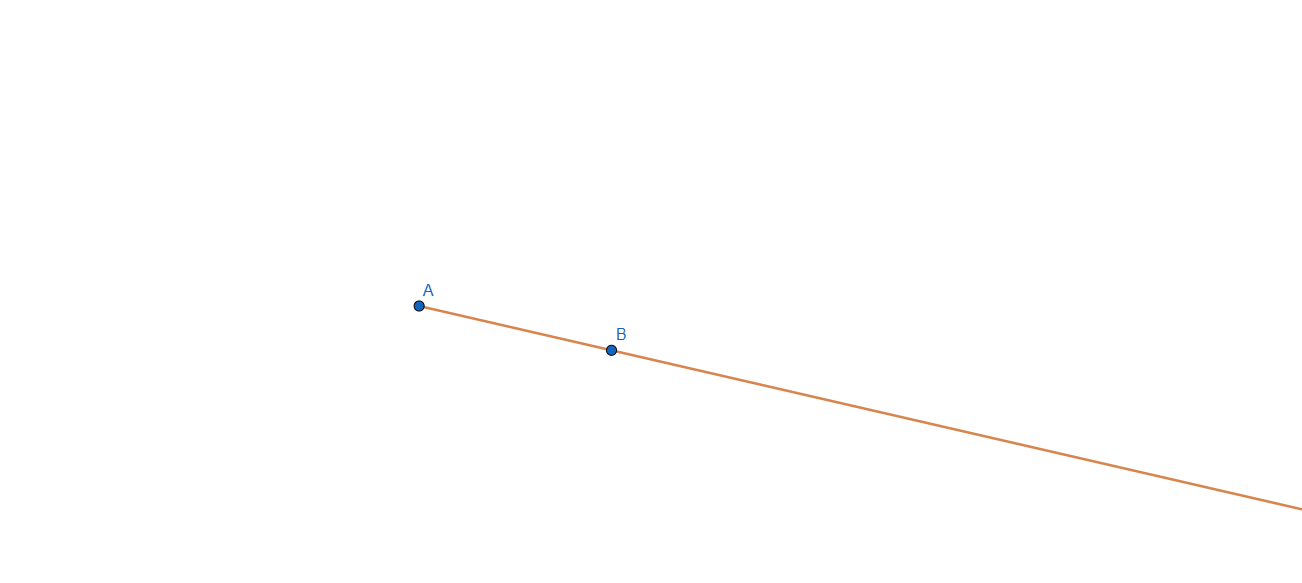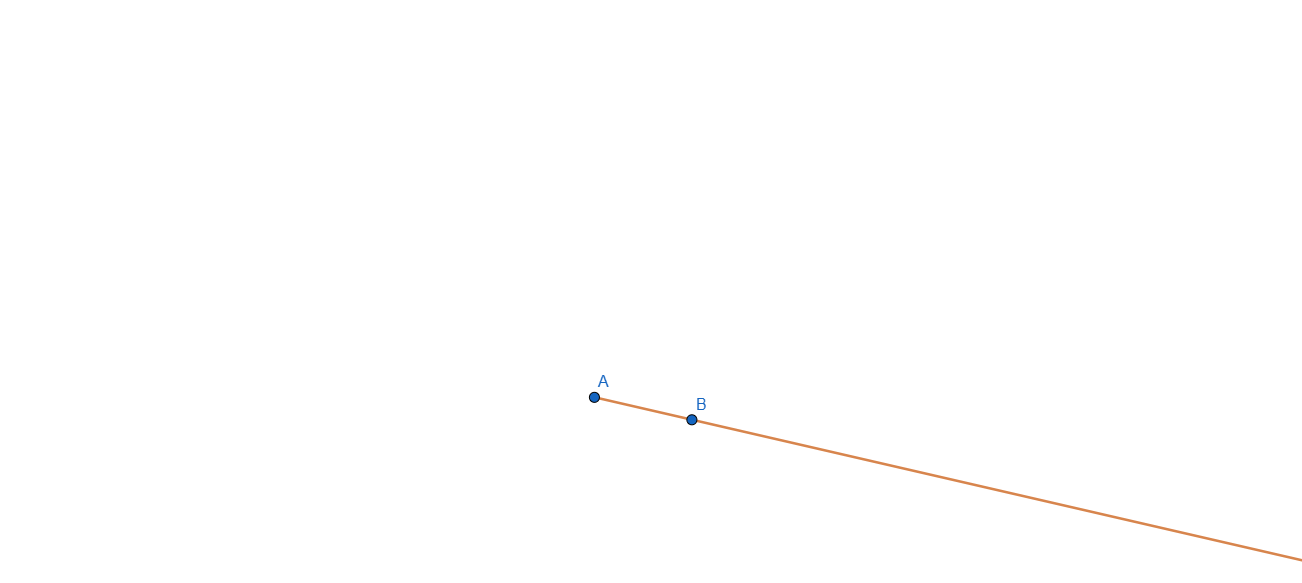
ANGLE

An angle is formed by two rays that start from a common point and the gap created by these two is called an Angle. Angles are measured in degree and show the amount of rotation between the two rays that creates it.

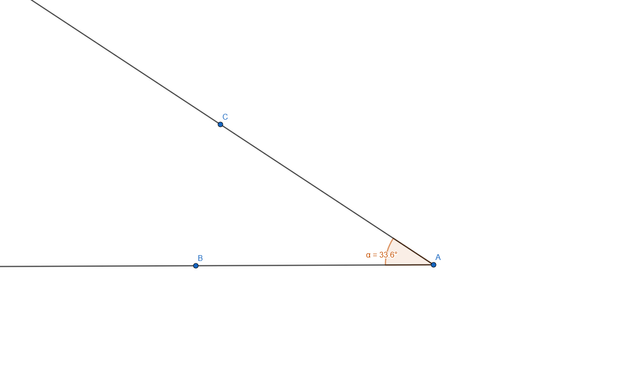
• Construct an arbitrary angle, then extend one side to create a supplementary ray—show that the sum of adjacent angles is always 180 degrees.

• Construct an angle with two supplementary rays—show that the resulting vertical angles are always equal.

---

Let's start with the two rays and the angle we need:

Now we need to measure the angles using the Angle tool. Using the Angle Tool we measure the Angles <BCD and <DCA like this:

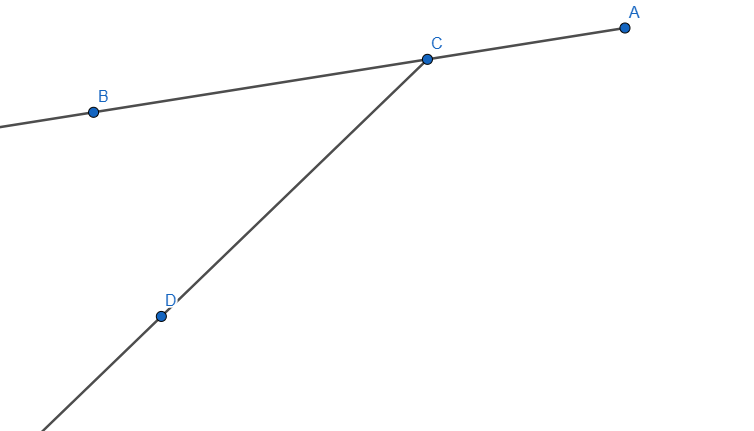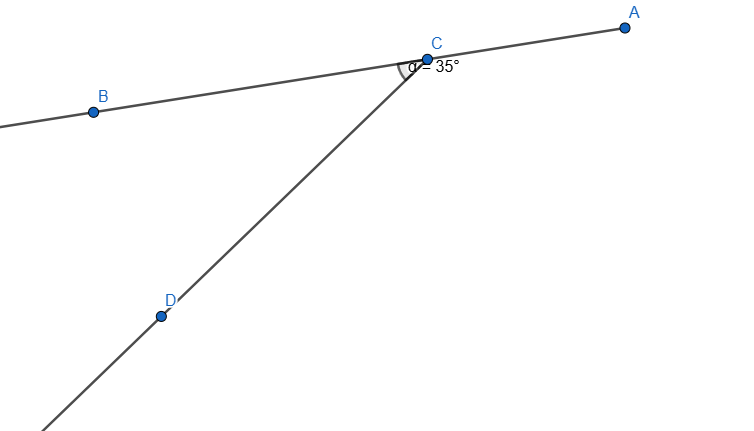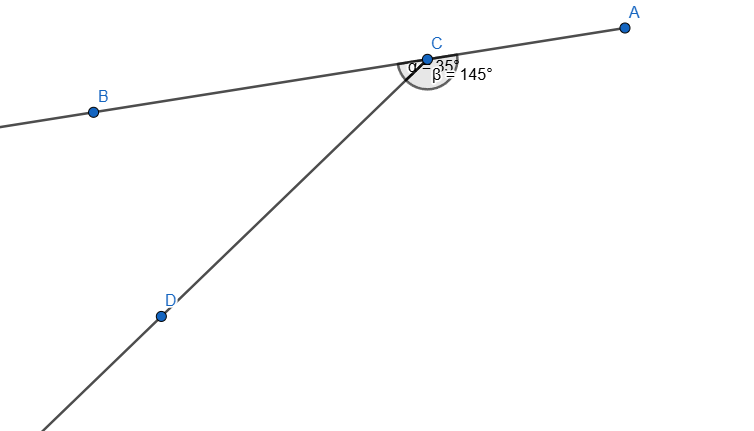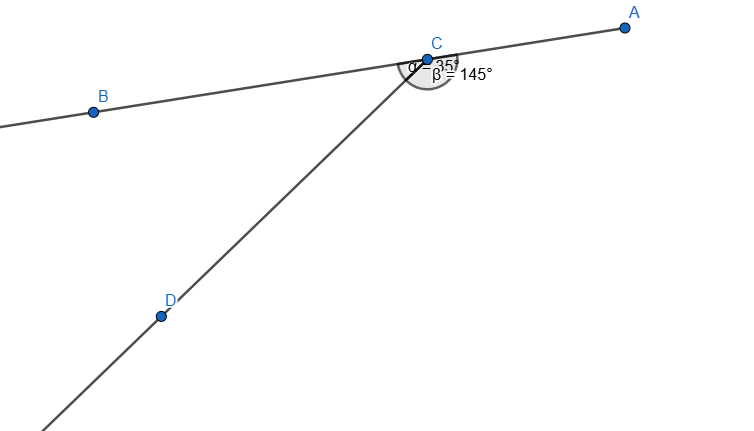
I also added some style to them so we can distinguish them easier, now let's move one of the ray and we'll see the two angles changing their value, if we add the two values the result will always be 180 degrees.

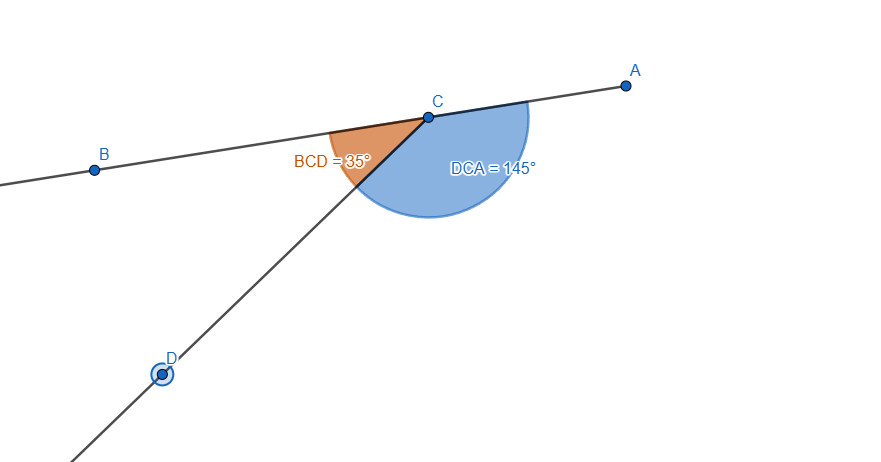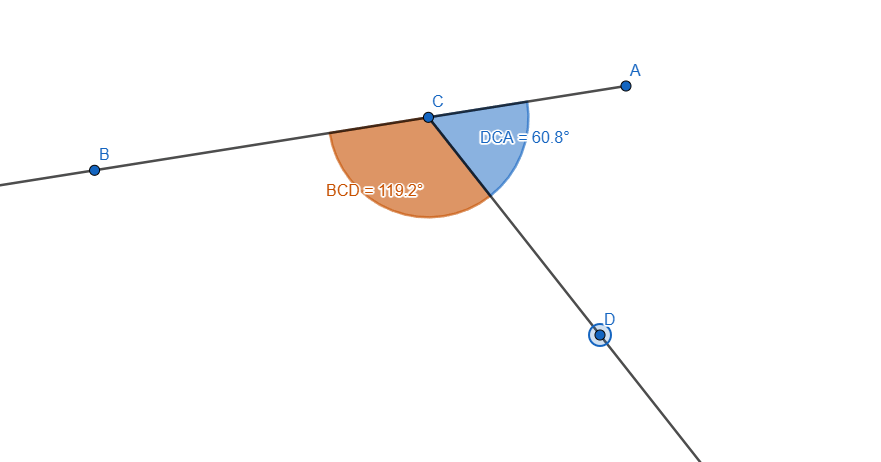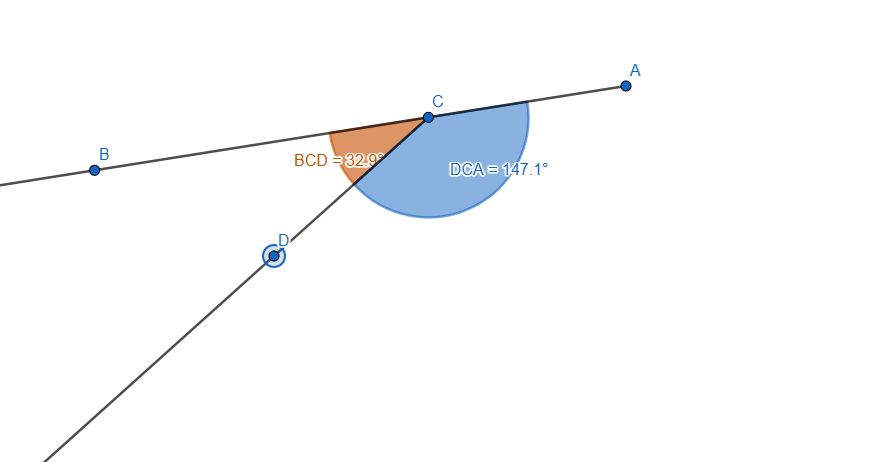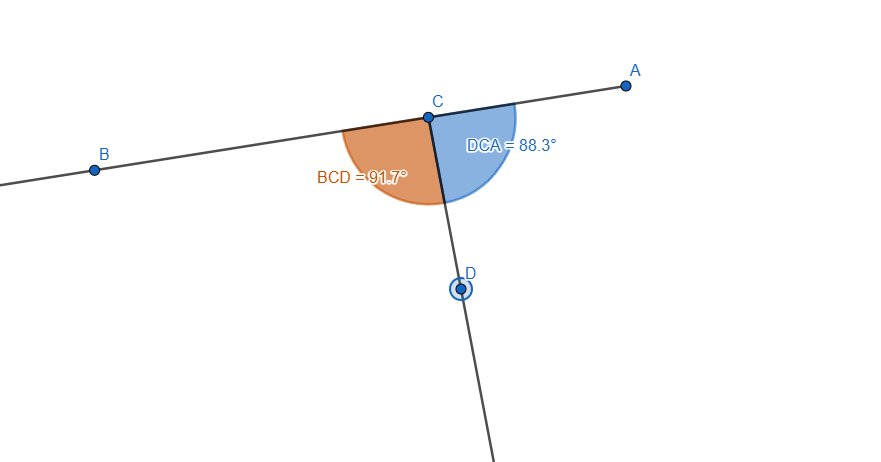
Here is a live preview, you can see we are moving one of the rays and the value of the two angles are changing. In any position we'd stop, the sum of the angles would be 180 degrees.

Now for the second part of the task:

Construct an angle with two supplementary rays—show that the resulting vertical angles are always equal.

So from what I understand in the task we need to create an intersection of two rays and prove that the opposed angles have the same value, to do that we need to start with the rays first:

With the rays added we'll have to add a point at the intersection of the rays so we can measure the angles after:

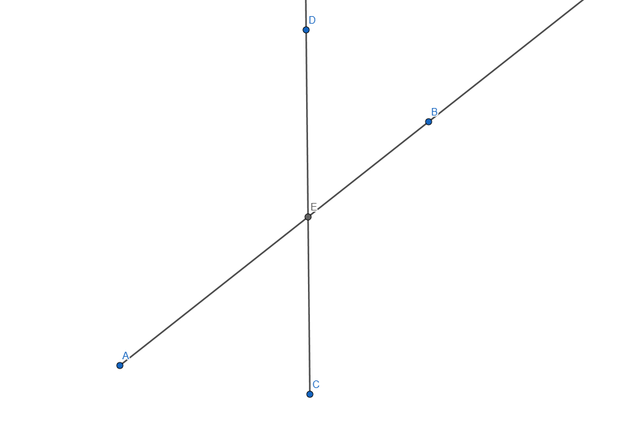
Now let's measure the angles:

• <AEC
• <DEB
• <DEA
• <BEC

as it follows:

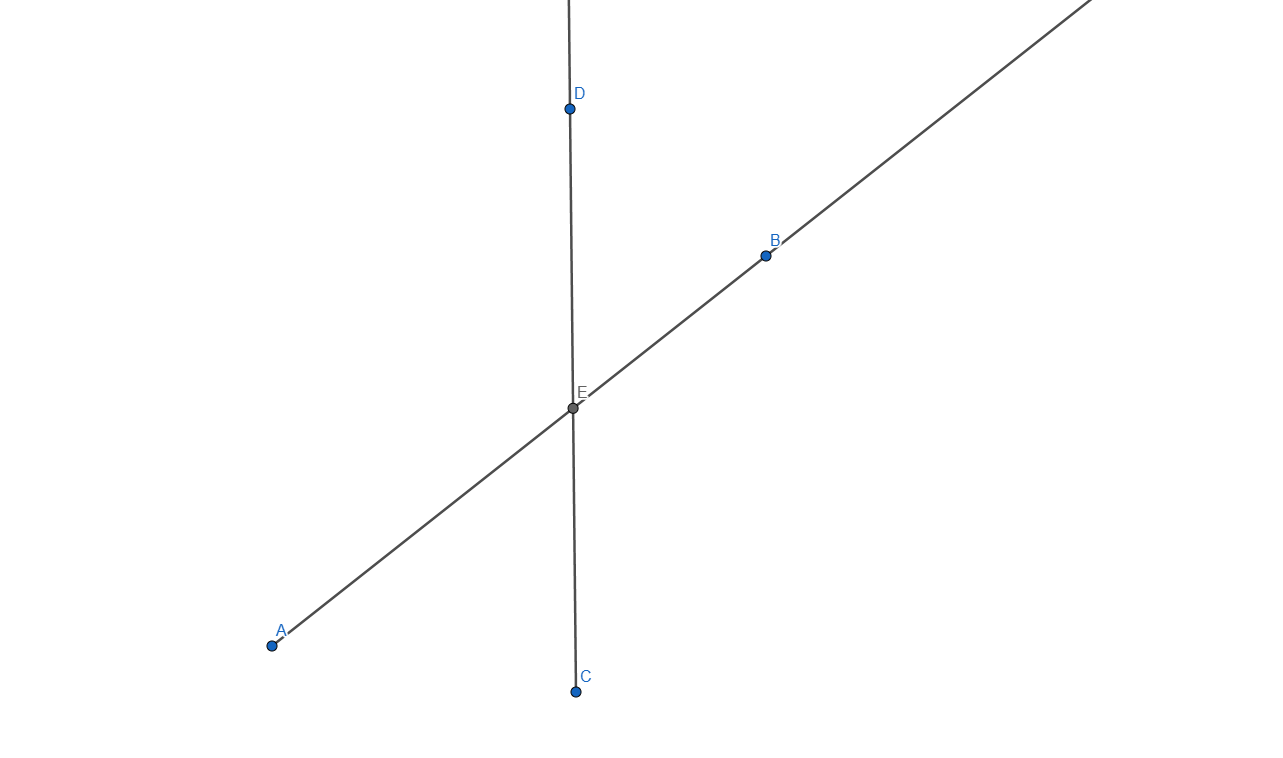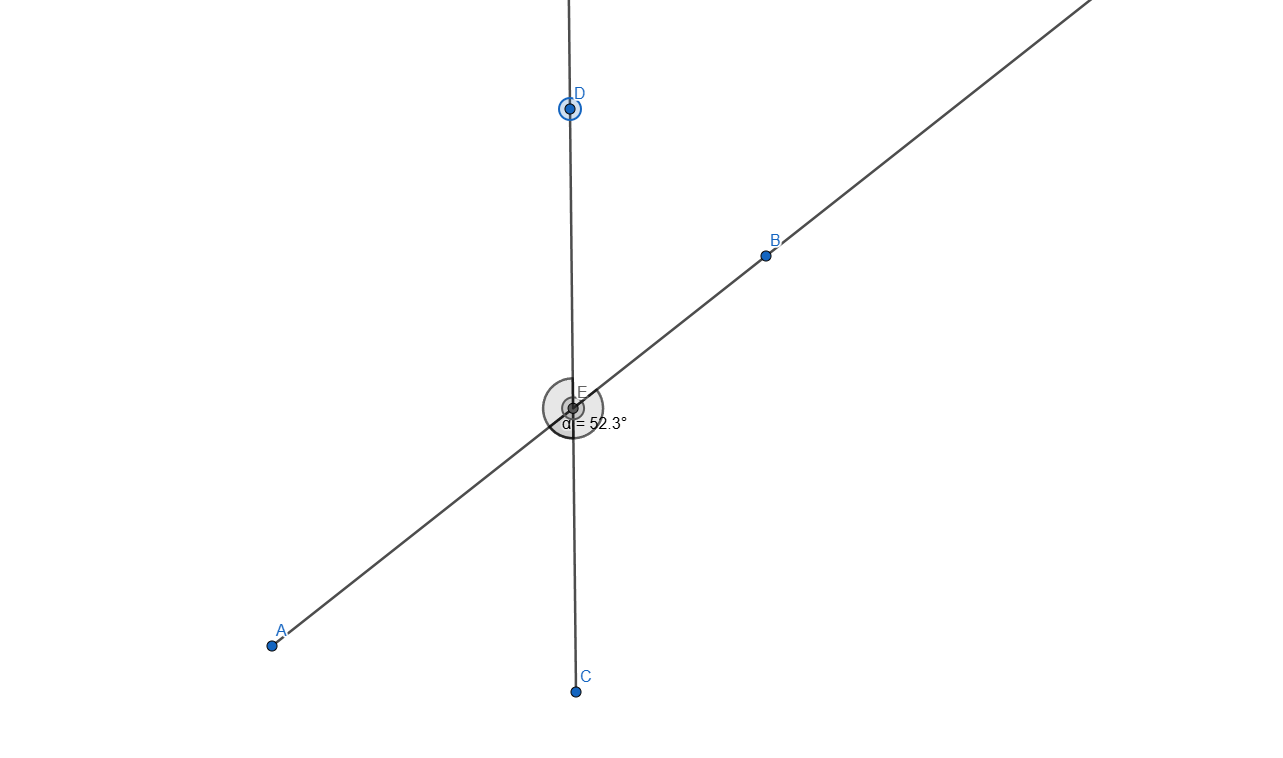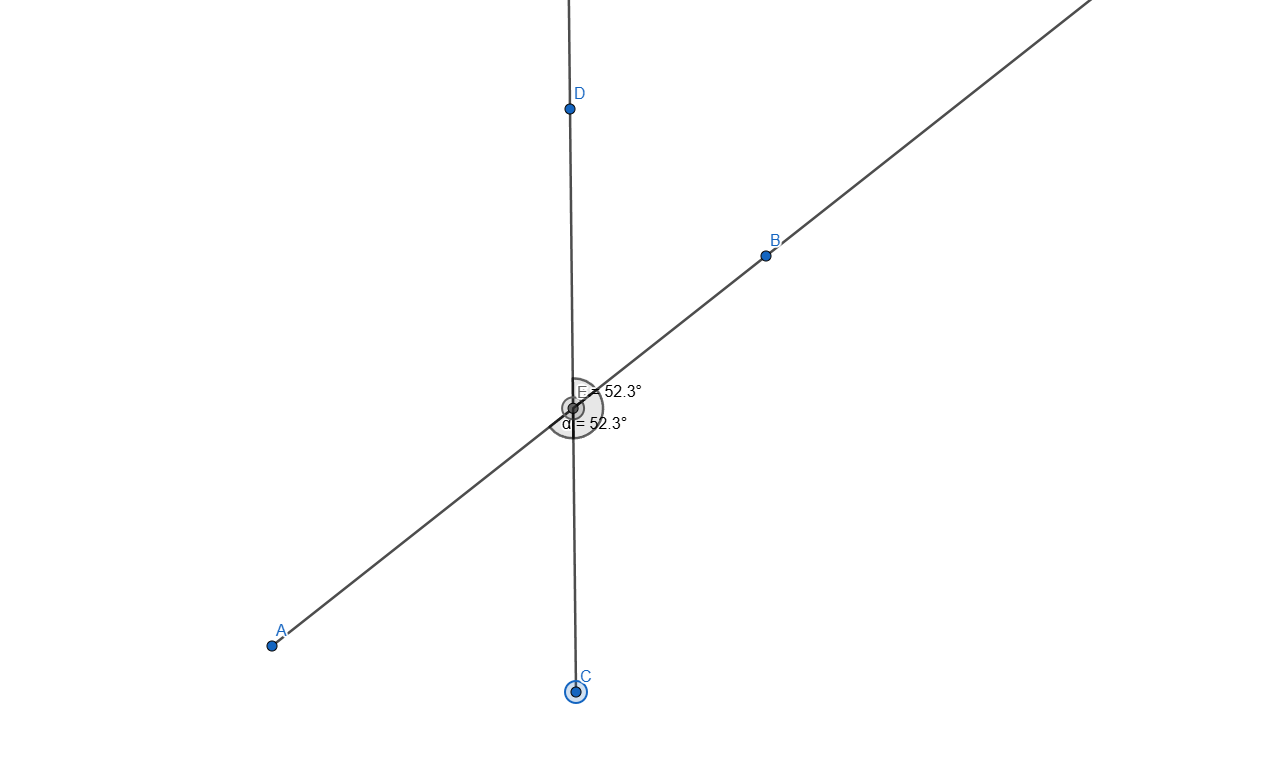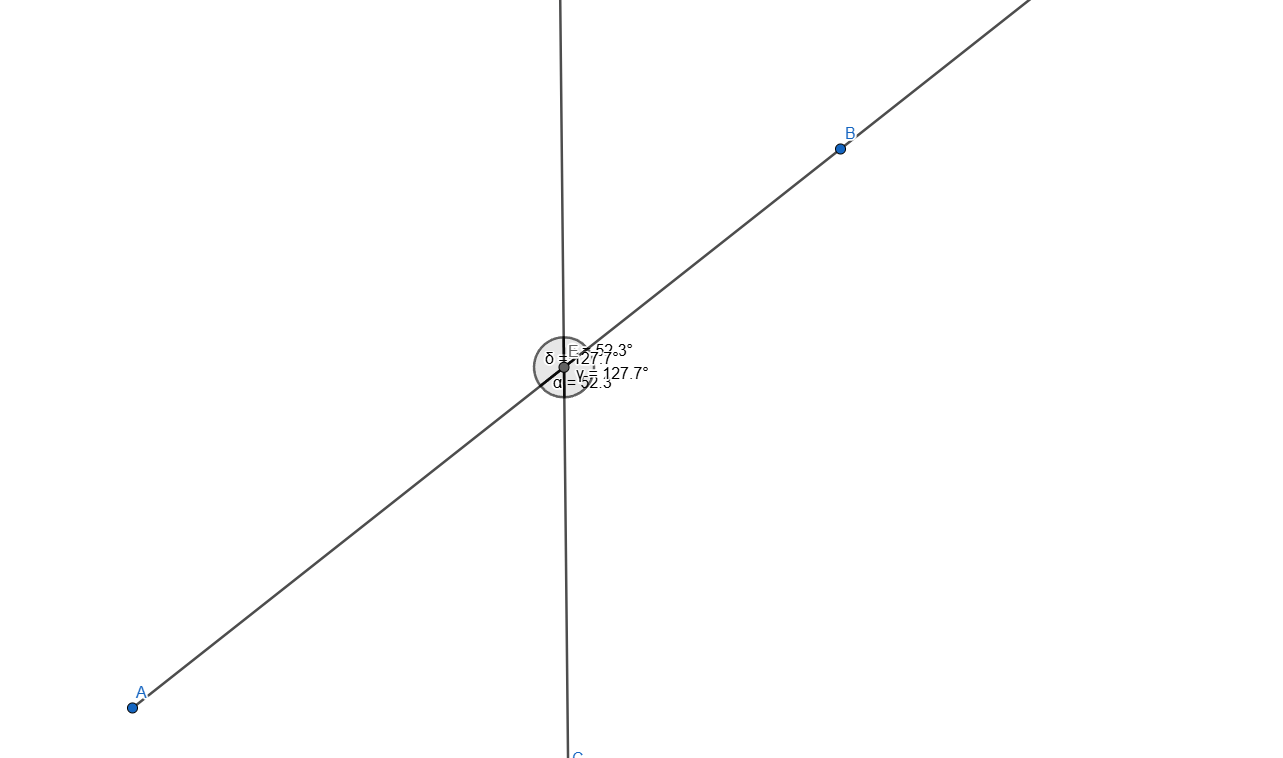
Adding some stylization and we get the following angles:

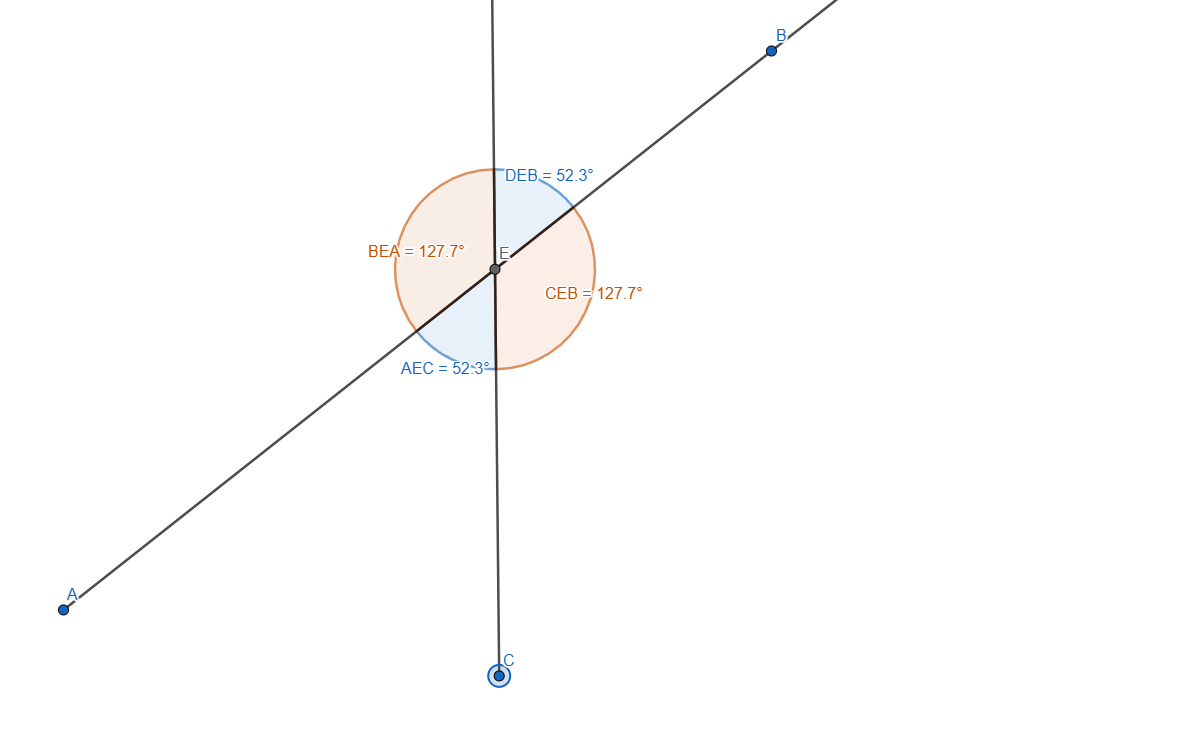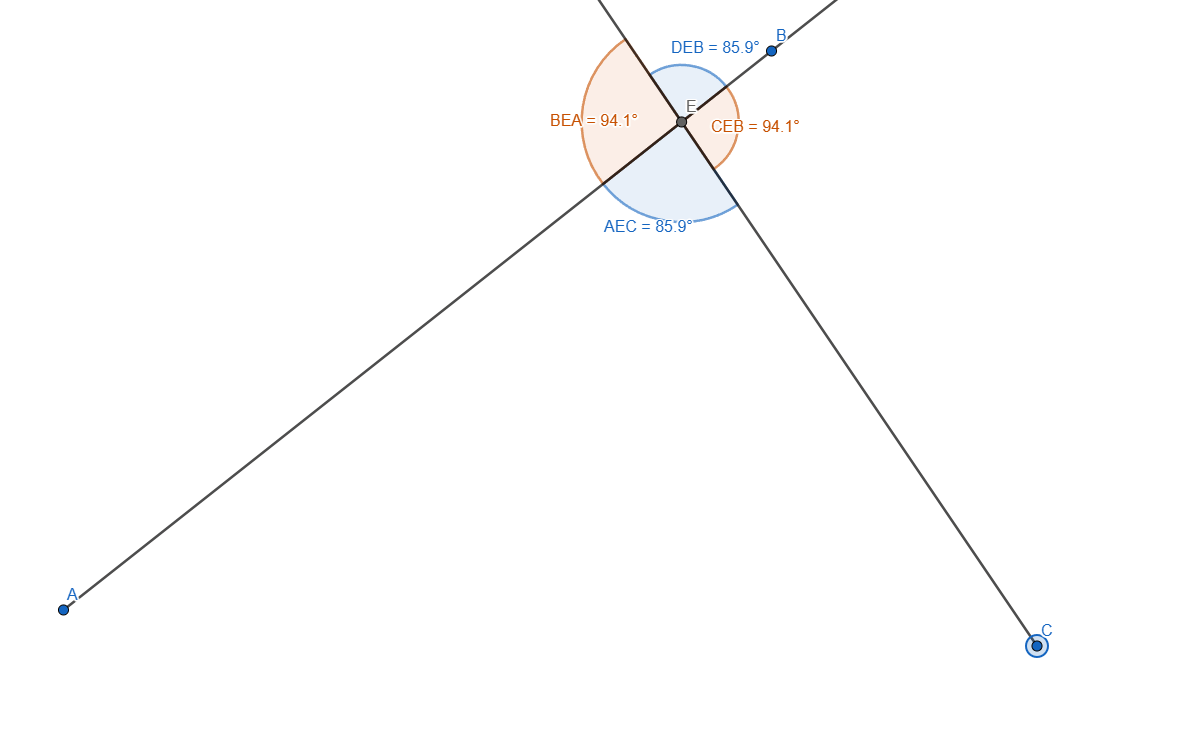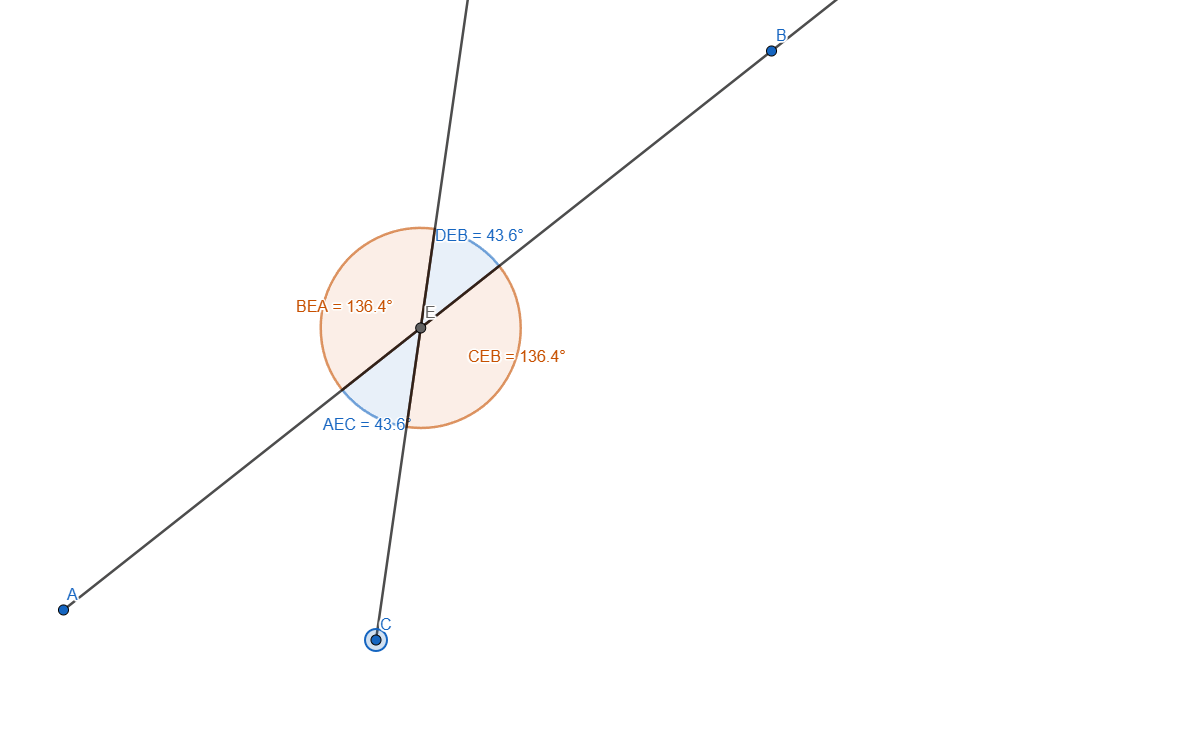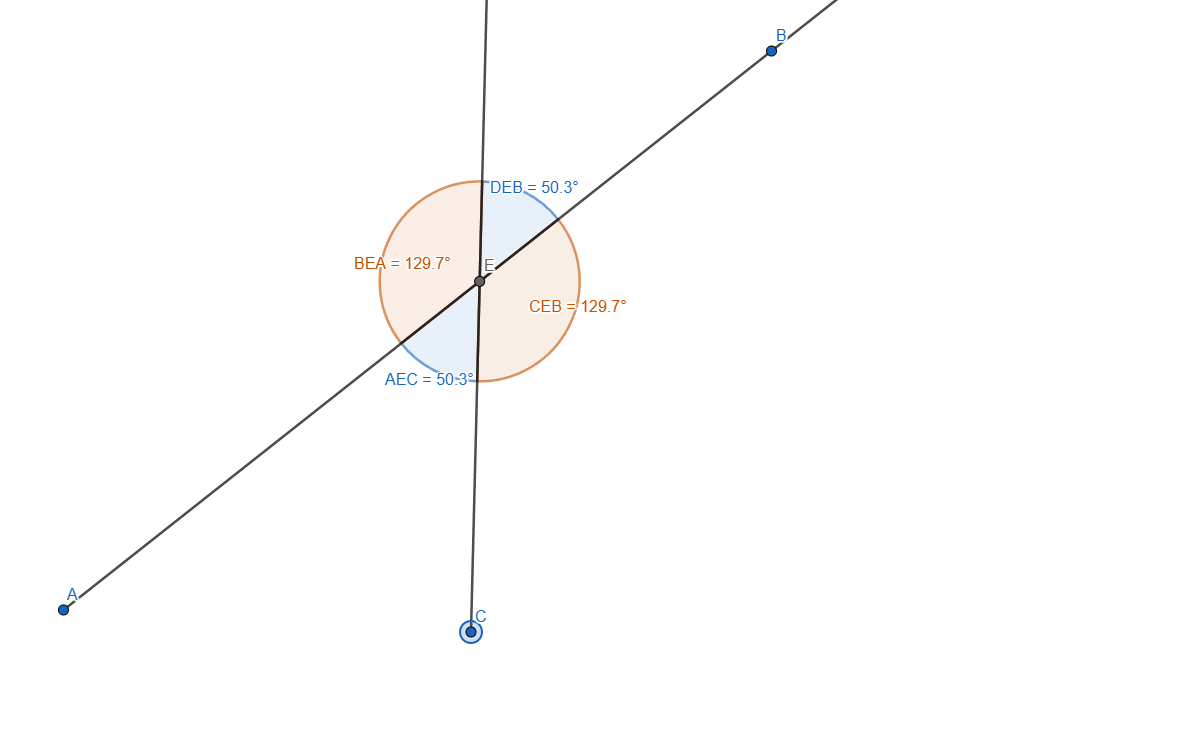
You can see the opposed angles have the same value.

• Construct parallel lines and perpendicular lines.

• Construct two lines intersected by a third line (a transversal). Label the angles on the figure (using letters, numbers, or colors). Name the pairs of angles that have special names.

---

Parallel Lines

Two or more Lines are considered to be parallel if the distance between them is always constant, this means that no matter how far we extend those lines they will never intersect.

To construct parallel lines we need to start with a simple Line, after we draw the Line we need to pick a Point outside the Line we just drew. Now we take the Parallel Line Tool, select the Point we've just added and click our Line, this will draw a new Line through our created Point, Line that is parallel with the Line we created in the first place.

Live example:

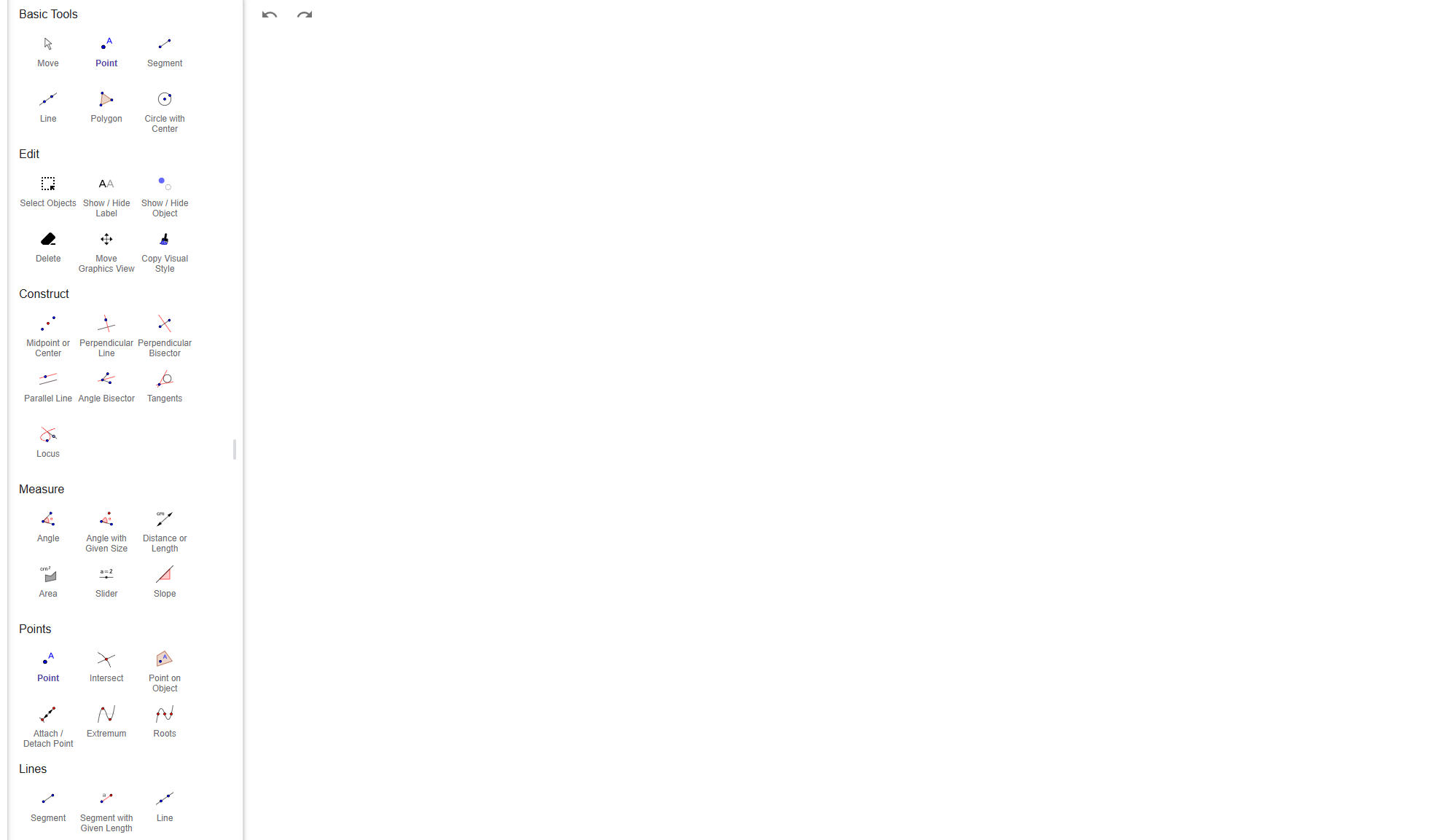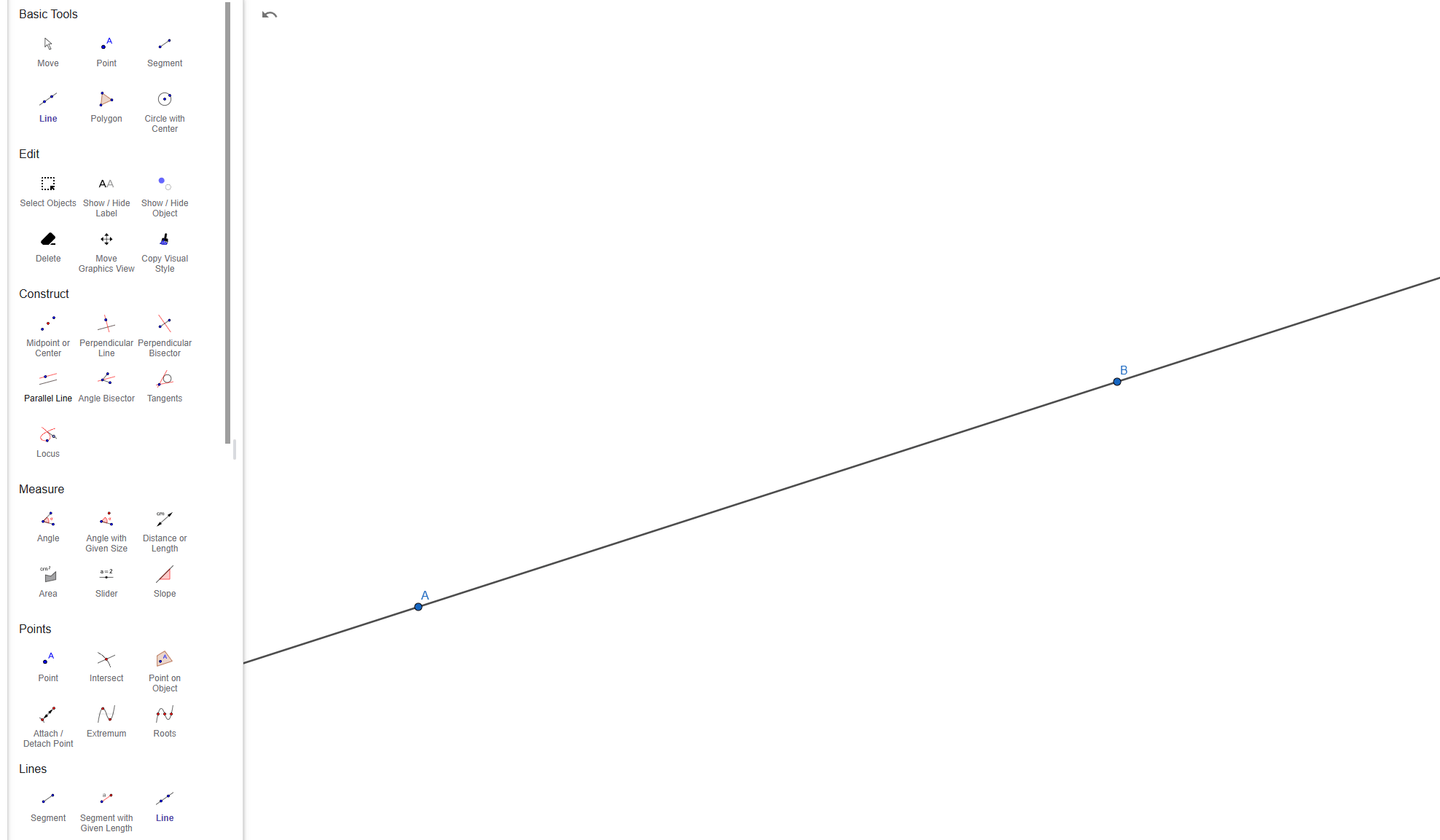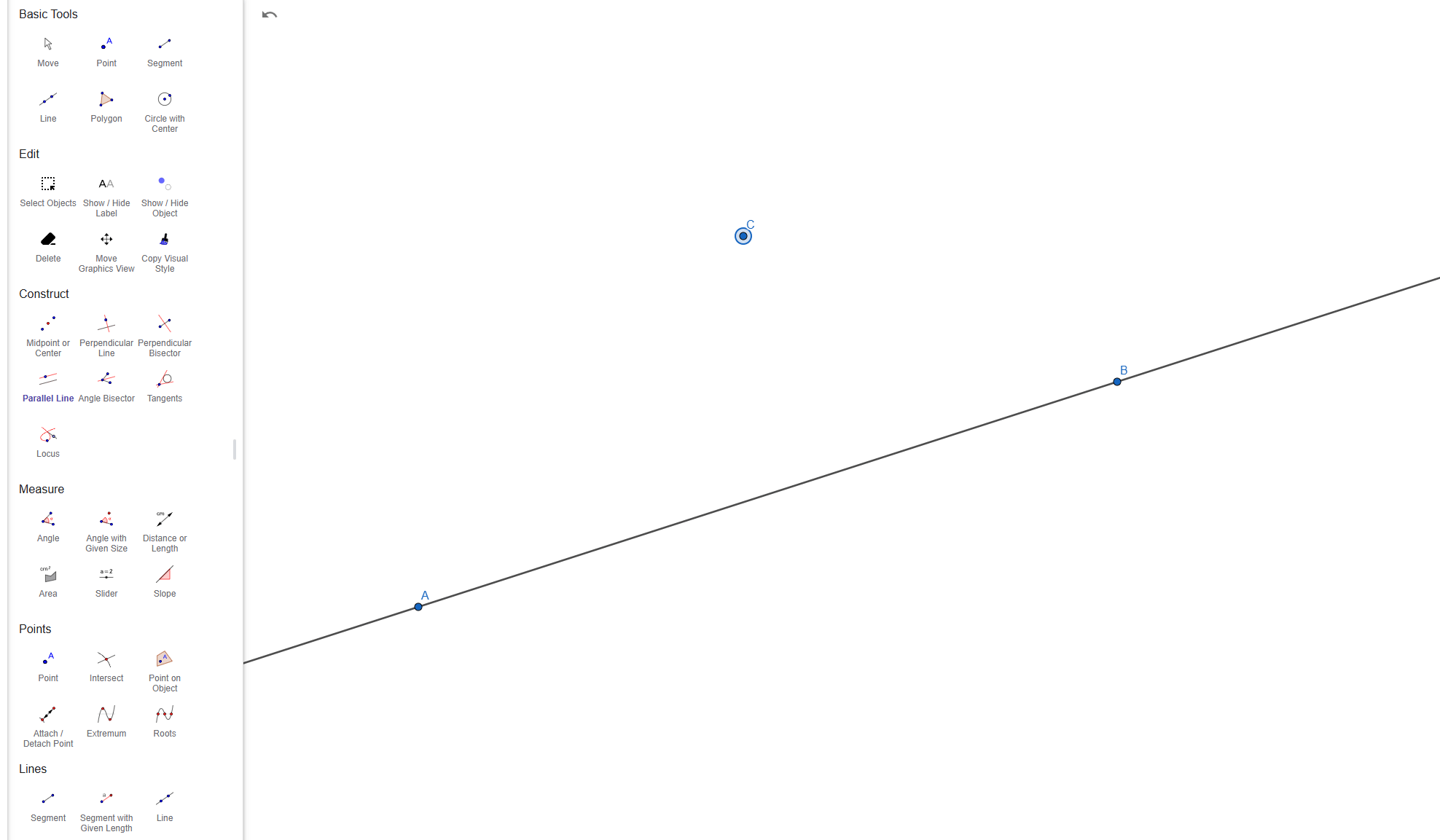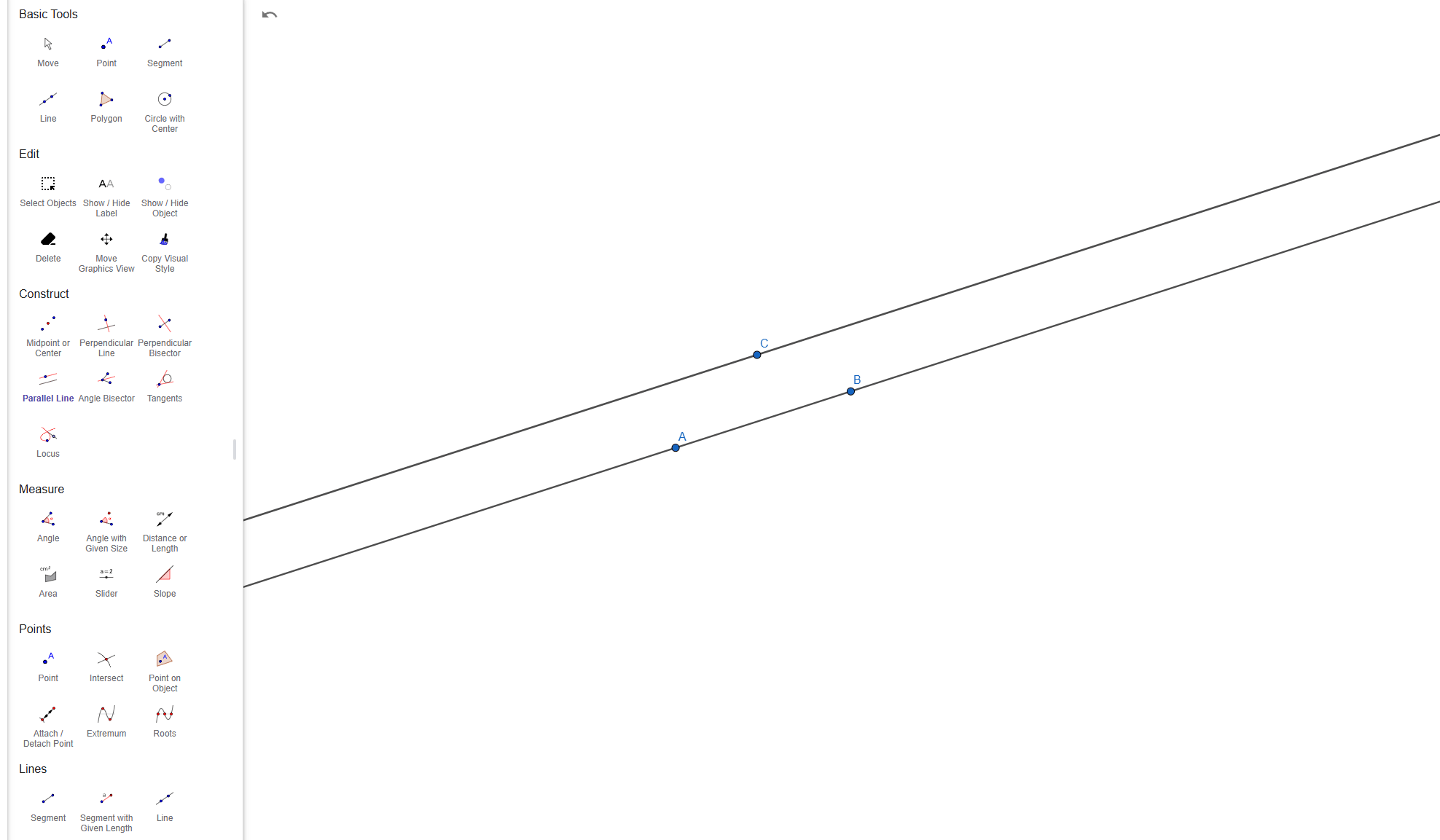
Perpendicular Lines

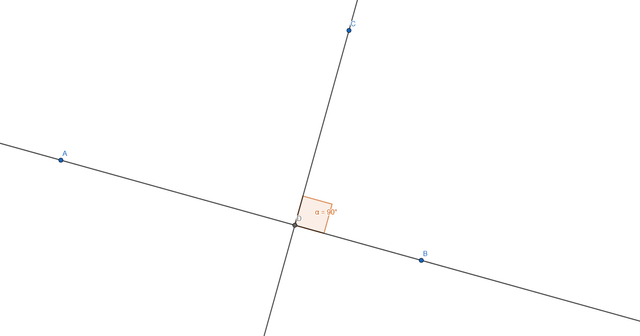
Two Lines are being considered perpendicular when the intersection of those 2 Lines created a 90 Degrees angle.

Ton construct two perpendicular Lines we'll apply the same logic as we did for parallel ones, we start by creating a Line, we pick a Point outside of it and using the Perpendicular Lines Tool we click the point and line and it will generate a new Line that is Perpendicular to the one we created before.

We can also do an Angle check to see the value, in this case you can see it's 90 degrees:

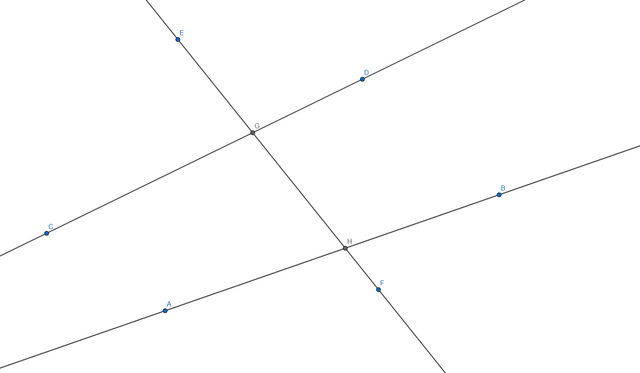
• Construct two lines intersected by a third line (a transversal). Label the angles on the figure (using letters, numbers, or colors). Name the pairs of angles that have special names.

Lets draw the lines first:

Now we will add some points at the intersection of the lines:

Now everything is ready to add the Angles and also add some stylization:

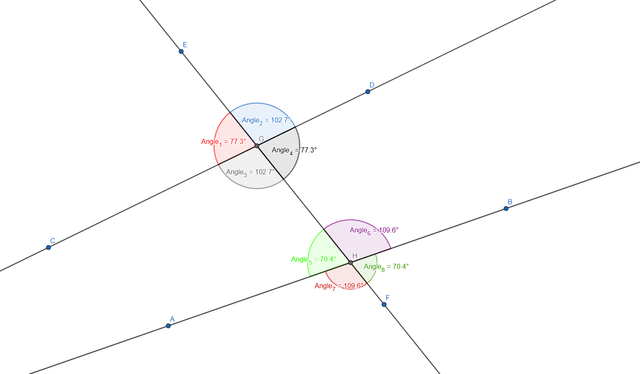
Let's create a table with the special angles:

Type of Angles	Angles
Vertical Angles	(Angle1 - Angle4) (Angle2 - Angle3) (Angle5 - Angle8) (Angle6 - Angle7)
Adjacent Angles	(Angle1 - Angle2) (Angle1 - Angle3) (Angle3 - Angle4) (Angle2 - Angle4) (Angle5 - Angle6) (Angle5 - Angle7) (Angle7 - Angle8) (Angle6 - Angle8)
Interior Same sided Angles	(Angle3 - Angle5) (Angle4 - Angle6)
interior Different sided Angles	(Angle3 - Angle6) (Angle4 - Angle5)
Corresponding Angles	(Angle1 - Angle5) (Angle2 - Angle6) (Angle3 - Angle7) (Angle4 - Angle8)

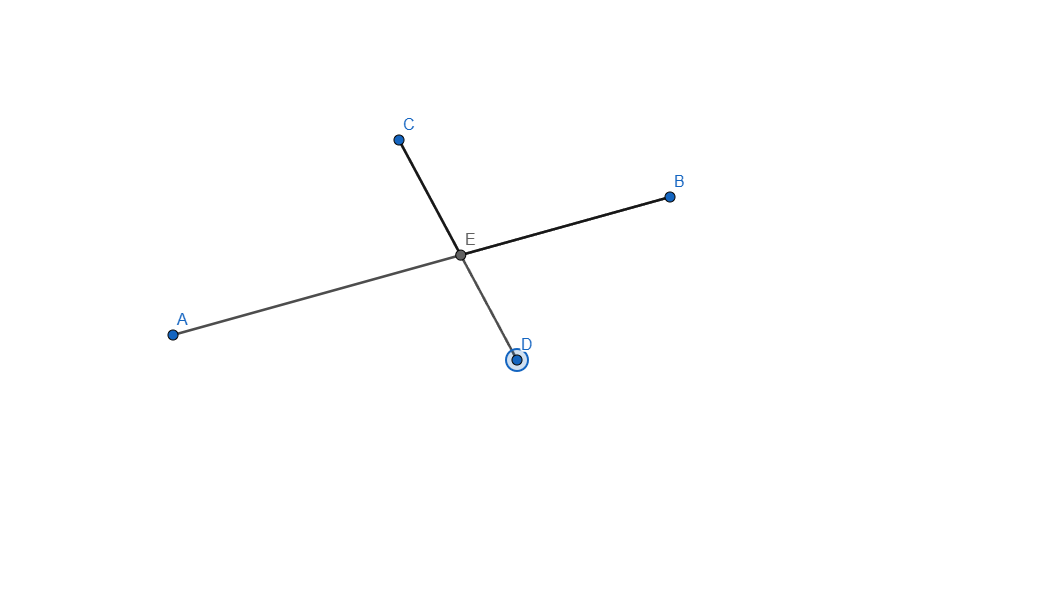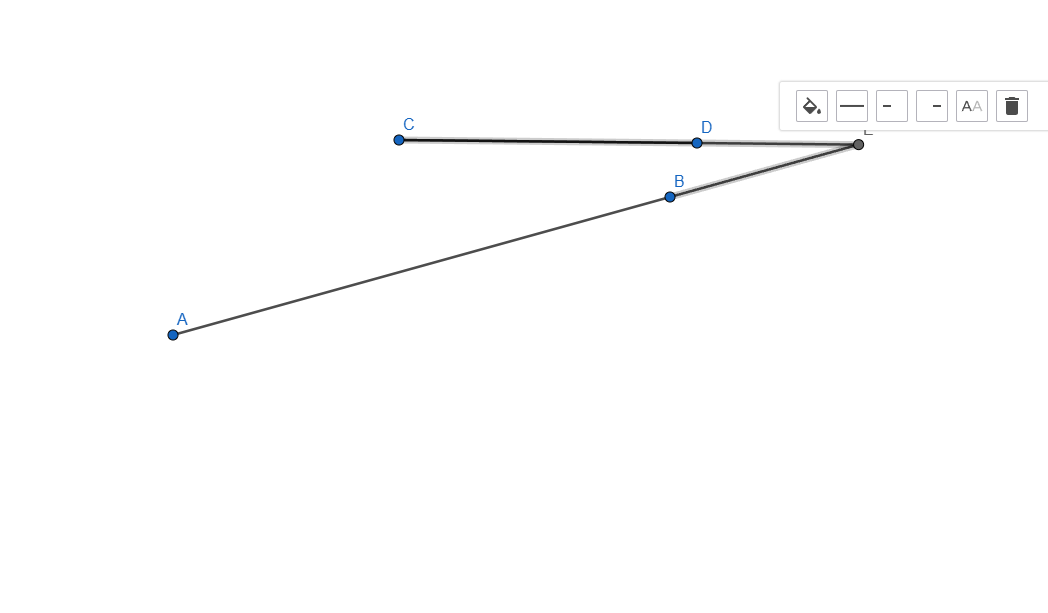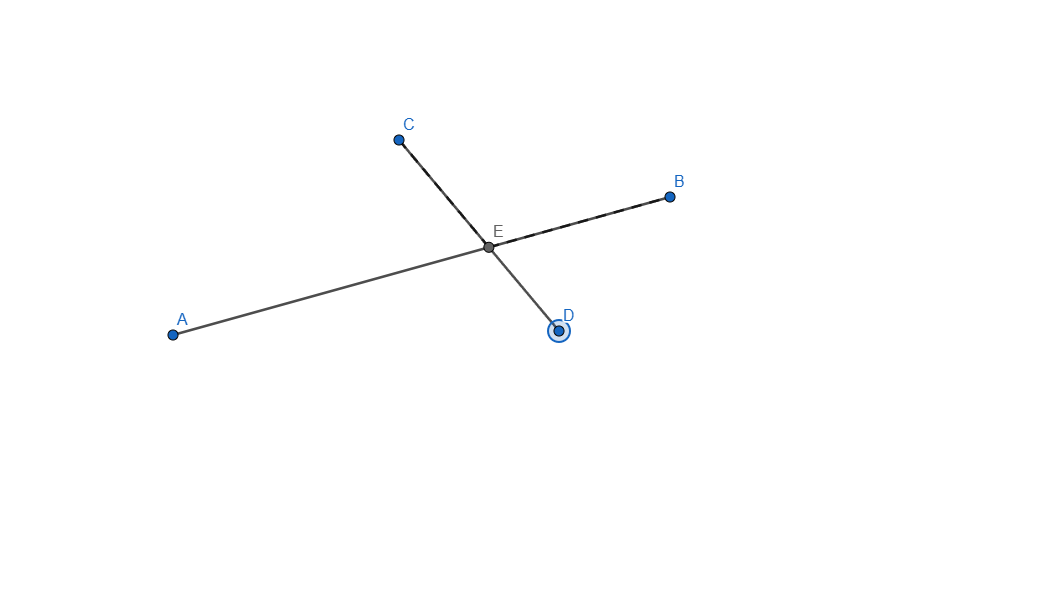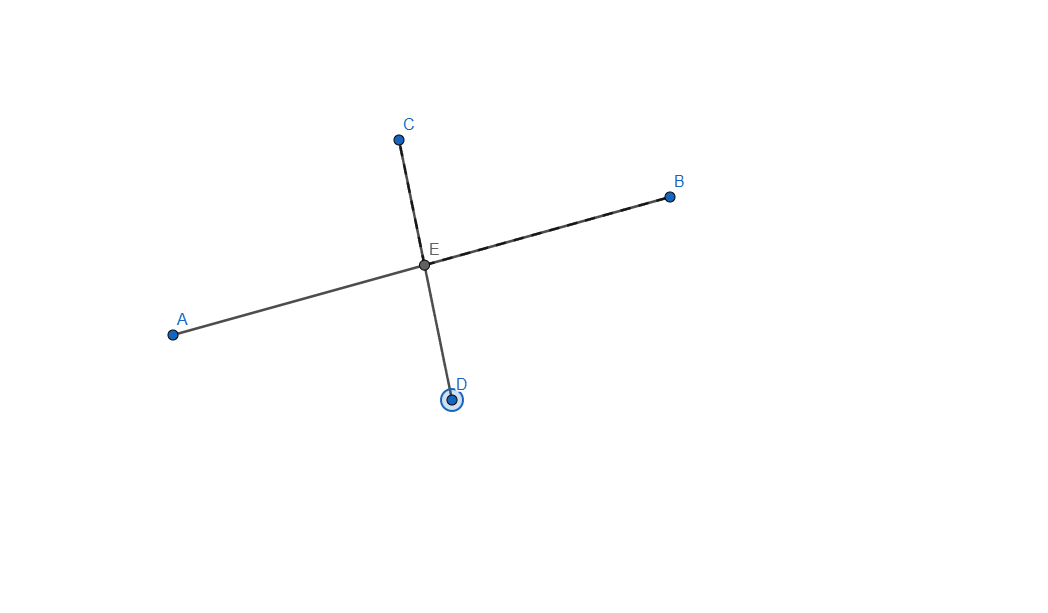
• Construct the intersection of two segments. Ensure that the intersection point is always displayed, even if it does not lie on the segments themselves. If the intersection point lies outside the segments, represent this with dashed lines.

---

This was one of the hard tasks, I think I looked through all the settings trying to find some sort of Project option but couldn't find anything, after a couple of hours I think I did it:

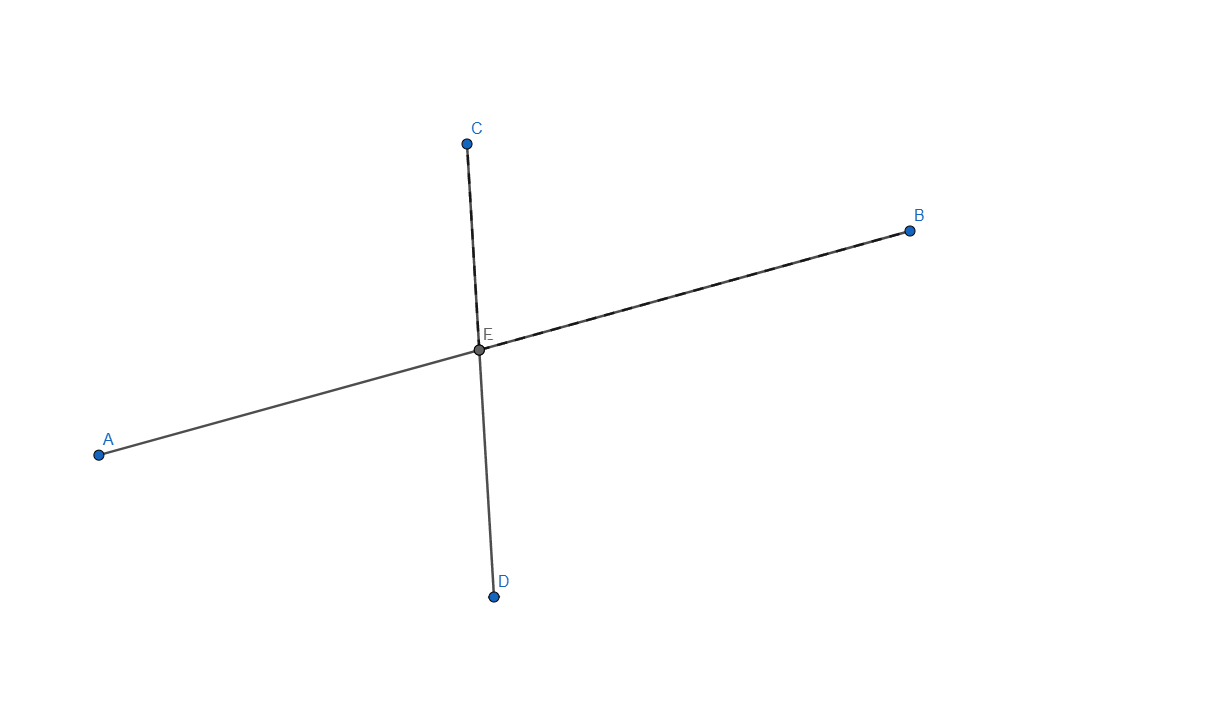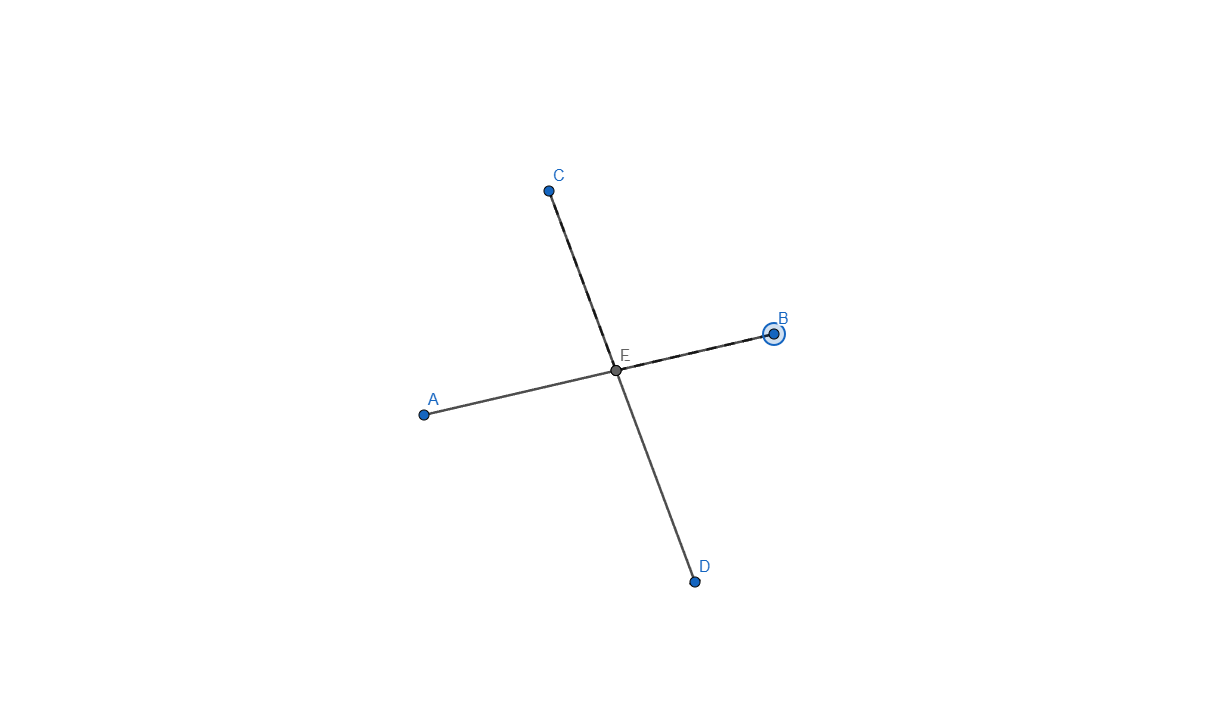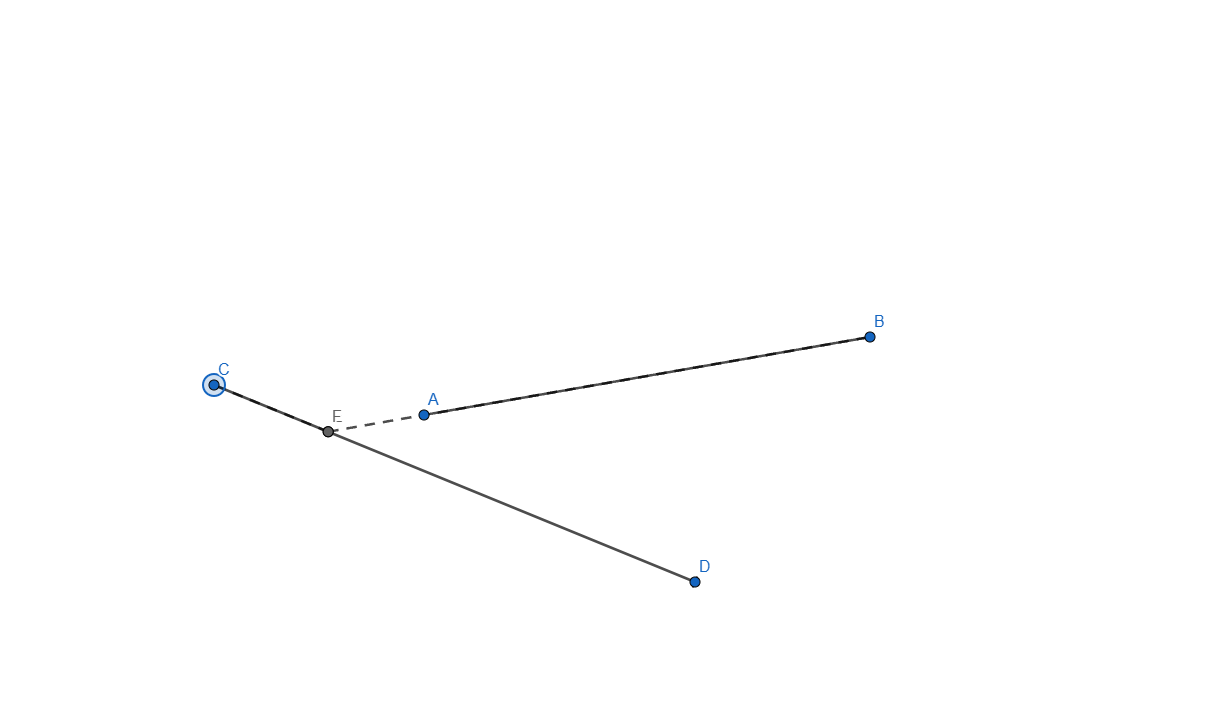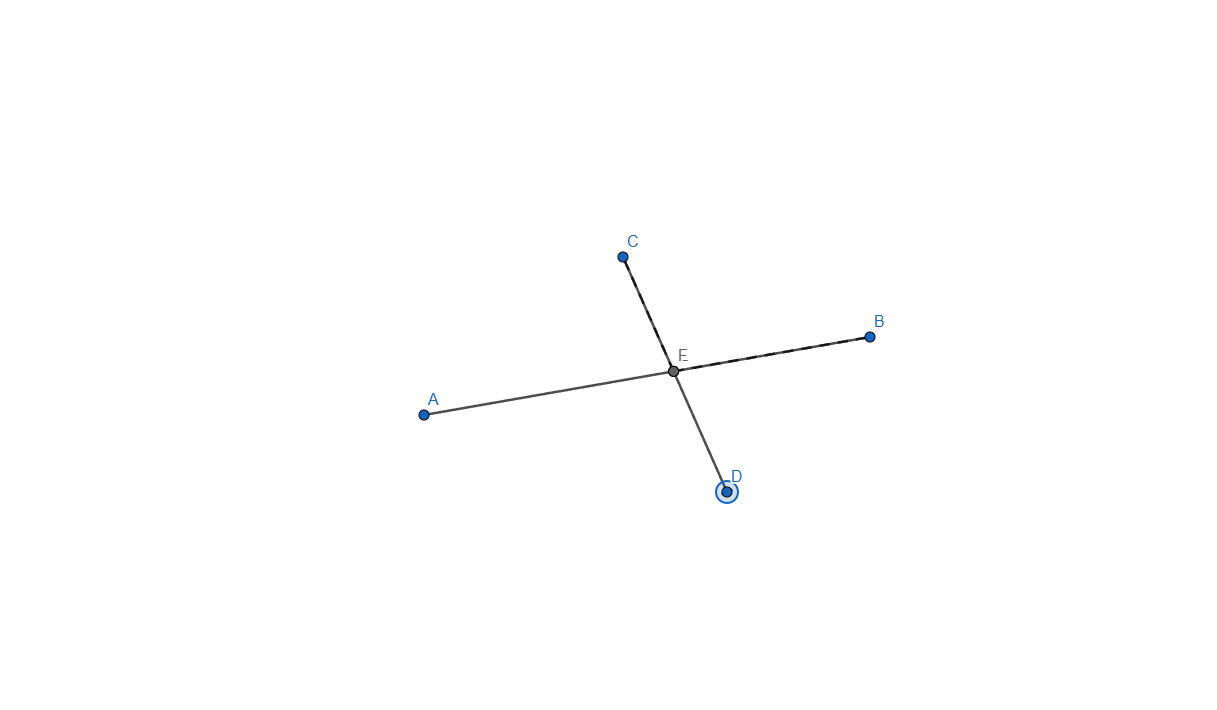
Now let me explain how I did it, started by creating the two segments needed for this task and applied an intersection point between them. I selected each line and in the Basic tab of Settings I checked the box that says "Allow Outlying Intersections". In this point when we are moving any of the segment end the intersection point will move, even outside the lines but it won't show the dashed line.

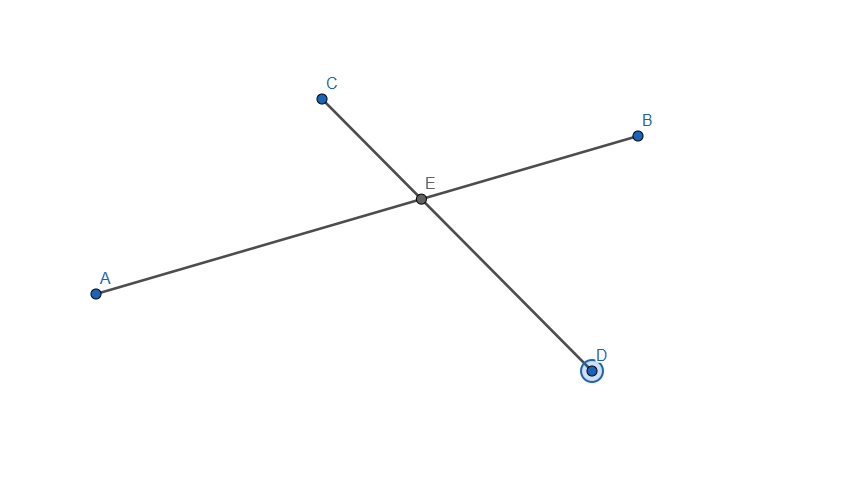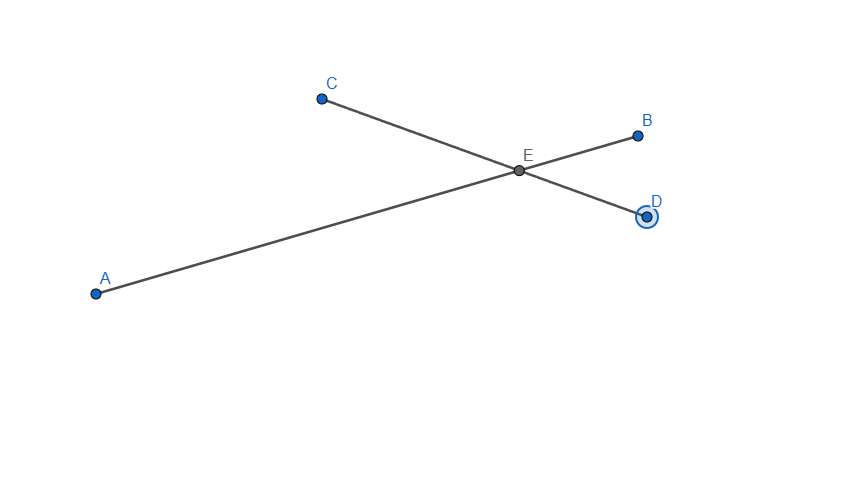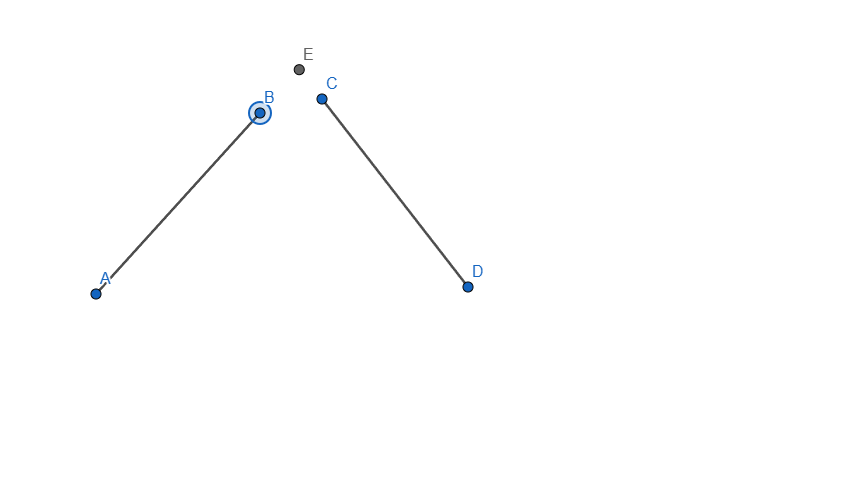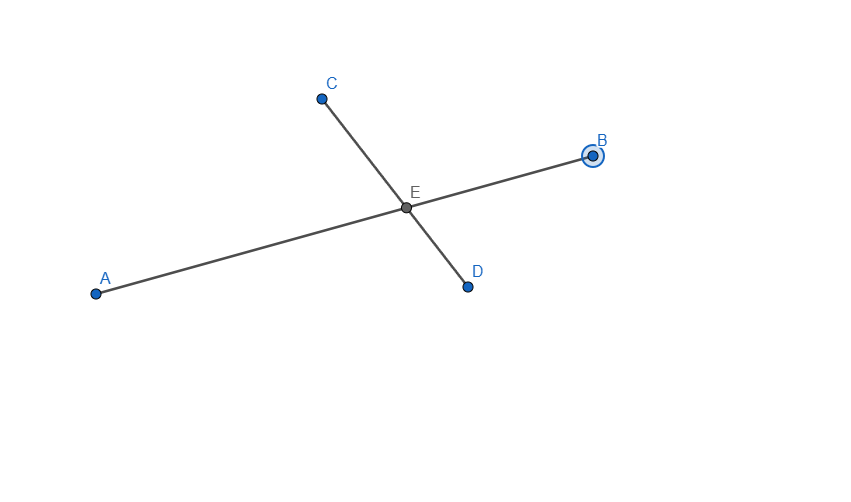
From this point all that was left to do what to add the dashed line, for this one I added another segment from E to B and from E to C and set it to be dashed line, now because the dashed line overlaps the normal one it is not visible unless you move it outside, once moved outside the dashed line shows as a projected path to the intersection of our two segments.

---

That was it for this week's geometry, in the end I'd like to invite @titans and @mojociocio to participate, I remember @mojociocio also took part in last season math challenges, so here's a new one for ya!

Thank you, I am wishing you a great day!