25-11-2024 - Education - Linear Algebra - Projective Transformations [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
25-11-2024 - Education - Linear Algebra - Projective Transformations [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytic geometry or linear algebra
(code notes: MOD-60)
Projective transformations
Technical definition
Consider the n-dimensional projective space
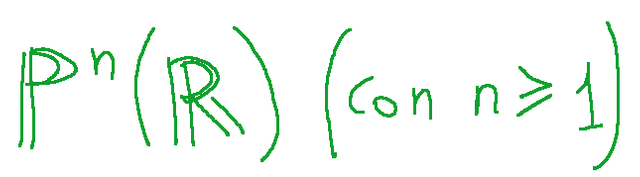
Let
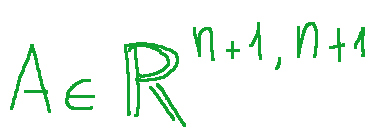
be an invertible matrix.
The application shown below
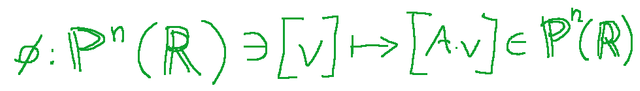
is called a projective transformation. The matrix A is denoted by
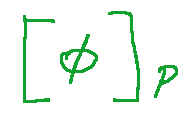
Other definition
Projective transformations in analytic geometry are transformations that preserve the projective properties of geometric figures, such as the alignment of points. These transformations are the heart of projective geometry, an extension of Euclidean geometry that deals with invariant properties under projections.
We can say that a projective transformation is a one-to-one correspondence between points in a projective space that can be expressed by a linear transformation between homogeneous coordinates.
Properties of projective transformations
-Invariance of alignment
-Invariance of the harmonic ratio
-Non-conservation of distances and angles
-Inclusiveness
Example exercise
We can find a matrix that represents the projective transformation that extends the affinity
Projective transformation that extends affinity
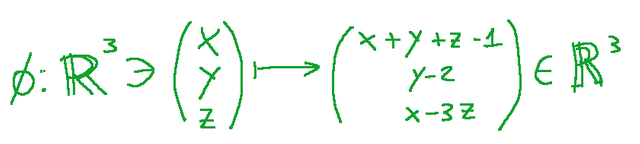
Matrix
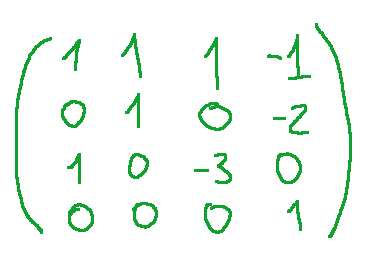
Conclusions
A simple projective transformation is the central projection of points from one plane onto another plane along lines passing through a fixed point (the center of the projection). This can be described mathematically by a matrix.
Question
I think that analytical geometry can be a good exercise for our brain, but at a certain point it becomes too complicated, what do you think?

[ITALIAN]
25-11-2024 - Education - Algebra lineare - Trasformazioni proiettive [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-60)
Trasformazioni proiettive
Definizione tecnica
Si consideri lo spazio proiettivo n-dimensionale
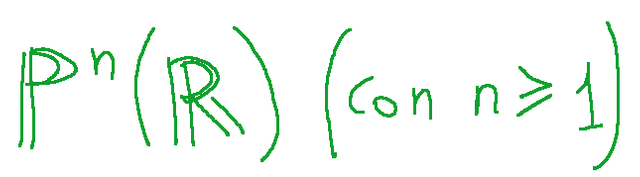
Sia
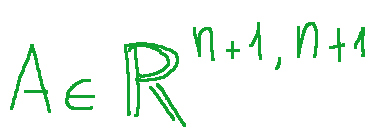
una matrice invertibile.
L’applicazione mostrata qui di seguito
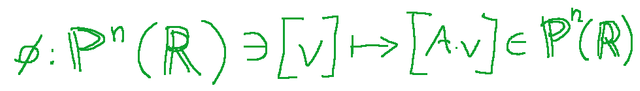
è detta trasformazione proiettiva. La matrice A è indicata con
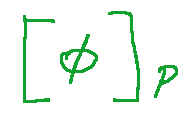
Altra definizione
Le trasformazioni proiettive in geometria analitica sono trasformazioni che conservano le proprietà proiettive delle figure geometriche, come l'allineamento dei punti. Queste trasformazioni costituiscono il cuore della geometria proiettiva, un'estensione della geometria euclidea che si occupa di proprietà invarianti sotto proiezioni.
Possiamo dire che una trasformazione proiettiva è una corrispondenza biunivoca tra punti in uno spazio proiettivo che può essere espressa mediante una trasformazione lineare tra coordinate omogenee.
Proprietà delle trasformazioni proiettive
-Invarianza dell'allineamento
-Invarianza del rapporto armonico
-Non conservazione delle distanze e degli angoli
-Inclusività
Esempio di esercizio
Possiamo trovare una matrice che rappresenta la trasformazione proiettiva che estende l’affinità
Trasformazione proiettiva che estende l’affinità
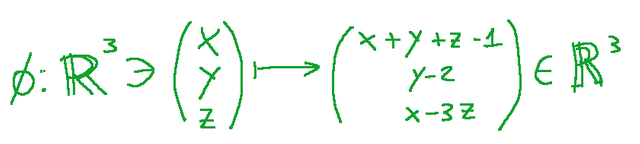
Matrice
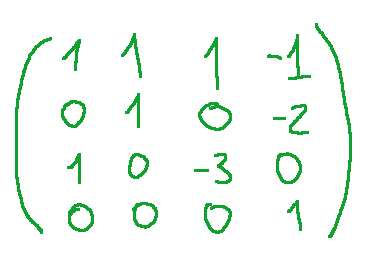
Conclusioni
Una trasformazione proiettiva semplice è la proiezione centrale di punti da un piano su un altro piano lungo linee che passano attraverso un punto fisso (il centro della proiezione). Questa può essere descritta matematicamente da una matrice.
Domanda
Io credo che la geometria analitica possa essere un buon esercizio per il nostro cervello, ma ad un certo punto diventa troppo complicata, voi che ne pensate?
THE END
Algebra is a bit difficult for me, I don't understand Algebra very well, you have explained Algebra party very well, anyone reading your post can understand it very well, thanks a lot for sharing this beautiful post with us.
Thank you for your kind words. Sometimes I realize that I could describe what I explain even better.
Quando saturiamo il nostro cervello reagisce in modo diverso. Ho notato che non riposando abbastanza a volte dimentico qualcosa che ho fatto molte volte. Il nostro cervello potrebbe richiedere più riposo di quello che gli forniamo.
Io noto che per il nostro cervello più passano gli anni e più c’è bisogno di riposo
@tipu curate 2
Upvoted 👌 (Mana: 2/7) Get profit votes with @tipU :)
Thanks for stopping by, your support is much appreciated.