Why do you need Portfolio Optimization?
During the immediate past bull trend for technology stocks, a friend of mine told me he bought Tesla (TSLA), Facebook (FB) and Apple (AAPL) to take advantage of the trend as he couldn't decide which one of the tech stocks to buy. For those knowledgeable in Finance, you will understand why I nearly fell off my chair on hearing this. After questioning him for almost an hour on his rationale for committing this cardinal sin in finance and whether he has never heard of portfolio theory, I came to finally realize why common sense is not always common - people assume they know what they don't really understand. Hence, for today, and after a very long while, I decided to do a post on portfolio optimization and why you always need to consider it in all your investing. Like all my posts, I'll try to minimize all the technical jargon and make it so much easier for anyone to understand. So let's get started - why do you need portfolio optimization?
There are two competing sides to the market - Return vs. Risk
When my friend was thinking about investing in the tech uptrend, he was actually only thinking about one side of the market - the return side - but was unfortunately blind to the other side of the market - risk side. This is actually a common mistake made by novice investors. But the market is like a 2 sided-coin. Just as it can deliver remarkable returns, it can also carry significant risks. All investors should be thinking of both return and risks when thinking of investing. Now, whenever there are two opposing sides to any problem, there is always a middle ground to be sought. Finding that middle ground is the central thesis of modern portfolio theory (MPT) as proposed by Markowitz and his collaborators. While the mathematics behind MPT can be daunting, the fundamental principle behind MPT is that one should always maximize returns for every unit of risk undertaken in the market or one should minimize risk for every unit amount of return being sought. The ratio of returns to risk is the most popular objective function for portfolio optimization. Infact, it is so popular that it has a name - Sharpe Ratio - named after its inventor, Williams Sharpe.
Returns are averaged, risk is not
Having established the objective function for portfolio optimization as the ratio of return to risk, this next part lays out why selecting just any stocks based solely on to create your portfolio is a very bad idea. Imagine you have a portfolio of just two securities - AAPL and FB that have gone up in recent times. Also imagine that because you are a naive investor, you decide to not listen to me and go ahead to split your available funds such that you bought 50% APPL and 50% FB in dollar terms. Also, (just for the sake of this analysis) that APPL and FB have the same expected returns. Now, your portfolio expected return is simply the weighted average returns of both AAPL and FB which will be exactly the expected return of either AAPL or FB because of our initial assumption of both stocks having the same return.
At this point, there is really no harm done. If you only consider returns, there is really no reason to have a preference for two stocks that have the same expected return. You either pick one or split your funds 50-50. Everything changes however, when you consider the risk side of the equation. This is because in addition to just averaging out the risk (more complicated because the terms are squared but that is a technicality that is not necessary for our purposes) of both portfolios, you also need to add a term that accounts for the return correlation of both securities.
This is the key! So for our example where we've assumed both APPL and FB having the same return, you need to add to the risk average in the denominator a term that accounts for perfect correlation of the two stocks! Now I promised there will be no maths, but for those who are mathematically inclined, you realize that if you add a term to the denominator of any fraction, it gets bigger, making the entire fraction smaller! So by buying two stocks that are positively correlated with similar returns, you are invariably disobeying the tenets of MPT and not maximizing your returns per unit risk taken. Or, you are taking on more risk than necessary for the same return.
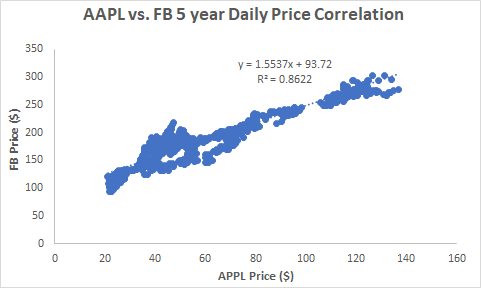
One might be wondering how correlated can AAPL and FB stocks really be? I've plotted the last 5 years of APPL vs. FB returns in the figure below and you can see that both stocks are significantly correlated with an R2 value of 0.86. Generally, stocks in the same industry or sectors are expected to be positively correlated. Since AAPL and FB are in the technology sectors, it is no surprising that their returns are this correlated.
So is this all doom and gloom? How can one utilize this knowledge to assemble a portfolio that maximizes returns while minimizing risk? The answer to this question is what MPT is all about but to give you a hint, since the correlation term is additive, is there a way to negate it? You guessed it! All we need to do is instead of selecting selecting stocks that have returns that are positively correlated, we can select stocks that have similar returns but are negatively correlated or less positively correlated. Can you find 2 stocks that are negatively correlated but with similar returns? Give it a try. Hint: Think cross industries or across sectors. I will love to hear what you came up with.

I think is important not to complicate too much on the analysis. You can simply invest in an ETF and forget about it.
Good point @chesatochi, however ETFs are specific investment vehicles and may not be as diversified as an investor may want. In such a case, the investor may apply the same technique with multiple ETFs. Thanks for the comment!
My pleasure. :)