Integrales indefinidas directas con ejercicio
La integral se utiliza para conocer el área bajo la curva de una función. Es la antiderivada es decir la operación inversa de una derivada. Y su simbología es:

Existen dos tipos de integrales: Las definidas y las indefinidas. Su diferencia más significativa es que la integral definida presenta un intervalo de integración cerrado y finito, es decir un área limitada de la gráfica de una función, mientras que las indefinidas no presentan ningún tipo de intervalo.
Para resolver una integral indefinida se utilizan uno de los siguientes 5 métodos:
• Integración directa.
• Cambio de variable.
• Integración por partes.
• Sustitución trigonometríca.
• Fracciones parciales.
La integración directa, es un método para integrales que podrían catalogarse como "simples" estas pueden resolverse con la tabla de integrales básicas o con la utilización de recursos algebraicos como: división de polinomio, descomposición en suma de fracciones o con reglas de potenciación para posteriormente usar la tabla.
Esta es la tabla de integrales básicas:
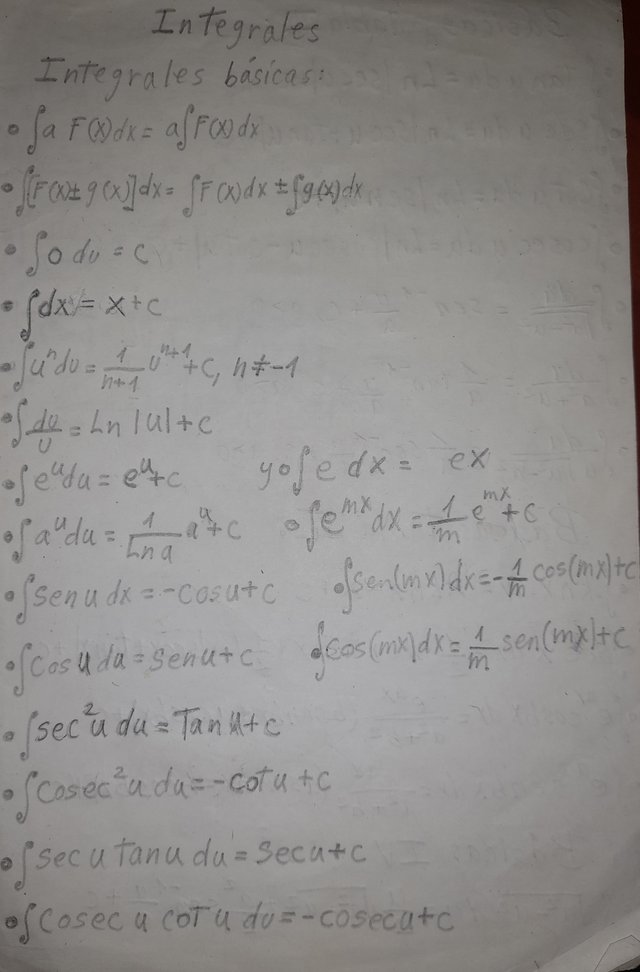
Ahora, les explicaré como resolver un ejercicio de integral directa con logaritmos y exponenciales:
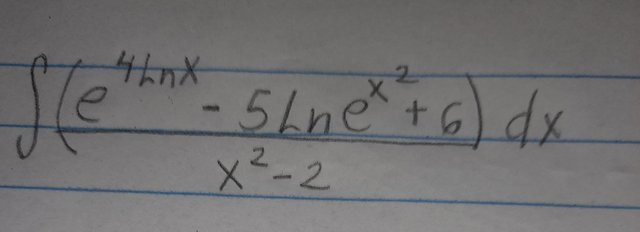
Primero, vamos a reescribir el "4lnx" como "lnx^4" y tendremos por propiedad de logaritmos y exponenciales que "ln(e^(x^2))" va a ser "x^2".
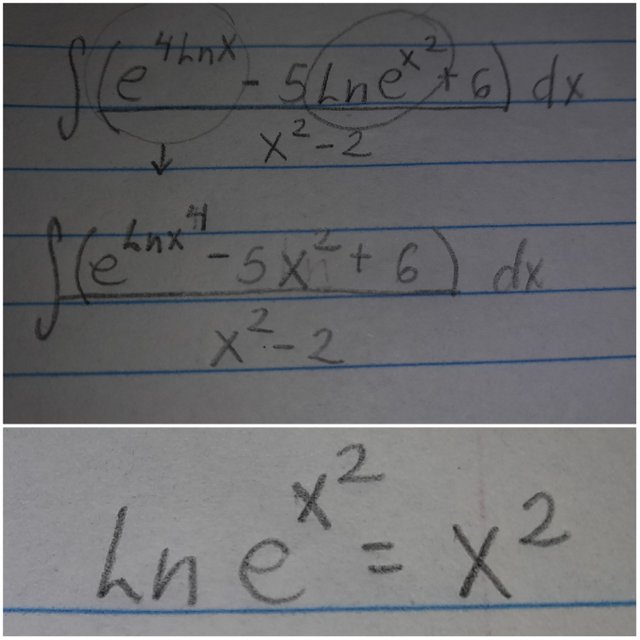
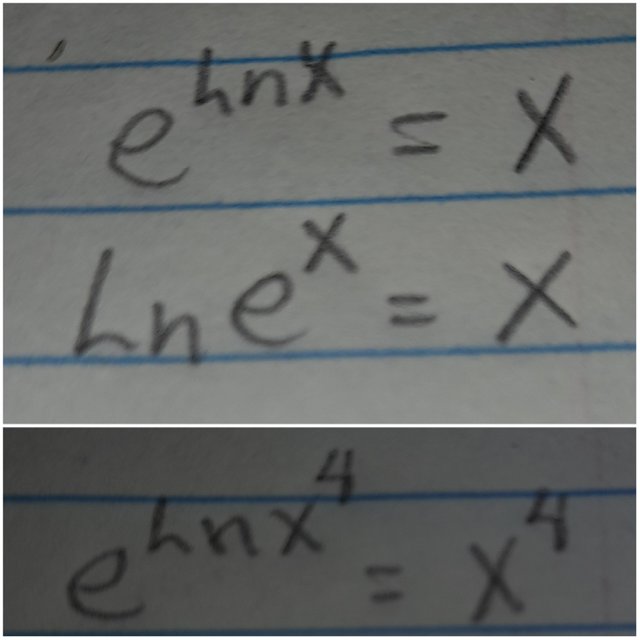
Luego por las propiedades que explique antes tendremos que "e^(lnx^4)" va a ser igual a "X^4". Luego nos queda:
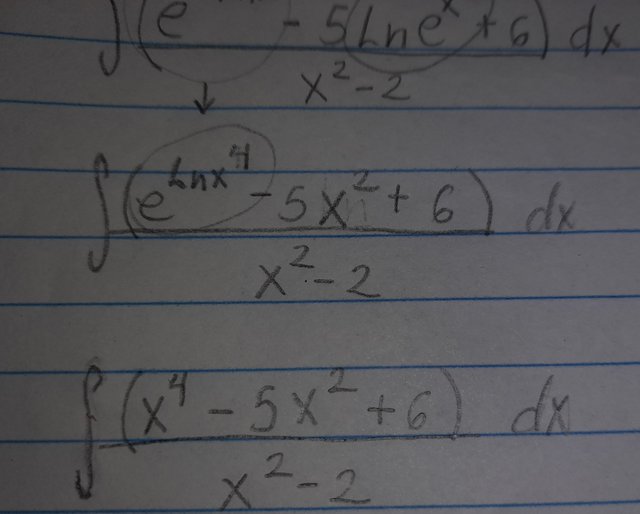
Ahora reescribiendo "x^4" por "(x^2)^2" podemos aplicar una forma de factorización por tanteo:
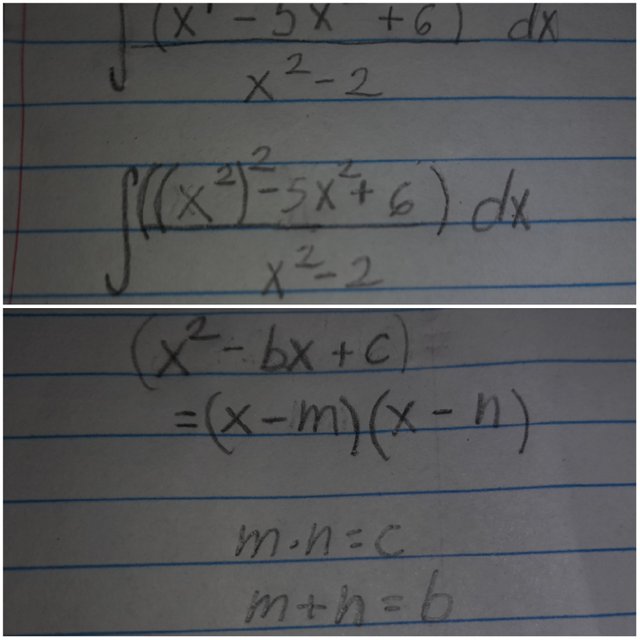
Luego tenemos que para que se cumpla, debera ser m=2 y n=3. Nos queda entonces:
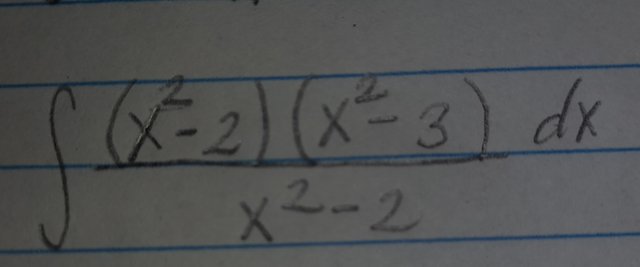
Después eliminamos o dividimos los términos iguales:
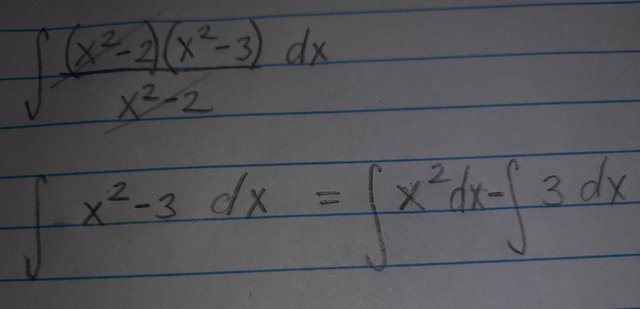
Como ya la hemos simplificado, podemos distribuir la integral y resolver cada uno por separado, para integrar "x^2" y "3" aplicamos las fórmulas de la tabla.
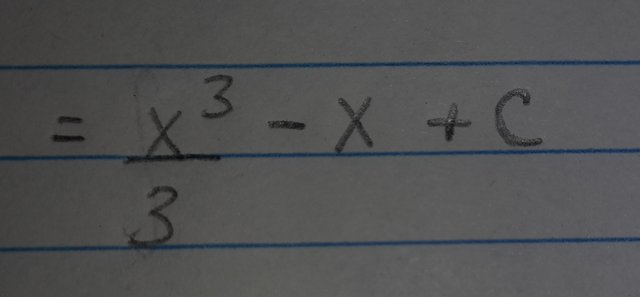
Al final colocamos el sumando "C" necesario en la realización de los ejercicios de integrales, que representa a la suma total de todas las constantes.
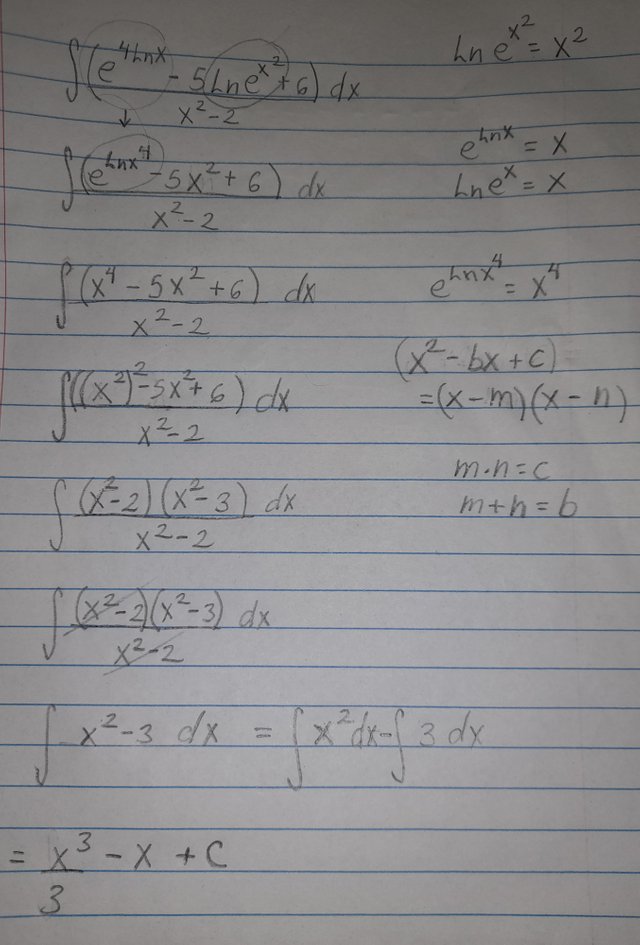
Felicidades amiga tremendo ejercicio 👏que bueno y los términos que usas al señalar cada uno de los 5 pasos
Gracias por compartir.
#onepercent
#venezuela
#affable
Muchas gracias 💖 me alegra que te haya gustado
Gracias a ti, feliz dia.
Aunque no entendí de a mucho te quedo muy bonita toda la publicación.
Feliz dia, muchas gracias primo 💖💫
Excelente! una clase magistral y muy precisa que beneficia a la comunidad. Que bueno que nos demostraras con la practica de este ejercicio tu conocimiento.
Saludos!
Muchas gracias ☺ saludos.