“SLC-S22W5//Polynomial and rational expressions”

deetalka6 (64)Member/verifiedin Steem4Nigeria • 3 days ago

The last time I applied for this, I could remember I didn't do well. So, I decided to apply again. I love mathematics very much and no matter how difficult the problem be, I would try all my possible best to get it right. Even if this won't favour me, I would keep on trying.

Greetings to @khursheedanwar. I've always enjoy your kind of work, even though some questions here seems critical.

That's Mathematics for me

Task 1

Explain difference between Polynomial and rational expressions. Provide examples of each type of system of equation and describe their general forms

S/N	Polynomial Expressions	Rational expressions
1	From your teachings Sir, Polynomial expressions is an algebraic expression that contains variables, coefficients as well as mathematical terms.	Rational expressions is an algebraic expression comprising of two polynomial expression.
2	Polynomial expressions term may be added, subtracted and multiplied but they can't be divided	Rational expression can be added, subtracted, multiplied and also divided

Example of Polynomial expressions: 2x²+3x–4
Examples of Rational expression: (2x²+1) / (x–2) = 3

General forms for rational expressions:
(2x+1) / (x–2) = 3

First you have to cross multiply the equation
2x+1 = 3(x–2)
Simplify the equation
2x+1 = 3x–6
Isolate for x;

3x–2x = 1 + 6
x = 7.

General forms for Polynomial equations:
x² + 4x – 5 = 0

Factorize the polynomial
x² + 4x – 5 = (x+5)(x–1) = 0
Set each factor equivalent to zero
x+5 = 0, or x–1 = 0
Solve for x, making x the subject of the formula:

x = —5 or 1.

Task 2

Explain steps used in simplifying a rational expression. Write some common factors required to be cancel out?

Factoring of numerator and denominator

This is the first step in simplifying a rational expression. Here, both the numerator and the denominator is factorized in their prime factors.

Cancellation of common factors

This is the second steps. It involve cancelling common factors in between numerator and denominator. For example: 3(x+6) / (x+6) = 4
The common factors is (x+6). And if it is cancelled out, what is left is 3 = 4.

Writing of simplified expression:

At this points, the simplified expression is written out.

Factors required to be cancel are:

Common factors such as:
2(x+2) / (x+2) = 2
The common factor (x+2) can be cancelled out.
After cancelling, this is what we have:
2 = 2.

Task 3

3x² + 2x + 1

Factorize
(3x–1)(x+1) = 0
Set each factor equivalent to zero
3x–1=0 or x+1=0
Solve for x
x = ⅓ or x = –1

2x²–x–3

Factorize
(2x+3)(x–1)
Set each factor equivalent to zero
2x+3=0 or x–1=0
x=–3/2 or 1

Task 4

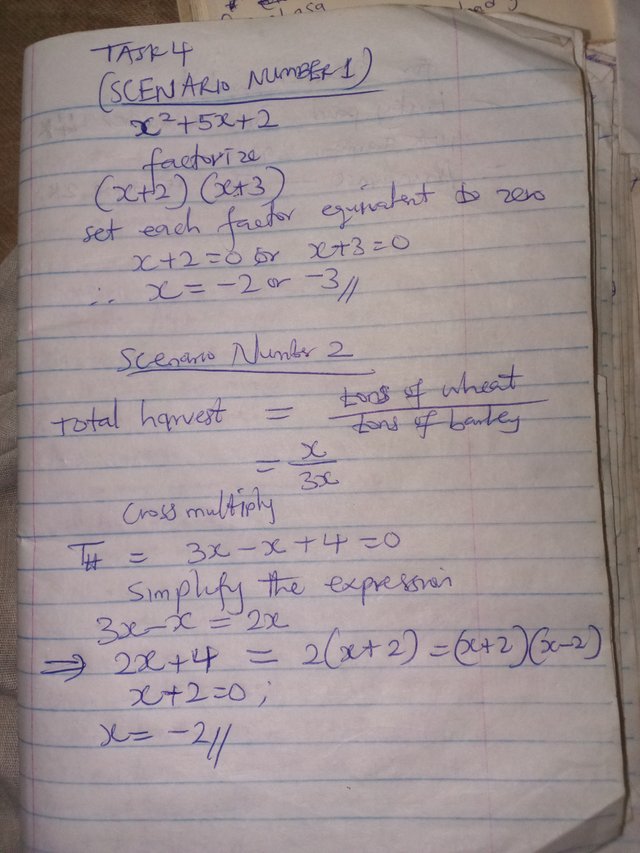
Scenario number 1:

x²+5x+2
Factorize
(x+2)(x+3)
Set each factor equivalent to zero
x+2=0 or x+3=0
Therefore, x=–2 or –3

Scenario number 2:

Total harvest (tH) = tons of wheat / tons of barley
= x/3x
Cross multiply
tH = 3x–x+4=0
Simplify the above expression of tH
3x–x=2x
This implies that; 2x+4 = 2(x+2) = (x+2)(x+2) = 0

x+2 = 0
Therefore, the value of x = –2.

I invite @bossj23, @basil20 and @ngoenyi to participate

#algebra-s22w5 #learningchallenge #steemexclusive #learnwithsteem #nigeria #club100