SLC21 Week4 - Recursia
 |
|---|
Describe recursion as you understand it. Have you encountered recursion before? How is the word "fractal" related to recursion?
According to my understanding, Recursion is a concept in mathematics and computer science where a function calls itself in its definition, frequently with a simpler or smaller version of the original problem. This process we are talking about here continues many times until it reaches a base case, which is a condition that stops (pause) the recursion to prevent infinite loops from occurring.
Recursion was something that I encountered during my second year in school when I was taught about factorial operations, geometric sequences, and arithmetic sequences. In school, I learned that it is a fundamental concept that is used in algorithms such as sorting, for example, MergeSort, and QuickSort. An example is calculating the factorial number:
n! = n × (n - 1)!
From the above, the function factorial(n) calls itself until it reaches the base case n = 0 where 0! = 1
Relationship Between Fractals and Recursion
In terms of fractals, they are geometric shapes that exhibit self-similarity, which means their structure repeats often on different scales. The self-similarity is inherently recursive since the process of creating a fractal involves the repeating of a pattern at progressively smaller scales. A perfect example is the Sierpiński triangle which is built by repeatedly removing smaller triangles from a larger (bigger) triangle, which is a recursive process.
In conclusion, fractals and recursion are closely interrelated because both involve self-repetition at different scales. Recursion is the underlying process that can produce the structure of fractals while fractals are seen as the visual representation of recursion.
Explore the limit of what is the largest value of the factorial that can be calculated with a certain type of data. You should have a table like this
We will need to account for the limits imposed by each type's range if we want to explore the largest factorial that can be calculated for different types. We will need to follow the outline below.
Determine the maximum value for each data type example,
char, int, long, floatetc.Iteratively calculate factorials until the result exceeds the data type's maximum value.
We then need to record the largest
nfor whichn!fits within the type's limit.
We will have to prepare a table structure to include the tg type, the largest n, and the corresponding fractional (n!). Talking about preparing a table, below is the table that we need to prepare.
| Type | Largest n | n! |
|---|---|---|
char | 5 | 120 |
unsigned char | 5 | 120 |
int | 12 | 479,001,600 |
unsigned int | 12 | 479,001,600 |
long | 20 | 2,432,902,008,176,640,000 |
unsigned long | 20 | 2,432,902,008,176,640,000 |
float | 34 | ~2.95 × 10³⁸ |
double | 170 | ~7.26 × 10³⁰⁷ |
From the above table, smaller integer types
char, andunsigned charonly support up to5!.The standard integers, 'int
, andlong` can handle larger factorials but are vastly exceeded as factorials grow rapidly.The floating-point types;
float, anddoublesupport much larger ranges withdoublebeing able to calculate the factorials for up to 170 before exceeding its limits.
Investigate how many calls the function will make before terminating. More details about this task are described in the lecture.
For me to investigate how many calls the function will make before terminating, I will need to analyze the recursion depth for a given problem. However, doing this will depend on the base case and how the input is reduced at each step which below is a common scenario for factorial computation using recursion.
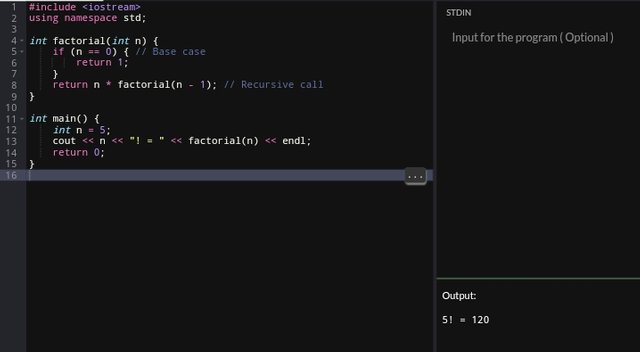
From the above, the number of cells each recursion call reduces n by 1 until n = 0 which is the base case. For the total calls, for input n the function makes n + 1 calls including the base case.
Based on what was described in the lecture, the recursive factorial function illustrated makes a recursive call until the base case n == 0 is reached, which if we change the base case to another condition for example, n <= 1 it could slightly reduce or decrease the number of calls.
Print numbers from 1 to n.
Here I have shared a recursive function to print numbers from 1 to n which can be seen below.
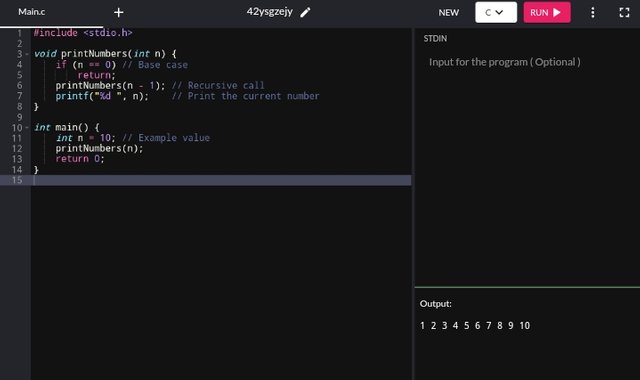
Interpretation
- The base case is
n == 0, where the recursion stops. - The function first makes a recursive call
print numbers (n - 1), which makes sure that all smallest numbers are printed first before the currentn. After tg recursion,printf("%d ", n)prints the number in increasing order.
Print numbers from n to 1.
Here I have shared a recursive function to print numbers from n to 1 which can be seen below.
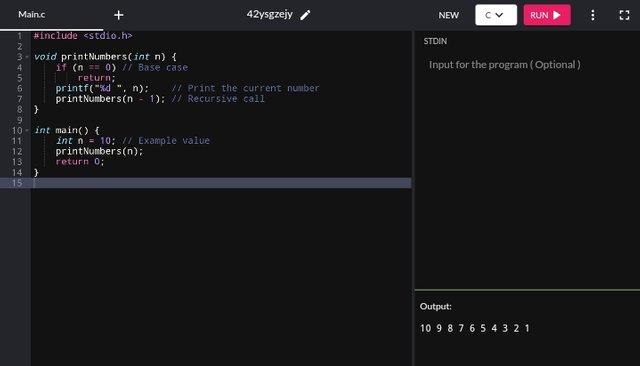
Interpretation
- The base case is
n == 0, where the recursion stops. - The current number
nis printed first (print ("%d ", n)), making sure that the larger numbers are printed before making recursive calls. The function then recursively calls itself withn-1.
Write a function to calculate the sum of two numbers a+b. Do not use the a+b calculation directly. First, perform this task using a loop (1 point), maybe it will tell you how to use recursion here and perform this task (1 point)
For us to calculate the sum of two numbers a+b without using the + operator, we will have to simulate addition through repeated increment and decrementation using a loop or recursion.
Using Loop
By using a loop we can repeatedly increment one number and decrement the other number until the second number becomes zero.
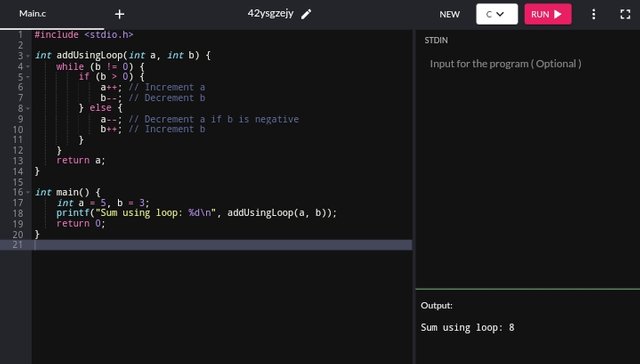
- If b > 0, repeatedly increment
aand decrementb. - If b < 0, repeatedly decrement
aand incrementbwhich stimulates addition operation.
Using Recursion
By using recursion which works similarly to that of the loop, we can reduce the problem in each call by either incrementing or decrementing until b = 0.
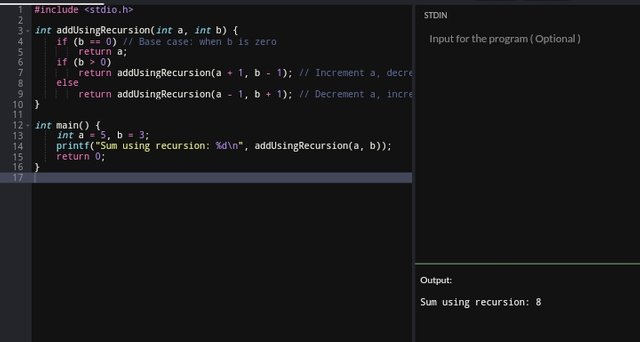
- The function reduces
bin each step by either incrementing or decrementinga. - The recursion stops when
bbecomes zero.
Print a string character by character (as an array). Remember that when declaring a line char s[]="recursia"; sit is not the string itself - it is the address of its first character, the address of the array. And sit is possible to display a character by the address stored in it like this print ("%c", s[0]); or print ("%c", *s);- if sit is the address of an array of characters (line), then s[0]it is its first character. And writing means to dereference the pointer - that is s, to get the value placed at the address. For those who know C++ - it's easier here - just output through couture I will add one more hint: if the address of the first character is the address of the second)))s[0]sss+1
Here I have created a program that prints a string character by character in C, which we can use as a loop or recursion. The string is stored as an array of characters, and each character can be accessed by dereferencing its address or using array indexing.
Using a Loop
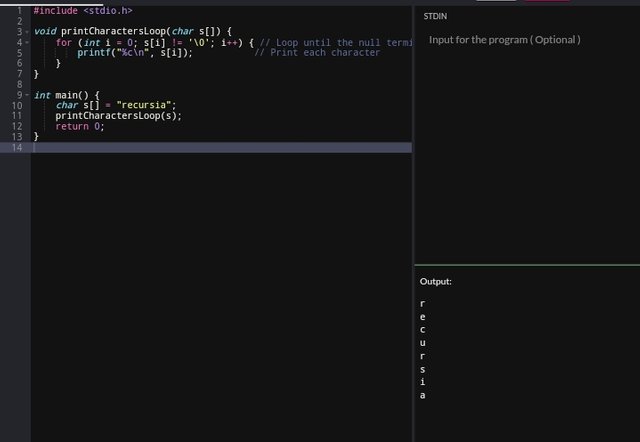
The loop approach iterates over the string, accessing each character using its index s[I] until it reaches the null terminator (0).
Using Recursive
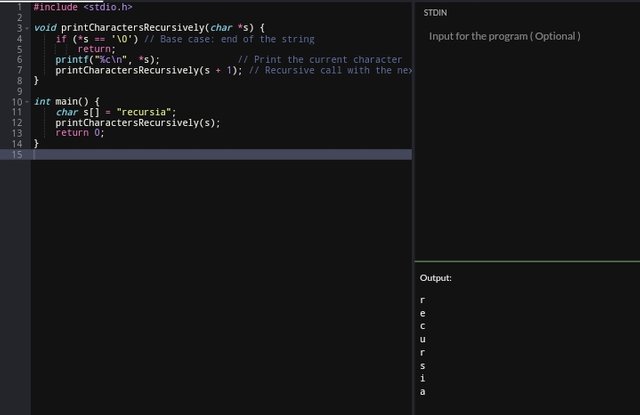
In this approach, the tg function printCharactersRecursively dereferences the pointer *s to access the current character.
Similar to the previous task - but the line must be displayed backward, turned around.
To display a string backward, we can either use recursion to traverse the string until the null terminator 0 and then print the characters during the unwinding of the recursion or we can use a loop to start from the end of the string and move to the beginning.
Using Recursion
This is the approach that first traverses the string to its end and then prints each character while backtracking.
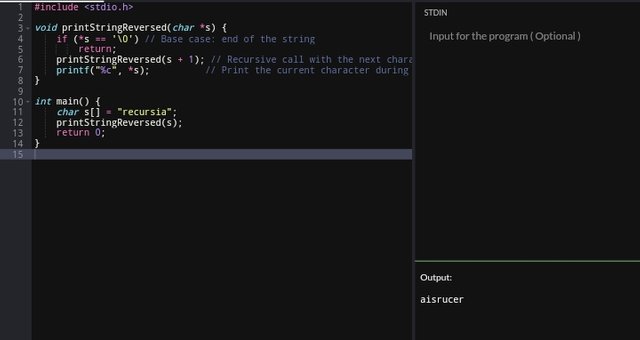
Each recursive call moves the pointer to the next character (s + 1). Also, characters are printed during the backtracking phase, resulting in reversed output.
Using Loop
This is the approach that calculates the length of the string and then Iterates from the last character to the first.
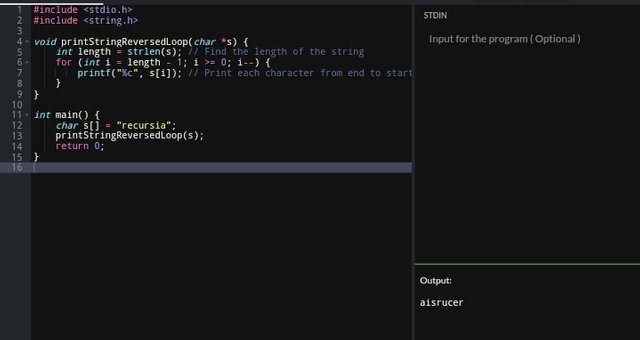
Each iteration prints the current character and moves backward until the first character is reached.
I am inviting; @dove11, @simonmwigwe, and @ruthjoe
Cc:-
@sergeyk
I must actually confess that I was really able to pick a whole lot of new things to learn from your post