SLC-S22W3//Equations and Systems of equations

Hello all Steemian around the world. I hope you are healthy and full of blessing Today I want to join in the lesson with a great teacher. He has given us an important subject. It is about algebra, we call aljabar. The name of aljabar is come from an Islamic scientist who has found the concept of counting using variables.

Now we have been taught a material about equations and systems of equations. The teacher has given us homework. And when we have to answer and then collect it. Here is the homework given and my answer.

Task 1

Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.

There are some differences between linear and non-linear equations. I want to show you about it by a table below.

Linear Equation	Non Linear Equation
1. Use variables with powers of 1 only, the variable exponent is only 1	1. Use variables with powers of more than 1, the variable exponent more than 1
2. If depicted in the form of a graph will show a straight line	2. Will form a curve
3. In their solution only produce one result	3. Have more than one result
4. General form of linear equationsY = mx + c, where x and y are variables, m is the gradient/slope of the line and c is a constant	4. It can be ax2 + bx + c = 0

Now we can see the example linear equation:

1. 2x = 30
2. 3x + 4y +12 = 0
3. x = 2y
4. 2x + 3y = 6

Here the example of Non linear equation :

1. x² + y ² = 4
2. x² + 4x + 3 = 0
3. x² + 12xy + y² = 0
4. x = y²

For practical example of linear equation

• calculate the length of a rectangle if the circumference and width are known
• calculate the amount of fuel needed
• calculate the time needed for a job
• calculate the price of goods if the combination of two goods in different quantities is known
• calculate distance, speed and travel time

For practical example of non- linear equation

• calculate the trajectory of a ball kicked upwards
• calculate the maximum capacity of a gutter made from a sheet of sem
• predict the response of materials to pressure and load

Task 2

Describe any one method for solving system of linear equations and share atleast one step by step algebric example.

(It should be other than substitution, elimination and graphing method)

My answer:

Before I explain about how to calculate linear equation with other way I must explain this first.
Take an example there are linear equations ax + by = m and cx + dy = n.
Now we need to change into an equivalent equation.
For example, if we take the equation ax + by = m, then:
=> ax + by = m
=> ax = m – by
=> x = (m – by)/a
After that we substitute x = (m – by)/a into the other equation, i choose cx + dy = n, and then:
=> cx + dy = n
=> c((m – by)/a) + dy = n
=> mc/a – cby/a + dy = n
=> mc/a – cby/a + ady/a = n
=> mc –bcy + ady = an
=>ady – bcy = an –mc
=> y(ad – bc) = an –mc
=> y = (an – mc)/(ad – bc)

So, we can get value of y

Now we can describe it in the picture below.

Value of y can be determined by multiplying a by n then subtracting m times c, the result of the subtraction is then divided by a times d minus b times c.

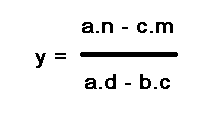
Let's see the example for making easy this method to solve linear equation

1. 3x +2 y = 12 dan –x + 2y = 4
   We will arrange it first so that it is easy to do it quickly, namely:

3x + 2y = 12
–x + 2y = 4

We know that
a = 3, b = 2 , m = 12 and
c = -1, d= 2, n = 4

We enter the formula

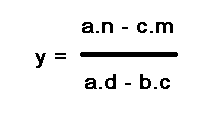
=> y = (3.4 – 12.( –1))/(3.2 – 1 .( –2))
=> y = (12 + 12)/(6 + 2)
=> y = 24/8
=> y = 3

Now substitute y = 3 into one of these equations, for example the equation 3x + 2y = 12, then:
=> 3x + 2y = 12
=> 3x + 6 = 12
=> 3x = 6
=> x = 2
So, the set of solution is {2, 3}.

Task 3

You need for solving following system of linear equations:

(a)

x + 2y = 7
3x - 2y = 5

(b)

4x + 6y = 2
x - 2y = 3

Here my answer.

Task 4

Scenario number 1

Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then;

2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)

If company wants for producing 50 units of product A then calculate how much units of product B they may produce?

(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)

And my answer

Scenario number 2

Suppose there's a bakery producing two types of cakes which are vanilla and chocolate.If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then;

x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)

If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce?

Here my answer

That all my homework. Thank you my teacher @khursheedanwar. I understand a little abut your lesson this time.

That all my writing today. Thank you for stopping by and reading my post. I hope you enjoy it.
Warm regard from Indonesia
@rokhani