(고등수학) 원의 방정식(2)
⦁ 원의 방정식
㈎ 원과 만나는 접선의 방정식
㉠ 접점의 위치를 알 때
㉡ 접선의 기울기를 알 때
이번 포스팅에서는 접선의 방정식을 접선의 기울기를 알 때 구하는 방법에 대해서 알아보도록 하자.
원과 만나는 접선의 방정식을 알고자 할 때 접선의 기울기를 안다면 어떤 방법으로
접선의 방정식을 구할수 있을지 생각해보자.
직선의 방정식 = y = mx + b
원의 방정식 = (x-a)²+(y-b)²=r²
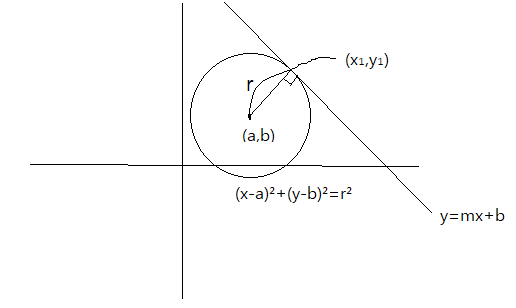
원과 접선을 수직선 위에 그려보고 원의 중점을 (a,b) 접점의 위치를 ( x₁, y₁)으로 하고 그린 그림
접점의 위치는 모르며 기울기 m과 원의 중점은 알고 있을 때 접선의 방정식은 어떻게 구할까
y=mx+b 에서 b의 값을 구하는 것이 관건이다.
생각해보자. 어떻게하면 b의 값을 구할 수 있을까?
우리가 앞서 보았던 원과 직선의 위치관계에서 힌트를 얻을 수 있다.
원과 직선이 접한다는 점과 원과 직선이 접할 때는 그 관계 값을 범위 값이 아니고 등호를 사용하여 D=0 또는 d=r의 형태로 등호를 사용한다는 점에 착안하여 앞서 보았던 원과 직선의 위치관계에서 접선의 위치를 구하는 법을 이용하면 b의 값을 알수 있을 것이다. cf) 여기서 소문자 d는 원과 직선사이의 거리이고 대문자 D는 판별식의 D이며 r은 반지름의 길이이다.
판별식을 이용하여 구해보자
판별식 = b²-4ac
우선 원의 방정식에 직선의 방정식을 대입하여 원과 직선의 위치 관계를 구할때 처럼 이차방정식을 만들어 준다.
기본적인 방법을 보여주기 위해 원의 방정식의 기본형과 직선의 방정식의 기본형을 이용해 나타내 본다.
x²+y²=r²에 y=mx+b를 대입한다. x²+(mx+b)²=r² 이 된다.
이 값을 풀어주면 x²+m²x²+2mbx+b²=r² 이 된다.
x에 대한 이차방정식 형태로 간단히 하면 (1+m²)x²+2mbx+b²-r²=0 이 된다.
이차방정식 형태이므로 판별식을 이용해 본다.
b의 위치가 짝수이므로 b′형태를 이용해 본다.
(mb)²-(1+m²)(b²-r²)의 판별식 형태가 되고 원과 직선의 관계에서 접선의 위치관계이므로 (mb)²-(1+m²)(b²-r²)=0 이 된다. 이걸 풀어주면
m²b²-(b²-r²+m²b²-m²r²)=0 이 된다. 괄호를 풀어주면
m²b²-b²+r²-m²b²+m²r²=0 이 되며 다시 간단히 하면
-b²+r²+m²r²=0 이 된다. b의 값을 구하기 위해 r²+m²r²을 이항해주면
-b² = -r²-m²r² 이 되고 b² = r²+m²r²의 형태가 된다.
b² = r²(1+m²)
b = ±r√1+m² 의 형태가 되며 b의 값을 구할 수 있다.
원과 직선의 길이 d=r 으로도 구할 수 있다.
원과 직선의 길이에서 구할 때는 접점의 위치와 직선의 방정식이 필요하다.
cf) 점과 직선사이의 길이를 참고
하지만 여기서 있는 건 접점의 위치가 아닌 기울기와 원의 중심 그리고 반지름의 길이이다.
어떻게하면 원과 직선의 길이관계로 구할수 있을까
d = | ax₁ + by₁ + c | / √a²+b² 여기서 abc는 직선의 방정식 ax+by+c에서의 abc이고
여기선 원과 직선사이의 거리이므로 x₁과 y₁은 원의 중점의 위치를 나타낸다.
점의 위치와 직선의 방정식을 이용하여 구하는 것이다.
y = mx + b 이므로 mx -y -b = 0 의 일차방정식 형태라고 했을 때
이렇게 되면 m = a, -1 = b, -b = c 의 형태가 된다. 먼저 d를 구해보자
d = | mx₁ -y₁ -b | / √m²+1 이며 반지름의 길이와 같으므로
| mx₁ -y₁ -b | / √m²+1 = r 이 된다. 이 식을 풀어보면
| mx₁ -y₁ -b | = r√m²+1 이 되고 mx₁ -y₁ -b = ±r√m²+1 이 된다.
b = -x₁ +y₁ ±r√m²+1 이라는 식이 도출 되게 된다.
원과 접선의 기울기를 알 때 접선의 방정식을 구하는 방법을 알아보고 식을 도출해 보았다.
(본 글의 수정되어야할 부분은 알려주신다면 수정하겠습니다.)
Congratulations @vhzhxls! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honnor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBy upvoting this notification, you can help all Steemit users. Learn how here!
이 공식 정말 오랜만에 보는데요... 그때도 어려웠지만 지금은 더 어렵네요 ㅠ 가끔씩 머리 식힐겸 보야곘습니다 ㅎㅎ 좋은 포스팅 감사합니다 :)
좋은 댓글에 저도 감사드립니다^^
ㅠㅠ; 가슴 아픈 말이지만 솔직히 말씀드리겠습니다
이런 글은 인기가 없을거 같아요.
물론 이것도 하나의 개성이지만
여기 있는 '한국' 사람들은 수학에 대해서 별로 좋은 기억이 없는
사람들 일 것입니다.
방정식이 있고 해를 구하는 것은 수도 없이 해봤겠죠
하지만 그건 공부라기보다 대학을 위해서 하는 노가다 측이었을 겁니다
그렇다면 이런 곳에선
방정식과 그의 풀이 방법보다는
왜 방정식이란게 나왔는가.. 옛사람은 이걸 무엇때문에 만들었는가
이런 얘기를 풀어서 해주시던가
아니면 이 수학능력으로 여기의 높은 관심을 받고 있는 코인에다가 적용해보는건 어떨까 합니다
그것도 아니면 놀이공원들의 놀이기구들은 사실상 수학의
결정체라고 하던데 어디에 어떻게 적용되며 잘못되면 어떤 일이 벌어지는가
이런거면 흥미진진 할 거 같습니다
물론 그대로 쭈욱 밀고나가서 하나의 브랜드를 만드는 방법도 있긴합니다만 그 경우는 좀 고생하실거 같아서 말씀드립니다
솔직한 말씀 감사합니다 그냥 하는 말이 아니고 진심입니다^^
이 글이 코인에 관련한 글 혹은 다른 글보다도 관심을 끌기 힘들 수도 있다는 것을 저도 알고는 있습니다. 코인에 관련된 글은 인기가 있겠지만 일부러 쓰지 않았습니다. 이미 많은 정보가 올라와 있기 때문입니다. (코인에 대한 글을 쓰시는 분들이 관심을 끌기위해 글을 쓴다는 것은 아닙니다. 정보공유를 위해 쓰시는 것이겠지요. 그것도 매우 좋은 일이라고 생각합니다.) 저는 인기와는 무관하게 사실 읽을 필요성을 느끼지 못할지도 모르는 그런 글을 조금 지루하고 흥미를 끌기 힘들 수 있는 있는 그런 글을 그저 글을 쓴다는 거에만 초점을 맞춰 쓰려합니다. 인기의 여부 보다는 그저 쓰고자하기 때문에 스팀에 글을 쓰려합니다. (간혹 달리는 댓글을 읽는 재미도 있고요 ㅎㅎ) 그러다 다른 글을 쓰고 싶게되면 다른글을 쓸지 모르겠습니다. 사실 제 글이 흥미를 끌지 못하는 건 글의 주제도 주제이지만 글의 수준이 낮아서이기도 할 겁니다. 그 부분에 대해서는 변명의 여지가 없습니다. 저를 걱정해주신 글에 괜히 뜨끔해서 변명하는 거 같네요. 이렇게 댓글을 남겨주셔서 진심으로 감사드립니다.
부가적으로 간혹 고등수학같은것을 검색하다가 스팀에 들어오시는 분들에게 발판이 되어드릴수도 있지 않나 생각해봅니다^^
수학의 응용분야 수학이 어떻게 쓰이는가 그런 것들을 알면 수학에 대한 흥미를 높일 수 있을거 같긴 합니다만 저는 수학에 관한 분야에 쓰는 것이 아니라 고등수학 혹은 중등수학에 대해서 쓰고자 합니다. 수학과 관련된 흥미로운 주제에 관한 제안은 유용한 제안 같고 나중에 쓸 수도 있겠네요. 참고하도록 하겠습니다.
재미있게 읽는 저 같은 사람도 있어요 ㅎ @vhzhxls님! 다른 글들도 기다리고 있을게요~