Excellent Modification Of Breadth First Search
I have started with graph theory problems on http://acm.timus.ru/ . Solving problems here has certain advantages according me. If you have familiarity with basic graph algorithms like BFS,DFS,Dijkstra,Prims, you will almost immediately recognize their application to a problem. But you have to modify the algorithms to great extent to solve the problem. So basically it gives me opportunity to test and upgrade my knowledge of algorithms.
I recently encountered a problem . http://acm.timus.ru/problem.aspx?space=1&num=1930 . I will like to discuss the problem and my approach to solve the problem.
Problem is to reach from city A to city B by a car with many cities in between. The roads between cities have slope. On either road we can go either uphill or downhill. But we have to change gear of car if we were first going uphill and now we have to go downhill or vice versa. In starting we can choose any gear mode ( uphill or downhill) . We have to find minimum number of gear changes to reach from city A to city B.
My first thought was to apply BFS and find out the minimum distance from city A to city B . But soon I realized that a shorter path can have more number of gear changes than a longer path with less number of gear changes.
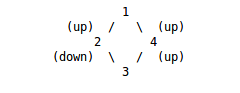
Figure above shows a simple graph. 1 is our start vertex and 3 is our final vertex . I start BFS from vertex 1 and add its two neighbours 2 and 4 to queue. After that we take 2 and add its neighbours(unvisited) to queue . Here 3 is the only neighbour of 2. So we add it to queue. In this way we can reach 3 by one gear change. But what if we start from 1 and 4 to queue first and then 2. Then we take out 4 from queue and reach 3. In this way we reach 3 with zero gear change.
So suppose I do BFS and mark a vertex(city) as visited only to realise later that I could have reached that vertex with fewer number of gear changes. So I tried to modify my BFS . I decided to visit a vertex even though it is visited.(An approach similar to Dijkstra).
I took three containers slope ( To store whether edge from city u to v is uphill or downhill) , howArrived( To store whether I arrived at a vertex by downhill slope or uphill ) , gearChanges ( To store number of gear changes I have done when I reach a vertex).
In BFS , suppose I reach vertex v from vertex u. There are two cases :-
If vertex v is not visited :- We see the slope of edge u->v and update howArrived accordingly. If slope of edge u->v is downHill (0) then howArrived[v]=0 and if slope of edge u->v is upHill(1) then howArrived[v]=1 . Also if howArrived[u] is different than howArrived[v] it means we had to change gear to reach from u to v. Thus we update gearChanges[v]=gearChanges[u]+1. Otherwise gearChanges[v]=gearChanges[u].
If vertex v is visited :- If slope of edge u->v is different from howArrived[u] it means we had changed gear from u to v. But this time before updating we will check gearChanges[u]. If gearChanges[v]<gearChanges[u]+1 then there is no need to update . Otherwise gearChanges[v]=gearChanges[u]+1 . If slope of edge u->v is same as howArrived[u] it means we did not change gear to come from u to v. If gearChanges[v]<gearChanges[u] then there is no need to update otherwise gearChanges[v]=gearChanges[u]. Also we have to update level of vertex v accordingly.
Here is my code :- http://ideone.com/iLeGnr
This might not be the only way to solve the problem . But I felt so awesome after solving the problem that I felt like sharing it. I originally wrote it on my Quora and Medium blogs.
Congratulations @mayankpratap! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP