How to calculate the perimeter of a square
The perimeter of a two-dimensional geometric shape is the total distance around that shape or the sum of the length of its sides. By definition, a square is a shape of four straight sides of equal length and four angles (90 degrees). Since the four sides have the same length, finding the perimeter of the square will be really simple! This article will show you how to calculate the perimeter of a square if you know the length of a side. Then it will show you the way to find the perimeter of a square if you only know its area and, finally, it will teach you to find the perimeter of a square that is inscribed in a circle with a known radius.
Method 1
Calculate the perimeter when the length of one side is known
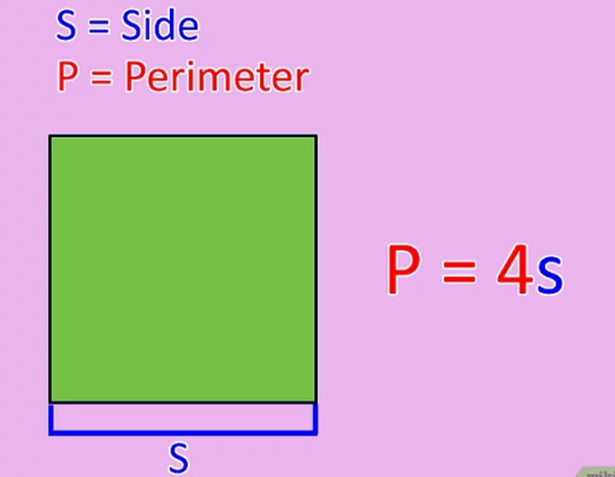
Remember the formula of the perimeter of a square. For a square whose length is L, the perimeter is simply four times the length of the side: P = 4L.
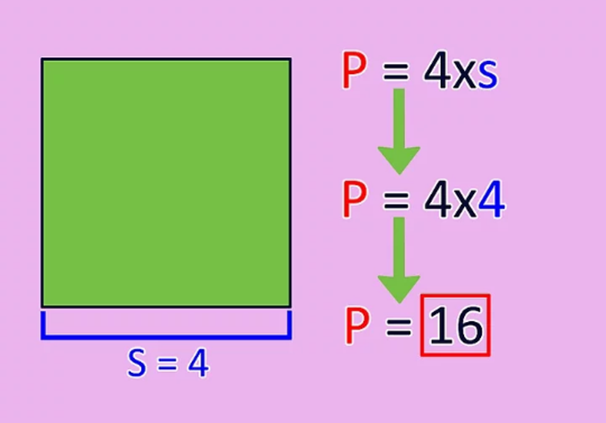
Determine the length of one side and multiply it by 4 to find the perimeter. Depending on what you should do, you may need to measure the side with a ruler or see more information on the page to determine the length of the side. Here are some examples to calculate the perimeter:
- If one side of the square has a length of 4, then P = 4 * 4 or 16.
- If one side of the square has a length of 6, then P = 4 * 6 or 36.
Method 2
Calculate the perimeter when the area is known
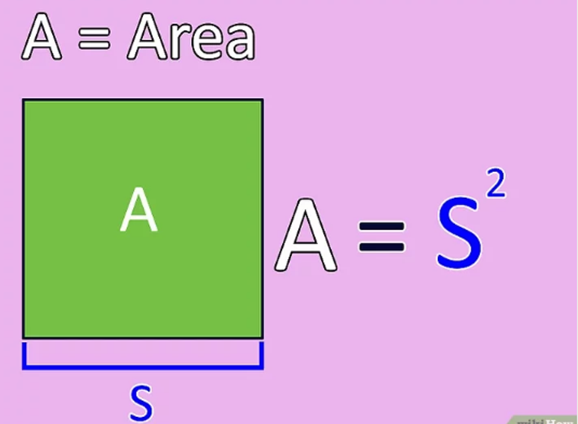
Know the formula for the area of a square. The area of any rectangle (remember, squares are special rectangles) is defined as its base by its height. [3] Since the base and the height of a square have the same length, the area of a square with the same length on all sides L is L * L or A = L2.
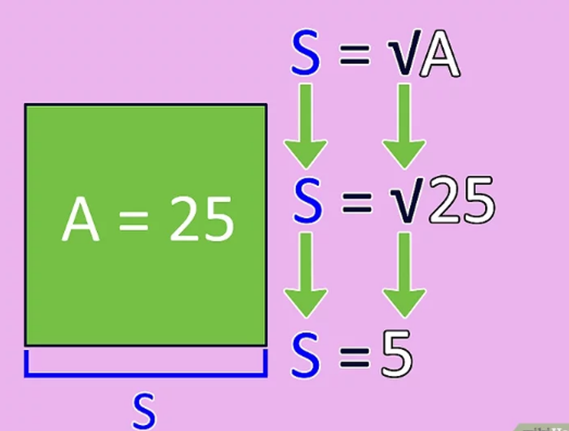
Find the square root of the area. The square root of the area will give you the length of one of the sides of the square. For most numbers, you will need to use a calculator to find the square root by first writing the value of the area, followed by the square root sign (√). You can also learn to calculate a square root by hand!
- If the area of the square is 20, then the length of the side L = √20 or 4.472.
- If the area of the square is 25, then s = √25 or 5.
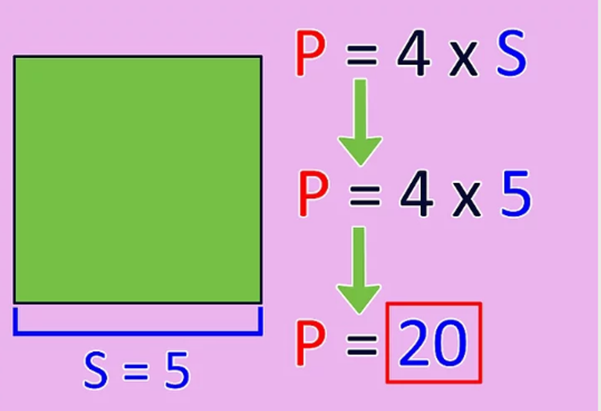
Multiply the length of the side by 4 to find the perimeter. Take the length of the L side you just calculated and connect it to the perimeter formula, P = 4L. The result will be the perimeter of the square!
- For a square with an area of 20 and a side length of 4,472, the perimeter P = 4 * 4,472 or 17,888.
- For a square with an area of 25 and a side length of 5, P = 4 * 5 or 20.
Method 3
Calculate the perimeter of a square inscribed in a circle of known radius
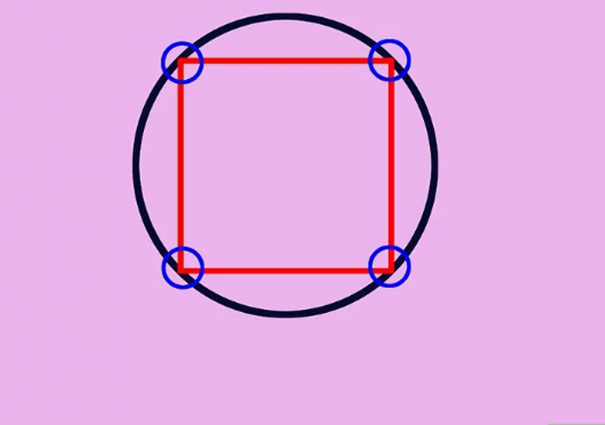
Understand what is an inscribed square. Often, the inscribed forms are easily presented in standardized examples such as GMAT and GRE, so it is important to know what they are. A square inscribed in a circle is a square drawn inside the circle, so that the four vertices (corners) lie at the edge of the circle.
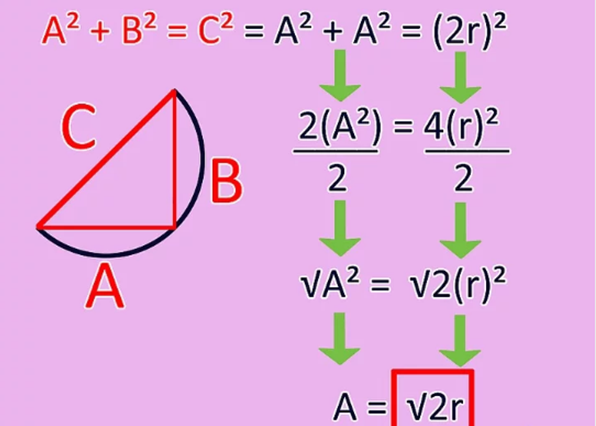
Recognize the relationship between the radius of the circle and the length of the square side. The distance from the center of a square inscribed to each of its corners is equal to the radius of the circle. To find the length of L, we must first imagine that we cut the square in half on the diagonal to form two right triangles. Each of these triangles will have equal sides a and b plus a hypotenuse c, which we know is equal to twice the radius of the circle or 2r.
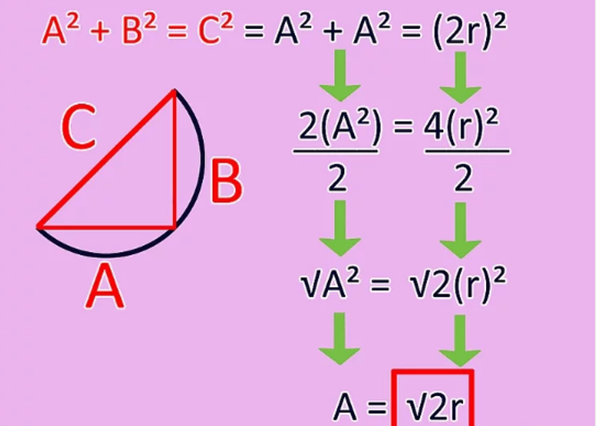
Use the Pythagorean theorem to find the length of the side of the square. The Pythagorean theorem determines that for any right triangle with sides a and b, and a hypotenuse c, a2 + b2 = c2. [5] Since the sides a and b are equal (remember that we are still dealing with a square!) And we know that c = 2r, we can write down the equation and simplify it to find the length of the side in the following way:
- a2 + a2 = (2r) 2 "', now simplify the expressions:
- 2a2 = 4 (r) 2, now divide both sides by 2:
- (a2) = 2 (r) 2, now take the square root of each side:
- a = √ (2r). The length of the side s for the inscribed square = √ (2r).
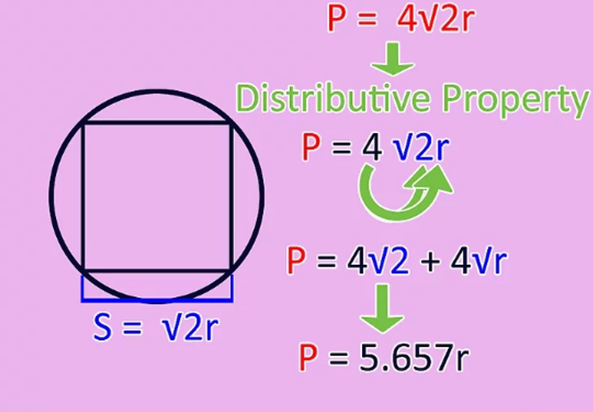
Multiply the length of the square side by four to find the perimeter. In this case, the perimeter of the square P = 4√ (2r). Due to the distributive properties of the exponents, which tells us that 4√ (2r) is equal to 4√2 * 4√r, we can simplify it to the following equation: the perimeter of any square inscribed in a circle with a radius r is defined as P = 5,657r!...
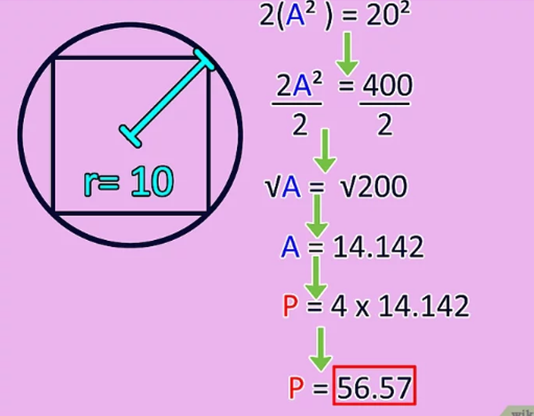
Solve a model equation. Consider a square inscribed in a circle with a radius of 10. That means that the diagonal of this square = 2 (10) or 20. Using the Pythagorean theorem, we know that 2 (a2) = 202, so 2a2 = 400. Now divide both sides in half to find a2 = 200. Then take the square root of each side to find that a = 14.142. Multiply it by 4 and find the perimeter of the square: P = 56.57.
- Keep in mind that you could have found the same by simply multiplying the radius (10) by 5,657. 10 * 5,567 = 56.57, but that might be hard to remember during an exam, so it's best to memorize the process we used in this article to find the answer....