As probably know the people who are reading this post, the so-called Fibonacci succession was introduced by the Italian mathematician Leonardo de Pisa (1170-1241), who was known as Fibonacci, that is, son of Bonaccio, in his book "Liber Abaci" (1202, The Book of the Abacus), as a solution to one of the ingenuity problems that arose in it.

Work "The Fibonacci sequence" by the Venezuelan artist Rafael Araujo

Recall the problem in question:

"Let's consider a family of rabbits with the characteristic that they take a month to be fertile. When they have reached fertility, each pair mates having the next month (each female) a pair of young (a male and a female) that will again take a month to be fertile and then they will mate. How many pairs of rabbits would there be after a given time, for example, a year? "

Number of pairs of rabbits during the first months

It is not difficult to realize that the succession of pairs of rabbits, assuming that they do not die, that there is each month is the following:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

that has the property that each number of the sequence, Fn, is equal to the sum of the two previous numbers, Fn = Fn - 1 + Fn - 2, for n = 1, 2, 3, ...

The succession of Fibonacci is not only interesting within mathematics, but plays a fundamental role in the study of the morphology of plants, specifically, in phylaxis, the number of spirals of the heads of sunflowers, pineapples or the romanescu, numbers of this succession, we also find it in art, as in the works of the Italian artist Mario Merz (1925-2003), or in literature, as in the poem Alphabet (1981) by Danish poet Inger Christensen (1935-2009).

Fibonacci numbers in the Mole Antonelliana building in Turin (Italy), by the artist Mario Merz. Wikimedia (Felpe Cadoná)

However, in this post we will not talk about the mathematical properties of the Fibonacci succession or the presence of this in nature and culture, but we will travel to India, a few centuries before the Italian mathematician Fibonacci wrote his book Liber Abaci, to discover the presence of Fibonacci numbers in poetry in Sanskrit.

In 1985, the Indian mathematician Parmanad Singh, of the Raj Narain College of India, published the article The so-called Fibonacci Numbers in Ancient and Medieval India in the Historia Mathematica magazine (The so-called Fibonacci numbers in ancient and medieval India) , in which he showed the Indian origin of the Fibonacci numbers and their connection to poetry in the Sanskrit language.

In poetry in Sanskrit, the ancient language of India, there are poems in which there is a fixed number of syllables per verse (the so-called varna-vrttas) and those in which there is a fixed number of "blackberries" per verse (called matra-vrattas). For those of us who did not know what the "default" is, this is "the unit that measures the syllabic weight, that is, the duration of the phonological segments that make up the syllable" (according to Wikipedia). In Sanskrit there are two types of syllables, some short (called laghu), one blackberry or syllabic instant, and other long (called guru), two blackberries.

Latin, like the classic Indian languages, Sanskrit and Prakrit, or Greek, also consisted of two types of syllables, short and long. The syllables could have only one default, like those syllables ending in a short vowel, since in Latin there was a distinction between short and long vowels, and those with two blackberries, which were the rest of the syllables, those ending in long vowels or in consonants. . The same word could have two different meanings depending on whether the vowel was short or long, so the "a" of "mălus" was a short vowel and the word meant "bad", while in "mālus" the vowel was long and the meaning was "apple tree", or also "mast". The first word had two syllables with three blackberries, while the second had two syllables with four blackberries. Another example of a word with two meanings depending on whether the vowel is short or long is "solum", with a short vowel "sŏlum" meant "floor", while it had the meaning of "solo" with the long vowel, "sōlum" .

Returning to Sanskrit, a verse of the varna-vrttas type, let us remember that in this type of metric the number of syllables of each verse is maintained, with three syllables it has 8 possibilities, in relation to the moras that compose it. If we call C a short syllable, with a blackberry, and L a long syllable, with two blackberries, the possible structures, in relation to the blackberries, are 8: CCC, LCC, CLC, CCL, CLL, LCL, LLC and LLL. Although the number of syllables remains constant, the number of blackberries varies from one structure to another, the first has 3 blackberries, the next three blackberries, the three with two long syllables have 5 blackberries and the last has 6 blackberries.

However, if we consider a verse of the matra-vrttas type, let us remember that in this type of metric the number of blackberries of each verse is maintained, with three blackberries, there are only 3 possible structures CCC, CL and LC, the variable now being number of syllables, the first with three syllables and the others with two.

But ... what do poems in Sanskrit have to do with Fibonacci numbers?

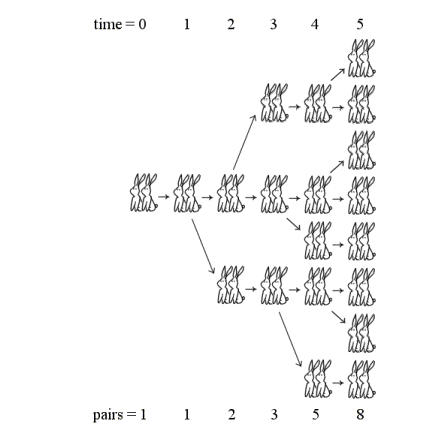
To answer this question, let's focus on the matra-vrttas metric. Let's see how many possible structures exist of verses with 1, 2, 3, 4 or 5 blackberries.

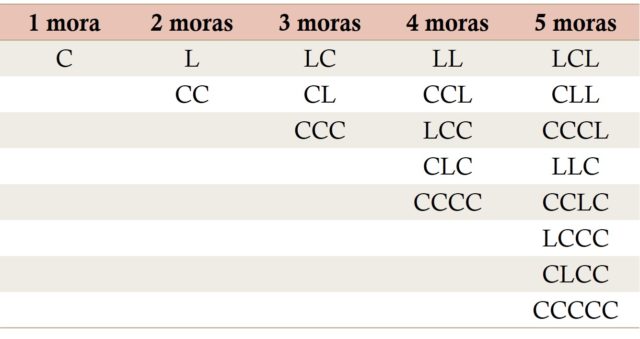
The number of possible variations, for verses with 1, 2, 3, 4 or 5 blackberries, are 1, 2, 3, 5 and 8, which as we can see are Fibonacci numbers. But let's look, for example, at the structures of the verses with 4 blackberries, we can divide them into two types, those that end in a long syllable (L), which are the two structures with 2 blackberries (L and CC) to which two blackberries have been added by a long syllable (LL and CCL), and those ending in a short syllable (C), which are the three structures with 3 blackberries (LC, CL and CCC) to which a delay has been added using a short syllable (LCC, CLC and CCCC). Consequently, there are 2 + 3 = 5 possible structures with 4 blackberries.

If now we would like to see how many different structures exist for the verses of the matra-vrttas metric with 6 blackberries, we will get that they are 13, those generated from the 4 blackberries by adding a long syllable (L), which are 5, and the generated from those of 5 berries by adding a short syllable (C), which are 8, then in total 5 + 8 = 13. In particular, LLL, CCLL, LCCL, CLCL and CCCCL, along with LCLC, CLLC, CCCLC , LLCC, CCLCC, LCCCC, CLCCC and.

Therefore, what we are saying is that the number of possible structures with m is equal to the sum of the number of structures with m - 1 and m - 2 mora, which is the reason why the Fibonacci numbers come out. In summary,

The number of possible structures for matra-vrtta verses with mrras is equal to the Fibonacci number Fm + 1 !!

If we take into account that a short syllable (C) is 1 time and a long syllable (L) is 2 times, we can write the previous result as a mathematical result.

Theorem: The Fibonacci number Fm + 1 is equal to the number of ways to obtain the number m as sums of 1s and 2s, where the order does matter.

For example, above we have seen that the number 4 can be obtained as five different sums with 1s and 2s, namely 2 + 2, 1 + 1 + 2, 2 + 1 + 1, 1 + 2 + 1 and 1 + 1 + 1 + 1, following the order of the previous table.

We have already seen the relationship that poetry in Sanskrit has with the Fibonacci numbers, but the question now is whether in India they were aware of this relationship. Let's see what Parmanand Singh tells us in his article.

According to this author, Acarya Pingala (who lived between 700 a.c. and 100 a.c.), who was the first authority in the study of metrics in India, could have knowledge of these numbers, known as Fibonacci numbers. However, there is no direct evidence of this, but in the comments of his work made in the tenth century by the commentator Yadava, this speaks of the rule of Pingala "misrau ca" (something like "and the two together" ) to explain the expansion of the matra-vrttas by combining the expansions of the two previous metrics by adding a guru (L) and a laghu (C), respectively. And something similar happens with another ancient authority in the metric of India, Acarya Bharata, who could live between 100 a.c. and 350 d.c.

However, the first authority in the study of metrics in India that explicitly mentions the rule of the formation of the numbers of variations of matra-vrttas was Acarya Virahanka, who lived between the sixth and eighth centuries. You can read something like this in one of his works "Putting together the variations of the two previous metrics, you get the amount. This is a method to know the number (of variations) of the next matra-vrtta. "

And the first author who explicitly mentions the Fibonacci numbers, while analyzing and commenting on the work of Acarya Virahanka, is Gopala, whose manuscript commentary on the work of the previous one is dated between 1133 and 1135.

Another authority that explicitly mentions the rule of the creation of the matra-vrttas and the Fibonacci numbers was the poet and scholar of the Acarya Hemacandra metric, in his study on the Chandonusasana metric (1150). Hemacandra's rule can be translated something like this "the sum of the numbers [of variations] of the last and the last, gives rise to that of the next matra-vrtta," and explicitly mentions, as Gopala did, "1, 2, 3, 5, 8, 13, 21, 34 and continue in this way ".

Parmanand Singh mentions another famous work on metrics in which some rules are given on the Fibonacci numbers, Prakrta Paingala, possibly published in the fourteenth century.

All these studies on the metric of the matra-vrttas belong to the field of the science of metrics, but the first mathematical study in India of the Fibonacci succession was the work Ganita Kaumudi (1356) by the mathematician Narayana Pandita, after the work of the Italian mathematician Fibonacci. In this work we study more successions of numbers, in addition to the Fibonacci, as the well-known succession of the cows of Narayana, of which we speak in the entry The cows of Narayana, the Hindu version of the Fibonacci rabbits.

Cartoon of Fibonacci, made by the artist Enrique Morente for the exhibition The Human Face of Mathematics

Bibliography:

1.- Mario Livio, The golden ratio, The history of phi, the most surprising number in the world, Ariel, 2006.

2.- Parmanad Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, History Mathematica 12, n. 3, p. 229-244 (1985).

3.- Website of the artist Rafael Araujo

About the author: Raúl Ibáñez is a professor at the Department of Mathematics of the UPV / EHU and collaborator of the Chair of Scientific Culture