Euclid’s Proposition 1:8
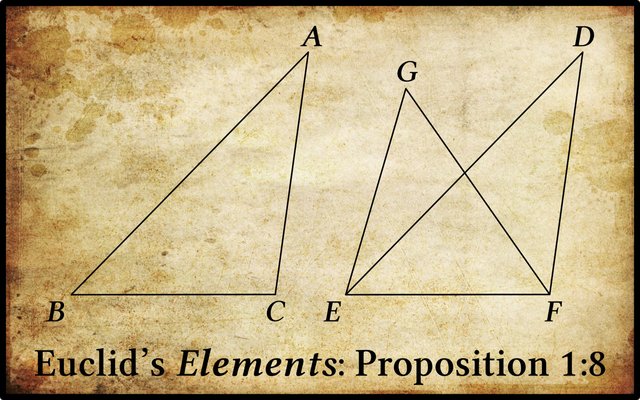
The eighth proposition of Book 1 of Euclid’s Elements is another theorem about triangles:
| Greek | English |
|---|---|
| ᾿Εὰν δύο τρίγωνα τὰς δύο πλευρὰς [ταῖς] δύο πλευραῖς ἴσας ἔχῃ ἑκατέραν ἑκατέρᾳ, ἔχῃ δὲ καὶ τὴν βάσιν τῇ βάσει ἴσην, καὶ τὴν γωνίαν τῇ γωνίᾳ ἴσην ἕξει τὴν ὑπὸ τῶν ἴσων εὐθειῶν περιεχομένην. | If two triangles have two sides equal to two sides, respectively, and also have the base equal to the base, then they will also have equal the angles encompassed by the equal straight-lines. |
This is the Side-Side-Side Congruence Theorem (SSS), the second of Euclid’s three congruence theorems for triangles. Proposition 1:4 gave us the first: the Side-Angle-Side Congruence Theorem (SAS). As was the case for 1:4, Euclid relies upon superposition to prove this theorem. This theorem is a partial converse of 1:4. Euclid only proves that one angle of the first triangle is equal to the corresponding angle of the other triangle. But because each of the sides of the first triangle are equal to the corresponding sides of the second triangle, we can choose any side as our base and use this theorem to prove that the two triangles are congruent. It has also been pointed out by several commentators that once this theorem has been proved, the congruence of the given triangles follows from proposition 1:4, since this theorem establishes a Side-Angle-Side relationship between the two triangles (Heath 262 : Morrow 210).
Euclid relies upon Proposition 1:7 and Common Notion 4 to prove this theorem:
Proposition 1:7 On the same straight-line, two other straight-lines equal, respectively, to two (given) straight-lines (which meet) cannot be constructed (meeting) at a different point on the same side (of the straight-line), but having the same ends as the given straight-lines.
Common Notion 4 And things coinciding with one another are equal to one another. This common notion underpins Euclid’s method of superposition.
In modern terminology Euclid’s proof of this theorem is as follows:

Philo of Byzantium
Euclid uses Proposition 1:7 to prove this theorem, but it can be proved without having recourse to this lemma. As early as the 3rd century before the Common Era the engineer Philo of Byzantium did just this. His proof also relies upon the method of superposition. Its principal drawback is that three cases must be proved separately. Heath gives a clear presentation of this proof (Heath 263–264).
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Oliver Byrne, The First Six Books of The Elements of Euclid in Which Coloured Diagrams and Symbols Are Used Instead of Letters for the Greater Ease of Learners, William Pickering, London (1847)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Volume 1, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
Online Resources
