What is 0 to the power of 0?

Mathematics works or fails based on assumptions or definitions. We can easily make the simple equation of x - 1 = 3 unsolvable by assuming that x is not 4. In this article I want to present you arguments for the definition of 0^0 (0 to the power of 0).

First, we should realize that 0^0 = 0^(0+0) = 0^0 * 0^0. Now we can raise the question which number multiplied by itself is actually itself? Maybe 3 = 3 * 3? No obviously not. However 1 = 1 * 1 is true as well as 0 = 0 * 0 is true. That means we have 3 ways to deal with 0^0.

1. 0^0 = 1
2. 0^0 = 0
3. 0^0 is undefined

1. Is 0^0 = 1?

Let´s first make sure that everybody understands that x^0 = 1 for all x that are not 0.

Please keep in mind that x^a/x^b = x^(a-b).
x^3 = x^3 is obviously true. We can divide by x and get (x^3)/x = x^2. Now we can divide again (x^3)/(x^2) = x and divide by x a last time to get (x^3)/(x^3) = (x^1)/(x^1) = x^(1-1) = x^0. Since (x^3)/(x^3) = 1 we get x^0 = 1. Due to this reasoning we can see that x = 0 is not allowed, because otherwise we would divide by zero. Therefor this reasoning cannot confirm that 0^0 = 1. If you are interested in the problem of dividing by zero feel free to read my article on that topic.

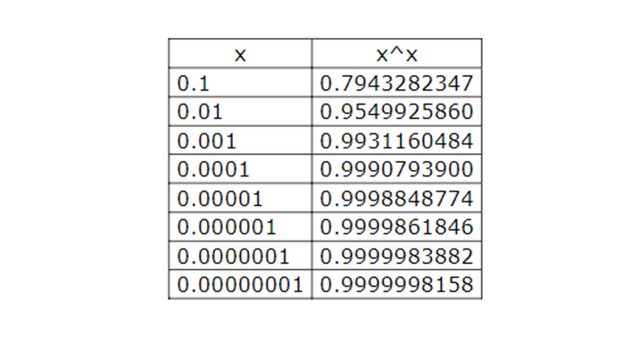
There is an argument that uses a limit. If we take the function x^x and let x get smaller and smaller (that is 2^2, 1^1, 0.7^0.7, 0.1^0.1, 0.001^0.001 and so on) we can observe that x^x approaches 1. We can see this if we look at some numbers.

There is a proof, though. You need to understand a little bit about calculus however. Namely exponential/logarithmic functions and L´Hospital rule. Sketch:

x^x = e^(xln(x)) and with x->0 lim e^(xln(x)) = e^0 = 1.

A plot of x^x:

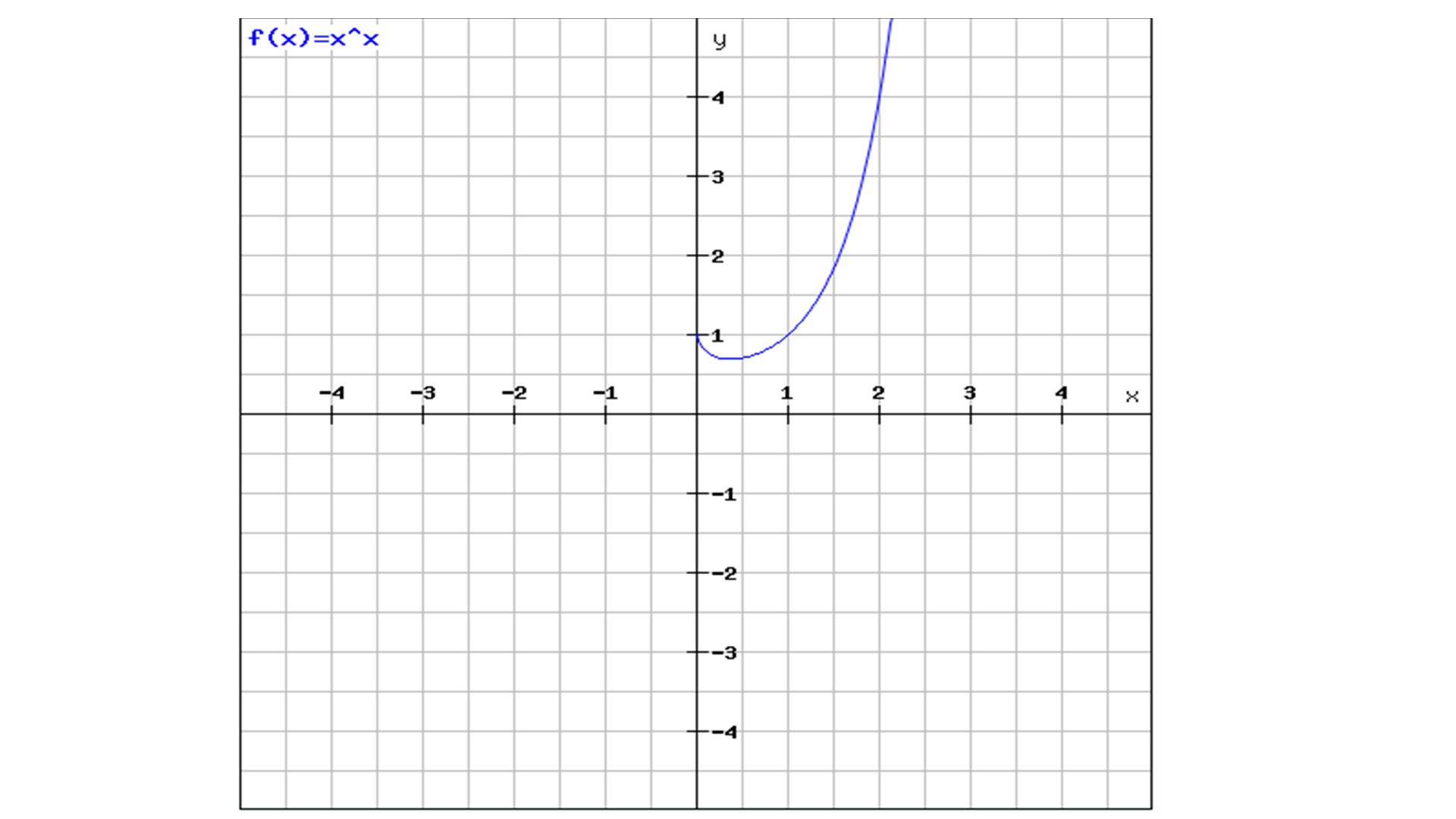
Despite all of this it does not mean that the function f(x) = x^x is defined at x = 0. This limit simply tells us that there is an infinite number of values that are "close" to 1. Limits do not tell us anything about literal equalities.

However, we run into serious problems if we do not allow 0^0 to be equal to 1. Can you spot where 0^0 appears in the following formulas?

Binomial Theorem

Exponential function

Geometric series

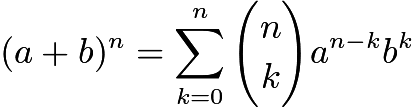
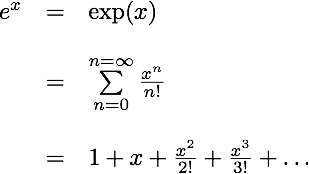
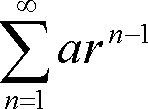
2. Is 0^0 = 0?

Consider the following equation:

0 = 0 * 0 = 0^2 or in general 0 = 0^x if x > 0 (if x < 0 than we divide by zero!). I´ve read several articles on that topic that suggest it is okay to define 0^0 = 0, because if it holds true for 0^x (x > 0) than why should it not be true for 0^x with x being 0? I think this argument is very weak. I can easily flip the question and ask why should it be true? The Bitcoin doesn´t rise, because it has risen in the past - It rises, because demand is higher than supply. The first argument is an argument of induction, the letter an argument of deduction. In mathematics we can only use deductive arguments. I hope you get the analogy.

3. Is 0^0 undefined?

Due to the rigorous style of mathematics a lot of mathematicians agree on 0^0 being undefined. I am personally not sure. We can clearly see that it is useful to set 0^0 = 1 (see formulas above). I think that we have to be very cautious that we do not run into contradictions, though.

In summary there is no convincing argument for any of the 3 possibilities. Algebra tells us that 0^0 = 1 doesn´t work, calculus tells us it is a limit however. 0^0 = 0 is utter speculation in my opinion and not defining 0^0 at all causes trouble. Therefor I agree with the guys who think that it should be undefined and only be defined as 0^0 = 1 in certain circumstances. What do you think? Do you think 0^0 = 1 should be defined in general? Do you think 0^0 = 0? Should it not be defined at all?

If you find any mistakes please write them in the comments. If you liked this article feel free to upvote and follow. Thanks.

Trivia:

Google calculator tells us it is 1 ;)