The science involved in spinning a body // Movements involved in circular trajectories in petroleum engineering
Introduction
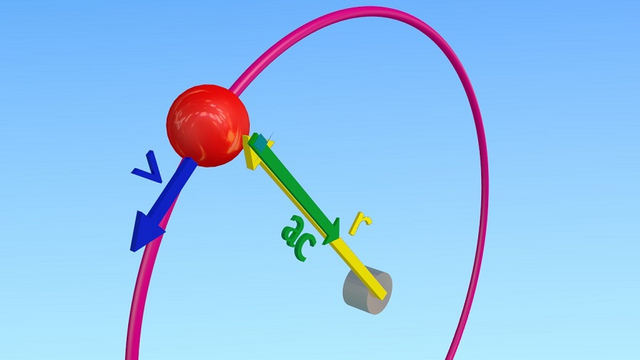
For the case of movement in a plane, we have more categories, since bodies not only perform parabolic trajectories over time. We have the case of circular trajectories, such as the movement that has the wheel of a car, the wheel of a children's park, in any case where there is a circular path.
In real daily life we are also presented with cases in which the movement of a body seems not to have a special trajectory, but if we recognize that it moves in a "going and coming" or "swinging" around an imaginary axis, in a way Periodic as it happens with the movement of a pendulum or the expansion and understanding of a spring and in those cases are called harmonic or oscillatory movements.
It is necessary to keep in mind that all these conditions in which these movements occur occur within the field of action of the gravitational force of the earth, in the case of the rise or fall of the bodies, we will remember that the acceleration that these acquire is the acceleration of gravity, which means that the force that accelerates them is the force of gravity, with which we can conclude then that the acceleration of a body is a consequence of the action of a net force acting on it.
Based on the whole conceptual basis analyzed in the previous paragraphs, I make the following question:
What will be the forces responsible for accelerating a body in circular motion or in periodic movements?
How can we describe the effects caused by these forces?
All concerns can be answered by observing and analyzing the circular movements that occur in nature, if we look at our surroundings, we will realize that the movements in curved trajectories are quite common, we can see them in the rolling of the wheels of a bicycle, in the movement of the blades of a mill or a fan.
Although we do not see it, we also know that the moon follows a movement in a curved trajectory around the Earth, the planets around the sun, the sun around the Milky Way galaxy, also the movement of electrons around the nucleus of the atom, in short many movements where the curved path is present.
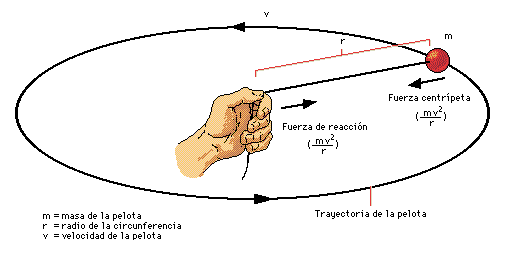
Interactions occurred when a body is rotated.
It is interesting to note that this type of movement is associated with the interaction of one body with another that is fixed and that as a consequence one of these bodies is forced to turn around another.
How does the change in the amount of movement occur due to a centripetal force?
The changes of movement produced by force occur in the direction that this force is applied, considering the mass of the body as constant. (Newton's 2nd law).
Movements involved in circular trajectories in petroleum engineering.
There are many trajectories of movements that occur in drilling operations in an oil location, in this particular case as I am trying circular movement, I want in this case to cite the examples of some operational activities in which some movements are involved. circular:
Movement of the drilling string: this a set of pipes that are threaded each other and which in turn is connected to a rotating joint called the mole drive, the top drive is rotated by the action of the electricity produced by the generators. the location, turning the top drive, turns the string, and within the operational parameters that are recorded are the units of rpm, which means the revolutions per minute, ie for each minute that passes, this has given a considerable amount of revolutions in their turns.
Trajectory that the operators follow when applying moment to tighten the rocks of the pipe: Every time that a pipeline is going to be connected, the drill workers, also called keyholes, connect a hydraulic wrench to screw the pipe. Physically speaking, the force applied by the workers by the radius of action along the key, is what we know as moment or torque, and is equal to the force multiplied by the length of the arm or lever, is measured in Newton by meter. Now many will say and what does a torque have to do with circular motion? It turns out that when the workers when they are tightening or unscrewing a pipe have to follow a circular path through the pipe to apply the correct torque to the pipe, empirically and by experience and the workers know how many turns have to give to apply the torque optimal to the screwing of the pipe, this coupled with that if we take time timed, then we would be talking about revolutions per minute (RPM), and we can also study the geometry involved in the radius of action of rotation that follows the circular path of the workers when they are squeezing.

Please upvote: https://steemit.com/free/@bible.com/4qcr2i
Congratulations @elimao! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The results, the winners and the prizes