Birthday Paradox, Intuitive Explanation

Several years ago, in statistics class, my professor introduced me to the Birthday Paradox, or Birthday Problem. It fascinated me because my lizard brain could not comprehend what was going on. It goes like this, "If there are 23 people in a room, there is slightly over a 50% chance that at least two people will share a birthday." Wow, really? Let me think about this.

There are many posts about this paradox online, including Steemit, but almost all of them explain this phenomenon with fancy math that has exclamation marks where numbers should be. I thought to myself, there must be an intuitive explanation.

The math assumes that there are 365 days in a year, and each person has an equal chance of any given birthday, or 1/365 chance for any given day. Okay, fair enough, but if my birthday is July 20th, then the guy next to me has a 1/365 chance of having the same birthday as me. That is true for everyone in the room, but the paradox states that we have to account for what if Bobby and Amy share a birthday, and Jim and Mary, and Bobby and Mary, etc.

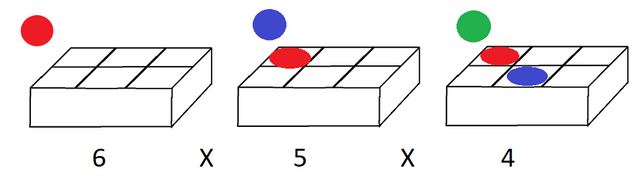
One reason why the birthday problem is so hard to conceptualize is because of the extraneous information. Let's imagine you are at a carnival and there is a game where you throw a ball into a box.

Let's say there is an equal chance (1/6) each time your throw a ball of it landing in any given square in a box of six. If there is a second ball throw (blue), it has a (1/6) chance of landing with the first ball (red).

However, if we introduce a third ball, the probabilities become more complicated to calculate. The green ball has a 2/6 or 1/3 chance of landing with another ball in the combination below on the left, but we also have to account for what if the blue ball already landed with the red ball.

The combination above to the right satisfies the criteria of two balls sharing a square, or two people sharing a birthday, so the game is over. We don't even have to throw the green ball. That is why most explanations or solutions to this paradox choose to take the compliment of the problem. It is much easier to find the odds of no ball sharing a square than at least two balls sharing a square.

First, we have to think about how many possible combinations there are. If there was only 1 ball, then it would be obvious that there are 6 possible combinations. The red ball in each square.

If there are 2 balls, then you have to multiply the 6 squares by 6 more squares, to account for the 2nd ball, or 6 * 6 = 36 possible combinations.

If there are 3 balls and 6 squares, there are 216 possible combinations, or 6 * 6 * 6.

Now, here comes the fun stuff. How many possible combinations are there if no two balls share the same square in a 3 ball, 6 square game? You take the beginning square count 6, multiply that by one minus the beginning square count 5, multiply that by one more minus the beginning square count, 4. Why? Because the first ball has 6 options, the second ball has 5 options, and the third ball has 4 options.

That gives us 120 possible combinations with no two balls in the same square. We divide that by all possible combinations, 216, and we get 55.5%. Wait, we're not done. That is the probability of no two balls in the same square. If we want the probability of at least two balls in the same square, we take the compliment. 100% minus 55.5%, which is 45.5%.

Another way to look at it is on the second frame with the blue ball about to be dropped, you have 5/6 chance of not landing on red. On the third frame, the green ball has a 2/3 chance of not landing on red or blue. We multiply the probabilities, 5/6 * 2/3 to get 55.5%.

Now, back to the Birthday Paradox. Let's apply the same principles but scaled up. There are 23 balls and 365 squares.

Like the ball problem, we will compliment the question. What are the chances of no two people sharing the same birthday? First, total possible combinations of people and their birthdays, 365^23. Or 365 * 365 * 365 *365 * 365 * 365 * 365 *365 * 365 * 365 * 365 *365 * 365 * 365 * 365 *365 * 365 * 365 * 365 *365 * 365 * 365 * 365. If there were only 3 people, or 3 balls, it would be 365 * 365 * 365.

Now, let's take total possible combinations of no two people sharing the same birthday, 365 * 364 * 363 *362 * 361 * 360 * 359 *358 * 357 * 356 * 355 *354 * 353 * 352 * 351 *350 * 349 * 348 * 347 *346 * 345 * 344 * 343 = 365! / (365-23)! I do not know of any calculators that can compute the raw value of that equation.

We divide that by the total possible combinations of 23 people and their birthdays, and we get 49.27%. That is the probability of no two people sharing the same birthday. We take the compliment, 1 - .4927, and we get 0.5073, or 50.73%. And there you go folks, the probability of at least two people sharing the same birthday in a room of 23 people is over 50%.